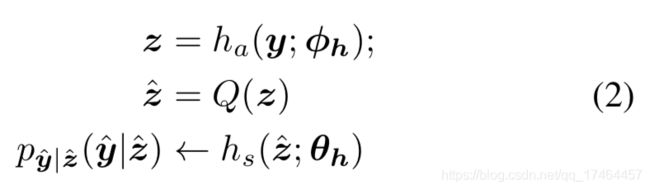图像压缩之《Learned Image Compression with Discretized Gaussian Mixture Likelihoods and Attention Modules》

论文地址： https://arxiv.org/pdf/2002.01657.pdf

代码地址：https://github.com/ZhengxueCheng/Learned-Image-Compression-with-GMM-and-Attention

摘要

现在基于深度学习的图像压缩方法有着快速的发展同时也有着令人满意的结果，但是，在可学习的压缩算法和现行压缩标准之间仍然存在性能差距，尤其是在广泛使用的PSNR度量方面。本文探讨了最近的可学习的图像压缩算法中的存在的冗余问题，作者发现对于率估计，准确的熵模型极大的影响着模型的参数优化，也因此而影响率失真的表现。因此，作者提出使用离散的高斯混合似然来参数化潜在表示的分布，这样可以实现更准确和便捷的熵模型。此外，作者还使用注意力机制来增强模型的表现。实验表明，在PSNR指标上，本方法可以达到VVC(H266)的主帧压缩的表现，更重要的是由MSSSIM优化的模型可以生成视觉效果更好的结果。

本文的主要工作

1. 通过对Balle模型一代(超先验模型Hyperprior，0均值高斯分布)[1]， 二代(联合自回归模型，Joint PixelCNN和非零均值高斯模型)[2]的熵估计的可视化分析，发现虽然二代的熵估计较一代要准确但是仍有明显的冗余，受此启发，作者提出使用离散高斯混合模型来对隐层特征进行熵估计，这样可以实现更准确的熵估计；

2. 通道注意力机制会关注到复杂的区域，也可以提升模型编码性能；

Proposed Method

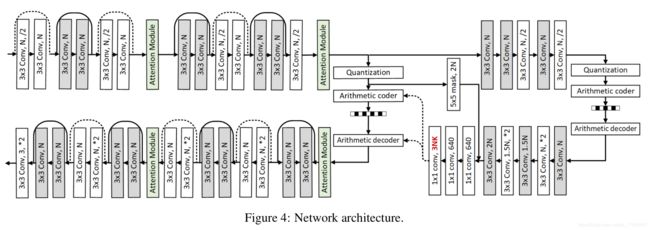
本文提出的离散化高斯混合模型的图像压缩方法的整体网络结构如下图所示：

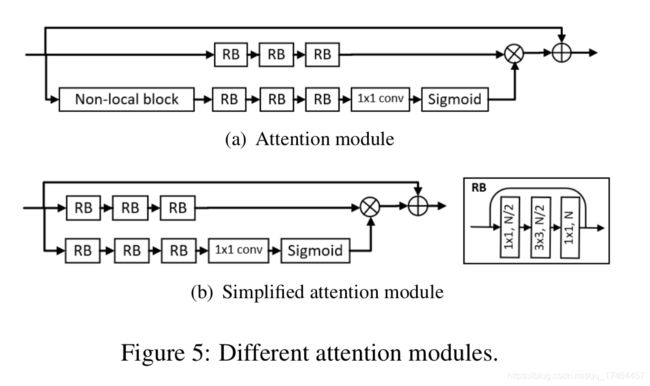
网络结构中的注意力机制模型如下图所示：

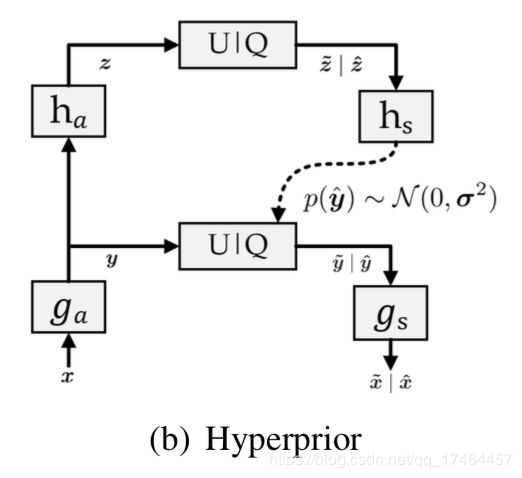
本文从熵估计方面对图像压缩进行分析，发现熵估计对模型的压缩性能影响很大。对于Balle第一代图像压缩方法整体处理流程如下图所示：

熵估计模型的参数化表示如下：

隐层特征y是在z的基础上进行分布估计的，其中y的估计是由一个参数化的0均值，尺度参数为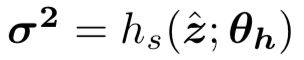的高斯分布进行估计。

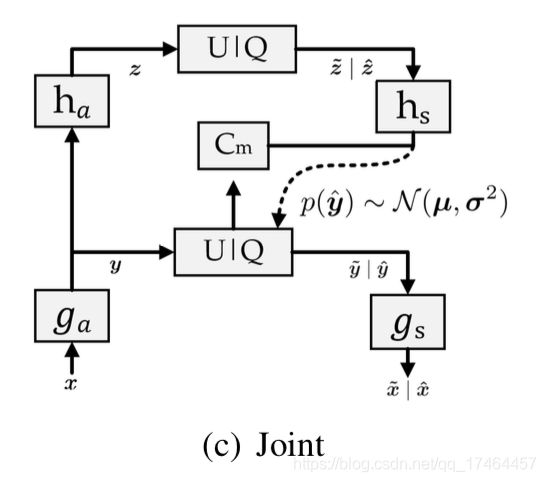
Balle第二代的处理流程如下图所示：

对于熵估计的改进就是将自回归模型(PixelCNN，即图中的Cm)与带有均值与方差的高斯分布联合对隐层特征y进行估计，这样的熵估计相对于第一代要更准确一些，模型的压缩性能也更好；

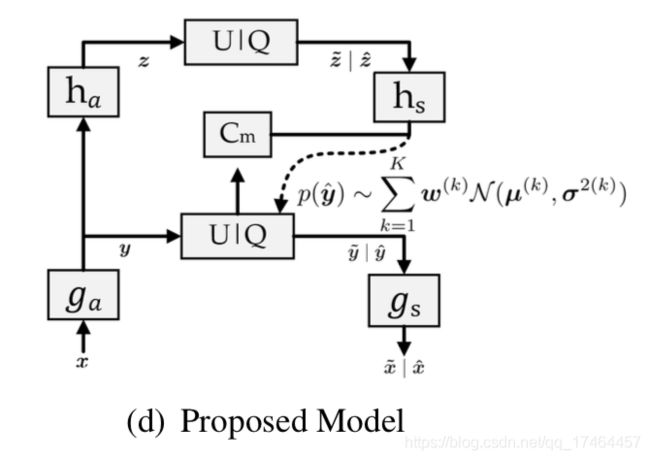
基于对熵估计的分析，可能因为形状固定的单个高斯模型估计隐层特征分布的能力有限，受此启发，作者提出使用离散高斯混合模型进行熵估计，其处理流程如下图所示：

其参数化表示如下：

因为高斯分布是处理连续数值的，但是隐层特征经过量化后是离散的，所以采用离散的高丝混合模型。此外，有研究发现相较于逻辑混合似然，高斯似然效果要稍微更好一些。所以由高斯混合构成的熵模型由下述公式表示：

其中，i表示特征图中的位置，比如表示y的第i个元素， 表示的第i个元素，k表示混合高斯模型的索引。每个高斯模型有三组参数，权重，均值，和方差。实验中，k=3，即使用3个混合高斯模型。在训练中，为了能稳定的训练，将的值截断至[-255,256]之间，因为经验上的值不会超过这个范围。高斯混合模型能够取得更好的性能表现是因为它会选择K最可能的值并且分配小尺度(比如，高似然性)。在一种极端情况下，3个选择的均值相同，此时就会表现的和单高斯模型一样，这会在平滑区域出现；另一种极端情况是3个选择的均值完全不同，这表示模型会有三个似然峰值表示最有可能的值，而这经常出现在边界，边缘或者复杂区域。此外，权重，均值，和方差是针对每一个元素并且均是在训练中可学习的。

实验结果

Hyperprior模型，Joint模型和作者提出的熵估计模型(离散高斯混合模型)的熵估计的可视化结果：

相对于Hyperprior模型，Joint模型，作者的模型熵估计部分的空间冗余更少，即表明估计的更准确。此外作者还在Kodak数据集上进行了测试，PSNR的表现可以与VVC(H66)主帧压缩的性能相匹敌了，本文模型的结果已经远超BPG(H265的主帧压缩算法)了并且达到了最新的压缩性能，具体结果如下图：

 

参考文献

[1] Johannes Balle, D. Minnen, S. Singh, S. J. Hwang, N. John- ston, “Variational Image Compression with a Hyperprior”, Intl. Conf. on Learning Representations (ICLR), pp. 1-23, 2018.

[2] D. Minnen, J. Balle ́, G. Toderici, “Joint Autoregressive and Hierarchical Priors for Learned Image Compression”, NIPS2018.