20200417:力扣147周赛题解
力扣147周赛题解
- 题目
- 思路与算法
- 代码实现
- 复杂度分析
题目
1. 第N个泰波那契数
思路与算法
-
第一题没有什么难度,直接递归会超时,由于结果小于2^32-1,所以n最大为37,因此直接计算出这38个值的结果存入数组,最后直接输出即可。
-
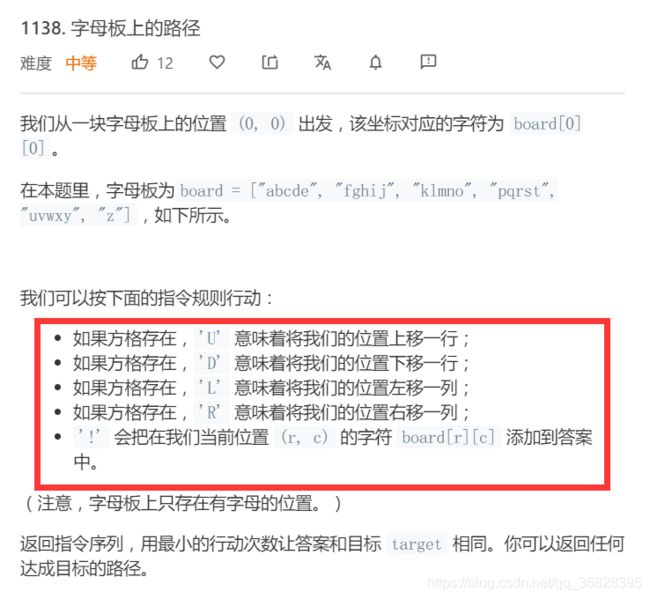
第二题主要的难点在于如何把字母与board上的位置对应起来,实际上也不难,我们只需要让每一个字母减去‘a’获取到0-25这26个数字来对应26个英文字母即可,每个数字除以5代表当前字母所在的行0-5,对5求余代表当前字母所在的列0-4,对应26个英文字母,至此,完成接下来的代码即可。
-
第三题是一个典型的动态规划问题,我们可以从右下角开始记录当前位置所在的行和列对应存在的最多的连续的1的个数,使用三维数组的第三维度来存放即可。如果最终构成一个正方形的1,则对应的dp数组的该正方形的左上角,左下角,右上角对应的行列存储的最大1的个数应该都至少>=n,而这个n就是我们最终求解的正方形的边长。
-
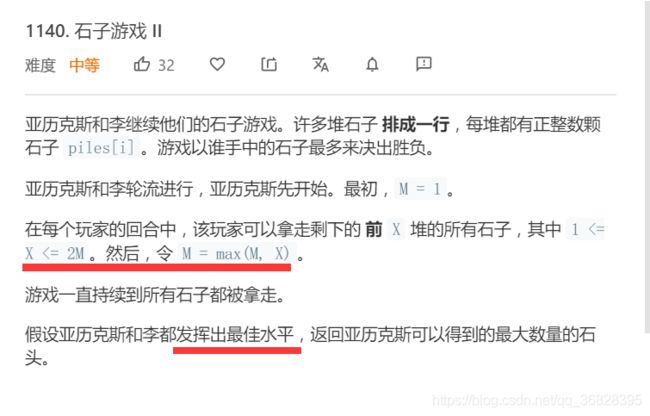
第四题是一个典型的dfs解决的问题,除了当前的数组还需要两个输入变量,一个起始索引一个起始能力值M=1。使用正常的计划递归和动态规划都可以完成本题的解答。两种写法也都列在代码中,以供后续复习。
代码实现
1. 第N个泰波那契数
class Solution {
public int tribonacci(int n) {
int[] res = new int[38];
res[0] = 0;
res[1] = 1;
res[2] = 1;
for (int i = 3; i <= n; i++){
res[i] = res[i-1] + res[i-2] + res[i-3];
}
return res[n];
}
}
2. 字母板上的路径
class Solution {
public String alphabetBoardPath(String target) {
// 从四个方向直接找即可
int X = 0;
int Y = 0;
int curX = 0;
int curY = 0;
StringBuilder res = new StringBuilder();
for (int i = 0; i < target.length(); i++){
// 获取当前字母对应的字母表序号
int tmp = target.charAt(i) - 'a';
if( i > 0 && target.charAt(i) == target.charAt(i-1)){
res.append("!");
} else{
// 计算当前字母在board的第几行第几列
curX = tmp / 5; // 行
curY = tmp % 5; // 列
// 必须先左上,后右下
if( curY < Y ){
for( int j = 0; j < Y - curY; j++)
res.append("L");
}
if( curX < X ){
for( int j = 0; j < X - curX; j++)
res.append("U");
}
if( curY > Y ){
for( int j = 0; j < curY - Y; j++)
res.append("R");
}
if( curX > X ){
for(int j = 0; j < curX - X; j++)
res.append("D");
}
res.append("!");
X = curX;
Y = curY;
}
}
return res.toString();
}
}
3. 最大的以 1 为边界的正方形
class Solution {
public int largest1BorderedSquare(int[][] grid) {
if (grid.length == 0){
return 0;
}
// 获取高度和宽度
int height = grid.length;
int width = grid[0].length;
// 定义dp数组,用于记录坐标处对应的上边的1的个数和左边的1的个数
int[][][] dp = new int[height+1][width+1][2];
// 逐个记录
for (int i = height-1; i >= 0; i--){
for (int j = width - 1; j >= 0; j--){
if ( grid[i][j] == 1){
// 更新对应的dp数组的值
// 左边
dp[i][j][0] = dp[i][j+1][0] + 1;
// 上边
dp[i][j][1] = dp[i+1][j][1] + 1;
}
}
}
// 进行判断是否为最大边长即可
int len = Math.min(height,width);
while (len > 0){
for (int k = 0; k < height - len; k++){
for (int l = 0; l < width - len; l++){
if( dp[k][l][0] >= len && dp[k][l][1] >= len && dp[k + len + 1][l][0] >= len && dp[k][l - len + 1][1] >= len){
return len * len;
}
}
}
}
return 0;
}
}
4.石子游戏 II 自顶向下的计划递归写法
package com.immunize.leetcode.week147;
public class Solution {
private int[] suffixSum;
private int[][] dp;
public int stoneGameII(int[] piles) {
// 如果数组为空,则返回0
if (piles == null || piles.length == 0)
return 0;
// 数组长度n
int n = piles.length;
// 新建前缀和数组
suffixSum = new int[n];
suffixSum[n - 1] = piles[n - 1];
// 初始化前缀和数组
for (int i = n - 2; i >= 0; i--) {
suffixSum[i] = suffixSum[i + 1] + piles[i];
}
// 新建dp数组
dp = new int[n][n];
return findMaxStones(piles, 0, 1);
}
private int findMaxStones(int[] piles, int i, int M) {
// 特殊情况处理
if (i == piles.length)
return 0;
if (i + 2 * M >= piles.length) {
return suffixSum[i];
}
if (dp[i][M] != 0)
return dp[i][M];
int minStones = Integer.MAX_VALUE;
for (int X = 1; X <= 2 * M; X++) {
// Lee可以获得的最小石子数,即可获得Alex获得的最大石子数
minStones = Math.min(minStones, findMaxStones(piles, i + X, Math.max(X, M)));
}
dp[i][M] = suffixSum[i] - minStones;
return dp[i][M];
}
}
4.石子游戏 II 自底向上的动态规划写法
class Solution {
public int stoneGameII(int[] piles) {
int len = piles.length;
int sum = 0;
int[][] dp = new int[len + 1][len + 1];
int[] acum = new int[len + 1];
for (int j = 0; j < len; j++){
acum[j + 1] = acum[j] + piles[j];
}
for (int i = len - 1; i >= 0; i--) {
for (int M = 1; M <= len || M == 1; M++) {
for (int x = 1; x <= 2 * M; x++) {
if (i + x - 1 > len - 1) {
break;
}else{
dp[i][M] = Math.max(dp[i][M], acum[len] - acum[i] - dp[i + x][Math.max(M, x)]);
}
}
}
}
return dp[0][1];
}
}
复杂度分析
周赛复杂度特殊的会分析,一般的更加关注算法本身。