20200729:力扣199周周赛题解(下)
力扣199周周赛题解(下)
题目三:好叶子节点对的数量
- 给你二叉树的根节点 root 和一个整数 distance 。
- 如果二叉树中两个叶节点之间的 最短路径长度 小于或者等于 distance ,那它们就可以构成一组 好叶子节点对 。
- 返回树中 好叶子节点对 的数量 。
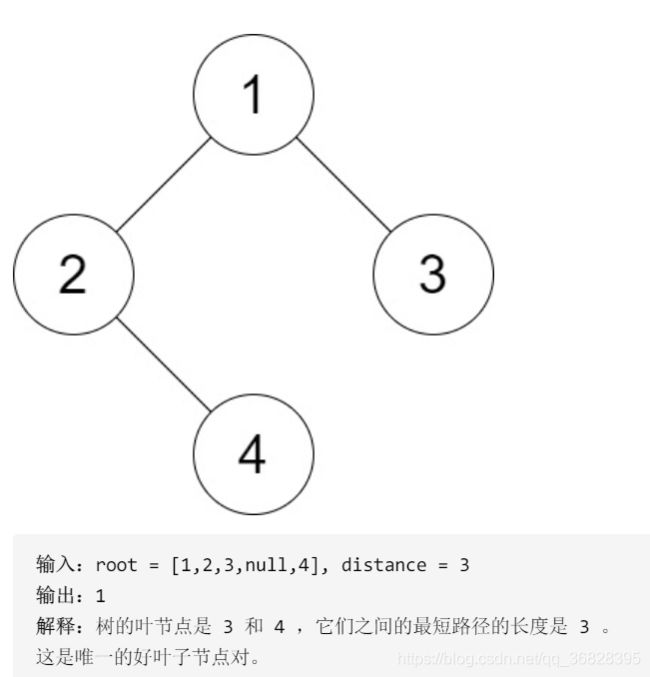
示例
解题思路
遍历获取每个节点到其下方所有叶子节点的距离记录为list,left为左子树的list,right为右子树中离叶子节点的list值,找到左右距离之和小于distance的即为满足条件的,返回即可。
代码实现
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int ans=0;
public int countPairs(TreeNode root, int distance) {
dfs(root,distance);
return ans;
}
private List<Integer> dfs(TreeNode root,int distance) {
// 特殊情况处理
if (root == null) {
return new ArrayList();
}
if(root.left==null&&root.right==null){
return new ArrayList().add(0);
}
// 初始化结果list
List<Integer> list=new ArrayList();
// 分别记录当前节点下其左右子树下的叶子节点到当前节点的长度,存入left和right两个list
List<Integer> left=dfs(root.left,distance);
for(int it:left){
if (it + 1 <= distance) {
list.add(it+1);
}
}
List<Integer> right = dfs (root.right,distance);
for (int it:right) {
if (it + 1 <= distance) {
list.add(it+1);
}
}
for(int l:left){
for(int r:right){
if(l+r+1 < distance)
ans++;
}
}
// 返回
return list;
}
}
题目四: 压缩字符串 II
行程长度编码 是一种常用的字符串压缩方法,它将连续的相同字符(重复 2 次或更多次)替换为字符和表示字符计数的数字(行程长度)。例如,用此方法压缩字符串 “aabccc” ,将 “aa” 替换为 “a2” ,“ccc” 替换为` “c3” 。因此压缩后的字符串变为 “a2bc3” 。
注意,本问题中,压缩时没有在单个字符后附加计数 ‘1’ 。
给你一个字符串 s 和一个整数 k 。你需要从字符串 s 中删除最多 k 个字符,以使 s 的行程长度编码长度最小。
请你返回删除最多 k 个字符后,s 行程长度编码的最小长度 。
代码实现
代码转自@kwantong大佬,时间有限,我未能理解到位,明天再补上马后炮解题思路
class Solution {
public int getLengthOfOptimalCompression(String s, int k) {
int n = s.length();
int[][] dp = new int[n + 1][k + 1];
// dp[i][j]: 前i个数,删减j次,最短长度
for (int i = 0; i < n + 1; i++) {
Arrays.fill(dp[i], n);
}
dp[0][0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= k; j++) {
int same = 0;
int delete = 0;
// 情况一,保留s[i-1],同时删掉s[0...i-1]跟s[i-1]不同的
for (int l = i; l >= 1; l--) {
if (s.charAt(l - 1) == s.charAt(i - 1)) {
same++;
} else {
delete++;
}
if (j - delete >= 0) {
// 够余额去删,长度为:s[0...l-2]最好的结果,并上s[l-1...i]中same个s[i-1]
dp[i][j] = Math.min(dp[i][j], dp[l - 1][j - delete] + getDigits(same) + 1);
}
}
// 情况二,删掉s[i-1]
if (j >= 1) {
dp[i][j] = Math.min(dp[i][j], dp[i-1][j-1]);
}
}
}
return dp[n][k];
}
private int getDigits(int n) {
if (n == 1) {
return 0;
}
if (n > 1 && n < 10) {
return 1;
}
if (n >= 10 && n < 100) {
return 2;
}
return 3;
}
}