路由选择算法——链路状态算法
好久没写东西了,好生疏的感觉。。
链路状态算法
这是一种全局式的路由选择算法,也就是说,一个路由器知道到其他路由器的所有链路的状态信息(例如某条链路上堵不堵),并且假设这种信息是被量化好了的(以拥堵情况为例,越拥堵该值越大),在这样的情况下,链路状态算法就是要让路由器在这些链路中选择一条最好的从源到目的主机的路径。什么是最好?当然是路径上所有链路的状态加起来最好(拥堵度最小)。
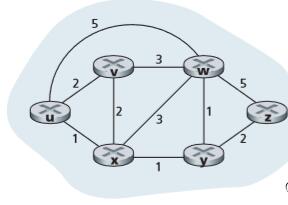
假设上图中的数字代表拥堵状态(值越大,越拥堵)。路由选择后,除去那些无关的边,可以得到以下的结果:
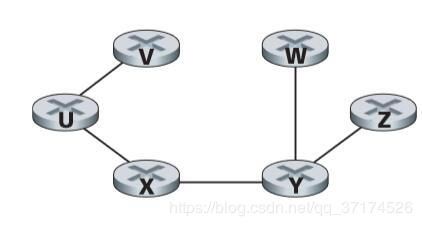
其实这就是在一个图里面选最短路径的算法,so,Dijkstra算法搞起,这里先作以下约定:
D(v):表示从源节点到目标结点v的最优路径的cost
p(x):从源结点到目标节点v(最低cost路径)的前一个结点(v的邻居)
N':如果从源到v的最低cost路径已知,那么可以将v加入N'集合中 (代码里面我用N_fnd表示)
w:可被加入到N' 中结点,且节点的cost最小 (代码中我用minimum_idx表示)
算法伪代码
1、初始化:
N' = {u}
for all nodes for n
if n is a neighbor of u
then D(n) = c(u,n)
else D(n) = ∞
2、循环阶段
find w not in N' such that D(w) is a minimum
add w to N'
update D(n) for each neighbor n of w and not in N'
D(n) = min( D(n) , D(w)+c(w,n) )
until N' = N
Code (Python version)
# dijkstra for Link State Algorithm
import numpy as np
def generate_instance():
# 各点下标为 u-0,v-1,w-2,x-3,y-4,z-5,
idx_map = {0: 'u', 1: 'v', 2: 'w', 3: 'x', 4: 'y', 5: 'z'}
# 为了方便,我把无穷大定义为了9999
c = np.zeros((6, 6), dtype=int)
c[0][0] = 0
c[0][1] = c[1][0] = 2 # u,v,2
c[0][2] = c[2][0] = 5 # u,w,5
c[0][3] = c[3][0] = 1 # u,x,1
c[0][4] = c[4][0] = 9999
c[0][5] = c[5][0] = 9999
c[1][1] = 0
c[1][2] = c[2][1] = 3 # v,w,3
c[1][3] = c[3][1] = 2 # v,x,2
c[1][4] = c[4][1] = 9999
c[1][5] = c[5][1] = 9999
c[2][2] = 0
c[2][3] = c[3][2] = 3 # w,x,3
c[2][4] = c[4][2] = 1 # w,y,1
c[2][5] = c[5][2] = 5 # w,z,5
c[3][3] = 0
c[3][4] = c[4][3] = 1 # x,y,1
c[3][5] = c[5][3] = 9999
c[4][4] = 0
c[4][5] = c[5][4] = 2 # y,z,2
c[5][5] = 0
return c, idx_map
def LS_algorithm(c):
"""
:param c: 邻接矩阵
"""
# step1:初始化
# 已经确定的点
N_fnd = [False for i in range(len(c))]
N_fnd[0] = True
# p(v) 从源点到目标节点v最小路径中的前一个点
p = [0 for i in range(len(c))]
# 当前状态下,源点到各点的距离
D = c[0]
# step2. 循环阶段
for i in range(len(D)):
# 找出c向量中的最下值和对应那个点的下标
minimum = 10000
minimum_idx = -1
for j in range(len(c)):
if D[j] < minimum and not N_fnd[j]:
minimum = D[j]
minimum_idx = j
N_fnd[minimum_idx] = True
# 然后看是否存在使得通过该点“中转”使得源点能最小到的点
for idx in range(len(D)):
# 中转之后比原来还小
if D[minimum_idx] + c[minimum_idx][idx] < D[idx]:
D[idx] = D[minimum_idx] + c[minimum_idx][idx]
p[idx] = minimum_idx
return D, p
def print_route(D, p):
# 打印出最短路径
for i in range(len(D)):
print("从源点到目标点%s的最短路径为%d" % (idx_map[i], D[i]))
route_prefix = "具体路径为:u"
# 从后向前倒着输出
route = "-->%s" % (idx_map[i])
out_node_idx = i
while True:
# 到了源点
if p[out_node_idx] == 0:
break
route = "-->%s" % (idx_map[p[out_node_idx]]) + route
out_node_idx = p[out_node_idx]
print(route_prefix + route)
if __name__ == '__main__':
c, idx_map = generate_instance()
D, p = LS_algorithm(c)
print_route(D, p)
输出
从源点到目标点u的最短路径为0
具体路径为:u-->u
从源点到目标点v的最短路径为2
具体路径为:u-->v
从源点到目标点w的最短路径为3
具体路径为:u-->x-->y-->w
从源点到目标点x的最短路径为1
具体路径为:u-->x
从源点到目标点y的最短路径为2
具体路径为:u-->x-->y
从源点到目标点z的最短路径为4
具体路径为:u-->x-->y-->z