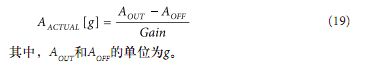加速度计

加速度计原理：

   加速度传感器实际上是用MEMS技术检测惯性力造成的微小形变，把加速度传感器水平静止放在桌子上，它的Z轴输出的是1g的加速度。因为它Z轴方向被重力向下拉出了一个形变。可惜的是，加速度传感器不会区分重力加速度与外力加速度。所以，当系统在三维空间做变速运动时，它的输出就不正确了，或者说它的输出不能表明物体的姿态和运动状态。

加速度传感器有什么用？ 加速度计,可以测量加速度,包括重力加速度,于是在静止或匀速运动（匀速直线运动）的时候,加速度计仅仅测量的是重力加速度,而重力加速度与刚才所说的R坐标系（绝对坐标系）是固连的,通过这种关系,可以得到加速度计所在平面与地面 的角度关系 也就是横滚角和俯仰角。

规范化四元数作用：

   表征旋转的四元数应该是规范化的四元数，但是由于计算误差等因素，计算过程中四元数会逐渐失去规范化特性，因此必须对四元数做规范化处理。

   由于误差的引入，使得计算的变换四元数的模不再等于1，变换四元数失去规范性，因此再次更新四元数后，需要对四元数做规范化处理。

   重力加速度归一化：把加速度计的三维向量转换为单位向量， 因为是单位矢量到参考轴的投影，所以要把加速度计数据单位化，其实归一化改变的只是这三个向量的长度，也就是只改变了相同的倍数，方向并没有改变，也是为了与单位四元数对应。

   将当前姿态的重力在三个轴上的分量分离出来，把四元数换算成方向余弦中的第三行的三个元素，根据余弦矩阵和欧拉角的定义，就是地理坐标系（参考坐标系）的Z轴的重力向量。

   四元数矩阵，转置之后可以获得下面的 M 矩阵；所以 M13与四元数矩阵的 Q31元素等价，M23与四元数矩阵的Q32元素等价。 当处理磁力计时，当不考虑外界干扰磁场时，地球磁场的分量为 | Mx 0 My | 在东向的磁场分量为0（北半球，磁场分量指向 北 和 垂直地面）。。。当考虑外界干扰时，为 | Mx My Mz |。。。

   由四元数获得的旋转矩阵是固定的；由欧拉角旋转获得的矩阵，会因为旋转顺序的不同，而获得不同的矩阵形式；当小角度旋转时，可以忽略旋转顺序不同而产生的误差。当旋转顺序确定之后，两个旋转矩阵可以通过相互转置而获得等价关系。

摘自 ANALOG DEVICES AN-1057应用笔记

简介

   确定系统倾斜的一种常用方法是对陀螺仪输出求积分。尽管这种方法简单明了，但随着积分周期的增加，与零偏稳定性相关的误差也可能快速增大，即使当器件处于静止状态时也可能导致明显的旋转。

   在某些净加速度或重力加速度的应用中，可利用加速度计来测量静态倾斜角。此类应用包括游戏，数码相机水平检测，以及工业和医学应用中检测器件方向等。

   利用加速度计进行倾斜检测的基本假设是，加速度只与重力相关。实际上，可对信号输出进行信号处理，以消除其中的高频组分，因而可以接受一定的交流加速度。

   由于重力为直流加速度，因此，任何额外加入的直流加速度都会破坏输出信号并导致错误计算。造成直流加速度的因素包括车辆以恒定速率加速时的时间，以及在加速度计上导致向心加速度的旋转器件。在计算倾斜之前对加速度信号进行的任何过滤都会影响输出达到新静态值的速度。

倾斜计算

单轴倾斜计算

   在重力为理想值1 g时，输出加速度为AX.OUT[g] = 1 g * sin(θ) (1)

   采用单轴解决方案时，随着水平线与x轴夹角的增大，倾斜计算的灵敏度——即一定输入变化带来的输出变化——会变小，该角越接近±90°，灵敏度越接近0（由正弦函数性质决定）。从图2即可看出这点，图中，输出加速度（单位：g）相对于倾斜角。接近±90°时，倾斜角的较大变化会导致输出加速度发生小幅变化。

   由于倾斜计算以数字方式实现，所以输出加速度表示为单位最低有效位（LSB）的一个恒定加速度或代码，该值来自模数转换器（ADC）或直接来自数字输出部件。由于输出分辨率为恒定加速度，因此倾斜角度分辨率是可变的，其中，其中，最佳分辨率在接近0°时取得，最差分辨率在±90°时获得。

   图3和图4分别为1°和0.25°倾斜角步进下的增量灵敏度。增量灵敏度为单位倾斜角步进的输出变化（单位：mg），或

S[g] = lg*( sin(N+P) - sin(N) ) (2) 其中： N为初始角度。 P为步长。

   在测量输出加速度时，可利用这个曲线来确定要求的最低分辨率，以满足具体应用整个范围的倾斜分辨率要求。例如，对于1°的最大步长，±63°范围至少需要8 mg/LSB的分辨率。类似地，在±63°的范围内，如果要获得0.25°的最大步长，则需要至少2 mg/LSB的分辨率。注意，如果存在大量的扰动，则可借助过采样来取得更好的分辨率。

由于通过重力旋转时，加速度计的输出遵循一种正弦关系，因而通过反正弦函数来实现从加速度到角度的转换。

   (3)

其中，倾斜角θ单位为弧度。如果所需倾斜范围较窄，则可用线性逼近法代替反正弦函数。线性逼近法实为逼近小角度的正弦。

   (4)

其中，倾斜角θ单位为弧度。 可在倾斜角的线性逼近公式中增加比例因子k，以便在可容忍误差加大时，增加逼近法的有效范围。

(5)

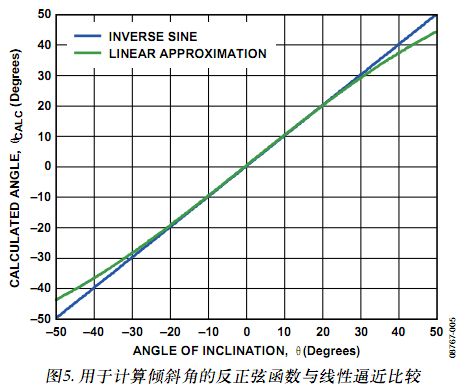
其中，倾斜角θ单位为弧度。将等式5所得结果乘以（180/π），即可得到角度数。图5比较了反正弦函数和线性逼近法（其中k=1）的结果。随着倾斜角度的加大，线性逼近法逐渐失效，计算所得角度开始偏离实际角度。

由于算出的角度在坐标图上以实际倾斜角为参照，因而，在两端，线性逼近法存在一定弯曲。这是因为仅当与输出加速度相比较时，线性逼近才呈线性，随着实际倾斜角的加大，输出加速度具有类似表现（如图2所示）。然而，反正弦函数产生的输出与实际倾斜角成一比一关系，当以实际倾斜角为参照时，会使计算角度表现为一条直线。

举例来说，如果倾斜检测的目标分辨率为1°，则±0.5°的误差处于可接受水平，因为该误差值低于计算的舍入误差。如果对实际倾斜角与计算倾斜角的误差作图，且k=1，如图6所示，则线性逼近法的有效范围仅为±20°。如果调整比例因子以使误差最大但仍处于计算舍入限值以内，则线性逼近法的有效范围将加大至大于±30°的水平。

双轴倾斜计算

单轴倾斜检测的一种不足在于，需要采用高分辨率ADC或数字输出，才能获得大范围的有效倾斜角，分别如图3和图4所示。另一种缺陷是，单轴检测无法提供360°测量，因为倾斜角N°下产生的加速度等于倾斜角180°-N°下产生的加速度。对于某些应用，这是可以接受的，但对于要求较高分辨率的应用，或者需要区分整个360°弧内的不同倾斜角，则需要第二个轴（如图7所示）或第二个传感器。在采用第二个传感器的情况下，该传感器必须方向正确，使其检测轴与第一个传感器的检测轴垂直。

确定倾斜角时采用第二个周，这种做法有三个主要优势。

恒定灵敏度

采用第二个轴的首要优势来自两轴的垂直关系。与单轴解决方案一样，x轴检测到的加速度与倾斜角的正弦具有比例关系。同时与x轴垂直的y轴加速度与倾斜角的余弦成比例（见图8）。随着某个轴的增量灵敏度的降低，比如该轴上的加速度接近+1 g或 -1 g时，另一个轴的增量灵敏度会增加。

将测得加速度转换成倾斜角的一种方法是计算x轴的反正弦及y轴的反余弦，与单轴解决方案类似。然而，一种更简单、更有效的方法是使用来自以下等式的两个值之比：

   (6)

   (7)

其中，倾斜角θ单位为弧度。

不同于单轴示例，利用两个轴之比来确定倾斜角的方法极大地增加了确定增量灵敏度的难度。相反，在给定倾斜分辨率的条件下，确定加速度计的最低必要分辨率显得更为有用。由于一个轴的增量灵敏度会随着另一轴的减少而增加，因此两者的最终结果是一种几乎恒定的有效增量灵敏度。这就是说，加速度计的分辨率只要可以在特定角度下实现目标倾斜步长，这样的加速度计可以测量所有角度。

为了确定加速度计所需的最低分辨率，我们考察了等式6，以确定分辨率存在哪些局限性。由于各轴的输出取决于倾斜角的正弦或余弦，且各函数的倾斜角相等，因而，最小可解析角等于最低可解析加速度。

如图3和图4所示，正弦函数在接近0°时变化率最大，不难证明，余弦函数在该点具有最小变化率。为此，由倾斜变化导致的x轴加速度变化可先于y轴加速度变化识别出来。如此一来，系统接近0°时的分辨率主要取决于x轴的分辨率。若要检测到等于P°的倾斜变化，加速度计必须能够检测到的变化约等于：

   (8)

图9可用于确定在目标倾斜步长时，加速度计所需的最低分辨率——或加速度计的最大比例因子。请注意，增加的加速度计分辨率取决于加速度计比例因子的减少量，以及检测输出加速度较小变化的能力。因此，在选择具有适合分辨率的加速度计时，对于目标倾斜步长，比例因子应小于图9所示限值。

对重心面对齐度的依赖性降低

使用双轴或多轴的第二个重要优势在于，在单轴解决方案下，除x轴以外的任何轴发生倾斜都会造成重大误差，与此不同，在使用第二轴时，即使第三轴存在倾斜时也可测得精确的值。这是因为有效增量灵敏度与目标重力的和方根（RSS）值具有比例关系。 （总的增量值与重力的和方根是比例关系）。

当重力完全处于xy平面之内时，这些轴上检测到的加速度方和根的理想值等于1 g。如果xz平面或yz平面中存在倾斜，则重力导致的总加速度会减少，同时会减少有效增量灵敏度（（有效增量灵敏度减小相当于将分辨率进行放大，所以会对应更大的倾斜步长））。这又会加大既定加速度计分辨率下的倾斜步长（（先将重力在倾斜后的平面上进行分解，那么分解量是一定的。）），但仍可提供精确的测量值。经倾斜计算得到的角度对应于xy平面的旋转。

如果系统倾斜角度足够大，以致于xy平面中仅存在极少重力导致的加速度，则倾斜角步长的准确度不够，无法使用；因此建议对xz平面或yz平面中的倾斜进行限制。

全角度360°倾斜检测

采用第二轴的第三个主要优势是能够对各个象限进行区分，并能在整个360°弧度内测量角度。

三轴倾斜计算

引入第三轴时，可以在全球面范围确定传感器的方向。可通过传统的直角坐标（x,y,z）-球面（ρ,θ,φ）转换法来表征xy平面倾斜角θ及重力矢量倾斜角φ

失调和灵敏度失配误差校准

   本应用笔记中的分析假设采用理想加速度计。该假设等同于使用无0 g失调且具有完美灵敏度的器件——灵敏度以mV/g(模拟传感器)或LSB/g(数字传感器)表示。虽然传感器经过调节，但器件本质上是机械的，这便意味着系统完成装配后，器件上的任何静态应力都有可能影响失调和灵敏度。再加上工厂校准的限制，便有可能使误差超出应用允许的限值以外。

失调误差的影响

   为了表明误差到底有多大，可以设想一下，某个双轴解决方案具有完美的灵敏度，但x轴上存在50 mg失调。0°时，x轴读数为50 mg，y轴读数则为1 g。由此计算得出的角度就是2.9°，因而会造成2.9°（用反正切计算 arctan（0.05/1）的误差。±180°时，x轴的读数为50 mg，y轴的读数则为−1 g。由此计算得出的角度会存在−2.9°的误差。图13所示为本例中算出的角度和实际角度之间的误差情况。失调引起的误差可能不仅大于系统所需的精度，而且还会发生变化，使简单地通过校准消除误差角变得困难。当多个轴上都

存在失调时，这将会变得更为复杂。

灵敏度失配误差的影响

   在双轴倾斜检测应用中，由加速度计灵敏度导致的主要误差成分是目标轴之间的灵敏度差异(在单轴解决方案中，如果实际灵敏度和预期灵敏度之间存在任何偏差，则会导致
出现误差)。由于使用的是x和y轴的比值，因此如果两者灵敏度相同，则可以消除大多数误差。

   下面举例说明加速度计灵敏度失配的影响。假设某个双轴解决方案具有完美的失调调整功能，且y轴具有完美的灵敏度，但x轴的灵敏度为+5%。这表示在1 g场中，y轴读数为
1 g，x轴读数则为1.05 g。图14所示为因为这种灵敏度失配而造成角度计算出现的误差情况。与失调误差类似，加速度计灵敏度失配引起的误差会在整个旋转范围内不断变化，
使在计算出倾斜角后进行误差补偿变得困难。改变y轴的灵敏度会进一步增加失配，从而使误差更大。

基本校准技术

当失调引起的误差和灵敏度失配引起的误差两者相叠加时，误差可能会变得相当大，完全超出倾斜检测应用所能接受的范围。要减少这类误差，就应当对失调和灵敏度进行校准，并使用校准后的输出加速度来计算倾斜角。包括失调和灵敏度的影响后，加速度计输出变化如下：

AOUT [g] = AOFF + (Gain × AACTUAL)
(14)
其中： AOFF表示失调误差，单位为g。 Gain表示加速度计的增益，理想值为1。

AACTUAL表示加速度计的真实加速度和目标值，单位为g。

   一种简单的校准方法是假设增益为1并测量失调。经过此校准之后，系统的精度即会限制为未校准的灵敏度误差。这种简单的校准方法可通过将目标轴置于0 g场中并测量输
出(大小等于失调)来完成。然后，应在处理信号之前从加速度计的输出中减去该值。这种方法通常称为无调头或单点校准，因为器件的典型取向会将x和y轴置于0 g场中。如果使用的是三轴器件，则应针对z轴包含至少一个调头或第二个点。一种更加精确的校准方法是每个目标轴上取用两个点(三轴设计最多可取用六个点)。当某个轴处于+1 g和−1 g场中时，测得的输出如下：

   其中，+1 g和−1 g测量结果A+1g和A−1g均以g表示。
   由于测量目标轴时，正交轴都处于0 g场，因此这种校准方法还有助于将跨轴灵敏度影响降至最低。利用这些值，首先可以从加速度计测量结果中减去失调，然后将所得结果除以增益。

   等式15至等式19中，计算AOFF和增益时，假设加速度值A+1g和A−1g均以g表示。如果加速度单位采用mg，则等式17中AOFF的计算结果会保持不变，但等式18中增益的计算结果需要除以1000，以处理单位上的变化。

   这个计算等式说明是相较于传感器的xyz平面的，当使用xy两个轴进行倾斜检测时，如果z轴发生了倾斜，那么检测倾斜的水平面就发生了小幅度的偏转，如果倾斜角度特别小，仍能够保持测量的准确；如果倾斜角度过大，那么测量结果将偏差很多。

---

原文首发于同名微信公号「Allen5G」，欢迎大家搜索关注！

技术交流群：736386324
个人微信：coderAllen（备注读者）