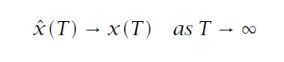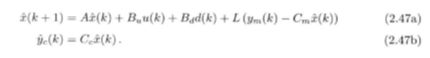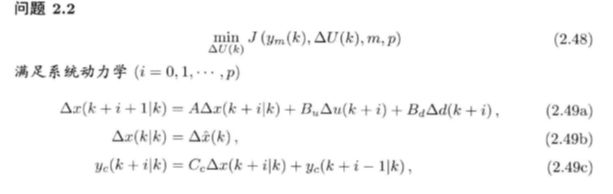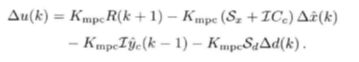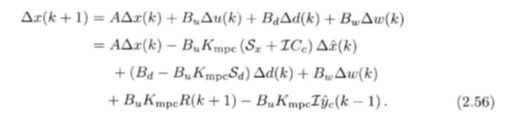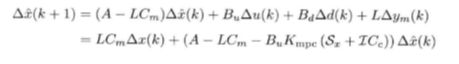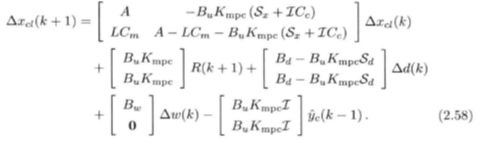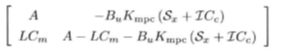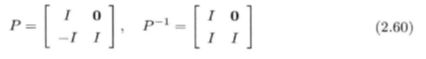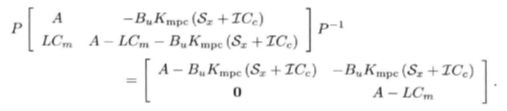基于估计的无约束预测控制
1.引言
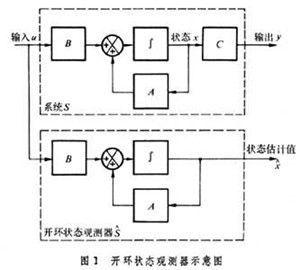
基本上这两个部分都是在线性理论的框架下,利用状态空间法来建模、求解控制律。状态空间模型在理论分析上具有很强的优越性,但实际应用中能直接准确且经济地获取系统状态并不容易。有些状态,尤其是温度(如火箭喷口温度等)只能间接估计,因此我们可以使用状态观测器来重构一个易于实现的系统来模拟原系统的状态。
具体的做法是,先利用原系统可以测量的变量,如系统可测输入输出,使得在一定条件下满足估计的状态与原状态渐进等价,随后利用观测器重构的系统设计控制律。
观测器收敛条件
在设计观测器的时候,首先要判断是否存在观测器。这里以全维观测器为例,观测器重构系统与原系统维度相同。设系统可测量输出为:
设计如下估计器:
若估计器的矩阵对(A,Cm)可测,即全部不能观阵型稳定,则状态观测器存在,可以通过设计L矩阵使(A-LCm)渐进稳定来达到观测器收敛条件。进一步,若(A,Cm)能观,即全部模态在输出端可测,还可以通过设计L任意配置(A-LCm)的极点来控制估计误差的衰减速度,道理和任意配置系统极点设计状态反馈控制器是一样的,两个问题是对偶关系。
2.算法设计
基于估计的算法和原算法基本相同,只是能利用的只有测量值ym和估计值。在预测过程中,用估计值作为预测系统未来状态的起点:
得到的预测方程、控制律均与之前相同:
![]()
![]()
![]()
Ep用到的是估计值,估计值是由测量值代入估计器公式得到。而估计的状态又带入Yp与参考R做平方差形成MSE误差当作待优化值,因此一定要保证L的设计良好才可以实现算法。
3.闭环系统分析
仅对稳定性进行分析,其余包括抗干扰性能和无静差跟踪性能与无约束预测控制相同。
考虑可测和不可测误差,被控系统如下:
这里已经将Δu(k)带入,注意这里是原系统,我们用由估计器设计出来的控制律作用到了原系统上(估计器只是为了模拟原系统行为来获得原来很难获得的状态)。而且,在引入了估计器之后,系统变得更加复杂了,基于估计设计的控制律能否控制原系统,新的系统能否稳定都是需要分析的。
将ym(k)=Cmx(k)和控制律带入估计器:
现在重新定义带状态观测器系统的状态向量:
则:
新的系统矩阵为:
为了满足控制系统设计的基本要求,即名义渐进稳定。我们必须设计控制器让一个标称系统在控制输入的作用下渐进稳定。标称系统(也叫名义系统)是没有任何外部扰动和模型失配的理想系统,与名义稳定相对的是鲁棒稳定。要达到名义稳定需要让这个新的系统矩阵的所有特征根的模长小于一。我们需要验证这个无约束MPC闭环系统是否满足分离原理。
我们希望能将系统满足分离原理,这样意味着闭环系统的极点由原系统在控制律作用下的极点和估计器的极点组成,状态观测器(估计器)的引入对原系统在控制律作用下的极点不影响,这样就可以分别独立设计两个系统的极点。只要两个子系统的极点都达到稳定要求,整合起来的新系统也满足稳定要求。
按道理来讲,基于观测器反馈控制的线性系统是满足分离原理的。之前我们得到的MPC控制律也可以看作一种状态反馈控制律,现在来验证一下是否真的满足分离原理。为此,我们希望找到一个代数等价的系统,这个系统的系统矩阵是个广义上三角矩阵,且对角线上的元素正好分别是原系统在控制律作用下的系统矩阵(参考上一篇结果)和观测器的系统矩阵(A-LCm)。
我们知道,系统的状态变量是人为选择的,一个系统可以定义不同状态。同一个系统可以有很多基于状态空间描述的数学模型。但对于一个系统,不同的状态之间有着明确的数学变换关系,即非奇异线性变换关系:
存在一个可逆矩阵P,满足x1 = Px2。
因为状态需要完全表征系统动力学行为,所以不同的状态却包含相同的系统信息,自然满足线性变换的关系。反过来利用这个性质,我们可以将已知状态变换成其他状态,从而得到系统新的数学描述,即新的状态空间方程。我们称这样新旧两种系统(其实是系统描述)是代数等价的。两个代数等价系统的系统参数矩阵满足这样的变换关系:
A2 = PA1P-1 B2 = PB1 C2=C1P-1 D2 = D1 , P为适当阶的可逆矩阵。
两个代数等价的系统具有很多共有属性,除了能控、能观性之外,我们需要用到的就是代数等价系统具有相同的特征多项式和极点。为此,我们定义这样的P矩阵,对由基于估计的MPC算法得到的系统矩阵进行代数等价变形:
对原系统做相似变换:
上式中的A - BuKmpc(Sx + ICc ) 是状态全部可以测量时预测控制闭环系统的稳定性判定矩阵而A - LCm 是状态估计器的稳定性判定矩阵.因此, 基于估计的预测控制闭环系统的极点由状态全部可测时的控制器极点和状态估计器的极点组成.也就是说, 对无约束MPC 闭环系统来说, 分离原理成立, 状态反馈和估计器可以独设计.因此, 我们可以得到结论:基于估计的无约束MPC 闭环系统名义渐近稳定, 当且仅当状态反馈MPC 稳定和状态估计器稳定。