用bfs+康托展开解决3*3数字华容道问题

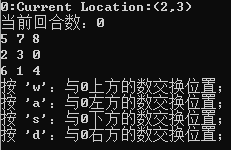
数字华容道的规则是这样的：给出一个乱序矩阵，你每次只能将数字0与其相邻的数字交换位置，通过一系列交换，将矩阵排成有序的形式（见下图，源自博主编的小游戏）。

那么，有没有一种方法，能够求出该问题的最优解（最少交换次数）呢？

我们不妨尝试下最暴力的方法：“搜索”。由于每次交换消耗的代价相等（均为1步），因此我们可以使用宽度优先搜索（bfs）。

计算状态数

要确定bfs所需的队列空间大小，首先得计算在该问题中可能出现多少种“状态”。

我们不妨将矩阵看成一个字符串，那么由排列的知识，我们可以显然地得到其总状态数为.

状态判重

如此大量的状态数，如果用普通的枚举判重，时间复杂度为，显然会超时。

所以我们应当优化状态判重的方法，由于所有状态构成了9个数字全排列的所有情况，我们可以利用康托展开给状态编号。

康托展开可以将每种状态压缩成其唯一对应的数字，从而可以通过完美哈希判重，其公式是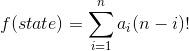：。其中为第位数字的逆序数，即位于其后的比它小的数字总数。这个公式同样可以通过一定的排列组合知识得到，本质上相当于把排列的所有情况进行了排序。

int f(int now)
{
	int p=0;
	int tot=0;
	for (int i=1;i<=9;i++)
	{
		p=0;
		for (int j=i+1;j<=9;j++)
			if (que[now][i]>que[now][j])
				p++;
		tot+=p*cantor[9-i];
	}
	return tot;
}

那么，在判重时只需要在哈希表中判断其对应的状态是否出现过即可。

交换操作

分别向上下左右交换达成新的状态，这个就比较简单了。

void move_up()
{
	if (location[head]>3) //'0'不在第一排
	{
		tail++;
		memcpy(que[tail],que[head],sizeof(que[head]));
		location[tail]=location[head];
		step[tail]=step[head]+1;
		swap(que[tail][location[tail]],que[tail][location[tail]-3]);
		location[tail]-=3;
		if (vis[f(tail)])
			tail--;
		else vis[f(tail)]=true;
	}
	return;
}
void move_down()
{
	if (location[head]<7) //'0'不在最后一排
	{
		tail++;
		memcpy(que[tail],que[head],sizeof(que[head]));
		location[tail]=location[head];
		step[tail]=step[head]+1;
		swap(que[tail][location[tail]],que[tail][location[tail]+3]);
		location[tail]+=3;
		if (vis[f(tail)])
			tail--;
		else vis[f(tail)]=true;
	}
	return;
}
void move_left()
{
	if (location[head]%3!=1) //'0'不在第一列
	{
		tail++;
		memcpy(que[tail],que[head],sizeof(que[head]));
		location[tail]=location[head];
		step[tail]=step[head]+1;
		swap(que[tail][location[tail]],que[tail][location[tail]-1]);
		location[tail]--;
		if (vis[f(tail)])
			tail--;
		else vis[f(tail)]=true;
	}
	return;
}
void move_right()
{
	if (location[head]%3!=0) //'0'不在最后一列
	{
		tail++;
		memcpy(que[tail],que[head],sizeof(que[head]));
		location[tail]=location[head];
		step[tail]=step[head]+1;
		swap(que[tail][location[tail]],que[tail][location[tail]+1]);
		location[tail]++;
		if (vis[f(tail)])
			tail--;
		else vis[f(tail)]=true;
	}
	return;
}

目标状态判断

目标状态转换成字符串后其实就是：“1234567890”，通过康托展开可以求得其对应的编码为46233，那么每次出现新状态，直接判断其是否一致即可。

另外，在宽搜中，首先达到目标状态的，一定为最优解。因此只要达到目标状态，便可直接退出程序。

bool check() //判断是否达到目标状态 
{
	if (f(tail)==46233)
		return true;
	else return false;
}

输出完整方案

我们可以用一个数组last表示队列中某个状态是由哪一个状态转移而来，那么只要从目标状态回溯一遍，即可求出完整方案。（此处代码略）

完整代码

#include
#include
#include
using namespace std;
	int head,tail;
	int cantor[10];
	int step[362881];
	int location[362881];
	char a[4][4];
	char que[362881][10];
	bool vis[362881];
int f(int now)
{
	int p=0;
	int tot=0;
	for (int i=1;i<=9;i++)
	{
		p=0;
		for (int j=i+1;j<=9;j++)
			if (que[now][i]>que[now][j])
				p++;
		tot+=p*cantor[9-i];
	}
	return tot;
}
void move_up()
{
	if (location[head]>3) //'0'不在第一排
	{
		tail++;
		memcpy(que[tail],que[head],sizeof(que[head]));
		location[tail]=location[head];
		step[tail]=step[head]+1;
		swap(que[tail][location[tail]],que[tail][location[tail]-3]);
		location[tail]-=3;
		if (vis[f(tail)])
			tail--;
		else vis[f(tail)]=true;
	}
	return;
}
void move_down()
{
	if (location[head]<7) //'0'不在最后一排
	{
		tail++;
		memcpy(que[tail],que[head],sizeof(que[head]));
		location[tail]=location[head];
		step[tail]=step[head]+1;
		swap(que[tail][location[tail]],que[tail][location[tail]+3]);
		location[tail]+=3;
		if (vis[f(tail)])
			tail--;
		else vis[f(tail)]=true;
	}
	return;
}
void move_left()
{
	if (location[head]%3!=1) //'0'不在第一列
	{
		tail++;
		memcpy(que[tail],que[head],sizeof(que[head]));
		location[tail]=location[head];
		step[tail]=step[head]+1;
		swap(que[tail][location[tail]],que[tail][location[tail]-1]);
		location[tail]--;
		if (vis[f(tail)])
			tail--;
		else vis[f(tail)]=true;
	}
	return;
}
void move_right()
{
	if (location[head]%3!=0) //'0'不在最后一列
	{
		tail++;
		memcpy(que[tail],que[head],sizeof(que[head]));
		location[tail]=location[head];
		step[tail]=step[head]+1;
		swap(que[tail][location[tail]],que[tail][location[tail]+1]);
		location[tail]++;
		if (vis[f(tail)])
			tail--;
		else vis[f(tail)]=true;
	}
	return;
}
void first()
{
	cantor[0]=1;
	for (int i=1;i<=9;i++)
		cantor[i]=cantor[i-1]*i;
	return;
}
bool check() //判断是否达到目标状态 
{
	if (f(tail)==46233)
		return true;
	else return false;
}
void print()
{
	for (int i=1;i<=3;i++)
	{
		for (int j=1;j<=3;j++)
			printf("%c ",que[head][(i-1)*3+j]);
		printf("\n");
	}
	printf("\n");
	return;
}
int main()
{
	for (int i=1;i<=3;i++)
		for (int j=1;j<=3;j++)
		{
			a[i][j]=getchar();
			while (a[i][j]<'0'||a[i][j]>'9')
				a[i][j]=getchar();
			que[1][(i-1)*3+j]=a[i][j];
			if (a[i][j]=='0')
				location[1]=(i-1)*3+j;
		}
	first();
	head=1;
	tail=1;
	vis[f(1)]=true;
	if (check())
	{
		printf("0");
		return 0; 
	}
	while (head<=tail)
	{
		//print();
		move_up();
		if (check())
		{
			printf("%d",step[tail]);
			return 0;
		}
		move_down();
		if (check())
		{
			printf("%d",step[tail]);
			return 0;
		}
		move_left();
		if (check())
		{
			printf("%d",step[tail]);
			return 0;
		}
		move_right();
		if (check())
		{
			printf("%d",step[tail]);
			return 0;
		}
		head++;
	}
	printf("No Solution");
	return 0;
}