字典树(原理+模板)
一:原理(转自:https://www.cnblogs.com/TheRoadToTheGold/p/6290732.html)
Trie树(字典树)
一、引入
字典是干啥的?查找字的。
字典树自然也是起查找作用的。查找的是啥?单词。
看以下几个题:
1、给出n个单词和m个询问,每次询问一个单词,回答这个单词是否在单词表中出现过。
答:简单!map,短小精悍。
好。下一个
2、给出n个单词和m个询问,每次询问一个前缀,回答询问是多少个单词的前缀。
答:map,把每个单词拆开。
judge:n<=200000,TLE!
这就需要一种高级数据结构——Trie树(字典树)
二、原理
在本篇文章中,假设所有单词都只由小写字母构成
对cat,cash,app,apple,aply,ok 建一颗字典树,建成之后如下图所示
![]()
由此可以看出:
1、字典树用边表示字母
2、有相同前缀的单词公用前缀节点,那我们可以的得出每个节点最多有26个子节点(在单词只包含小写字母的情况下)
3、整棵树的根节点是空的。为什么呢?便于插入和查找,这将会在后面解释。
4、每个单词结束的时候用一个特殊字符表示,图中用的‘′,那么从根节点到任意一个‘′,那么从根节点到任意一个‘’所经过的边的所有字母表示一个单词。
三、基本操作
A、insert,插入一个单词
1.思路
从图中可以直观看出,从左到右扫这个单词,如果字母在相应根节点下没有出现过,就插入这个字母;否则沿着字典树往下走,看单词的下一个字母。
这就产生一个问题:往哪儿插?计算机不会自己选择位置插,我们需要给它指定一个位置,那就需要给每个字母编号。
我们设数组trie[i][j]=k,表示编号为i的节点的第j个孩子是编号为k的节点。
什么意思呢?
这里有2种编号,一种是i,k表示节点的位置编号,这是相对整棵树而言的;另一种是j,表示节点i的第j的孩子,这是相对节点i而言的。
不理解?看图
还是单词cat,cash,app,apple,aply,ok
我们就按输入顺序对其编第一种号,红色表示编号结果。因为先输入的cat,所以c,a,t分别是1,2,3,然后输入的是cash,因为c,a是公共前缀,所以从s开始编,s是4,以此类推。
注意这里相同字母的编号可能不同
![]()
第二种编号,相对节点的编号,紫色表示编号结果。
因为每个节点最多有26个子节点,我们可以按他们的字典序从0——25编号,也就是他们的ASCLL码-a的ASCLL码。
注意这里相同字母的编号相同
![]()
实际上每个节点的子节点都应该从0编到——25,但这样会发现许多事根本用不到的。比如上图的根节点应该分出26个叉。节约空间,用到哪个分哪个。
这样编号有什么用呢?
回到数组trie[i][j]=k。 数组trie[i][j]=k,表示编号为i的节点的第j个孩子是编号为k的节点。
那么第二种编号即为j,第一种编号即为i,k
2、代码
void insert()//插入单词s
{
len=strlen(s);//单词s的长度
root=0;//根节点编号为0
for(int i=0;i
B、search,查找
查找有很多种,可以查找某一个前缀,也可以查找整个单词。
再次我们以查找一个前缀是否出现过为例讲解
1、思路
从左往右以此扫描每个字母,顺着字典树往下找,能找到这个字母,往下走,否则结束查找,即没有这个前缀;前缀扫完了,表示有这个前缀。
2、代码
bool find()
{
len=strlen(s);
root=0;//从根结点开始找
for(int i=0;s[i];i++)
{
int x=s[i]-'a';//
if(trie[root][x]==0) return false;//以root为头结点的x字母不存在,返回0
root=trie[root][x];//为查询下个字母做准备,往下走
}
return true;//找到了
}3、如果是查询某个单词的话,我们用bool变量 v[i]表示节点i是否是单词结束的标志。
那么最后return的是v[root],所以在插入操作中插入完每个单词是,要对单词最后一个字母的v[i]置为true,其他的都是false
4、如果是查询前缀出现的次数的话,那就在开一个sum[],表示位置i被访问过的次数,
那么最后return的是sum[root],插入操作中每访问一个节点,都要让他的sum++
这里前缀的次数是标记在前缀的最后一个字母所在位置的后一个位置上。
比如:前缀abc出现的次数标记在c所在位置的后一个位置上,
![]()
四、完整代码
1、查询是否出现
/*
trie tree的储存方式:将字母储存在边上,边的节点连接与它相连的字母
trie[rt][x]=tot:rt是上个节点编号,x是字母,tot是下个节点编号
*/
#include
#include
#include
#include
#define maxn 2000010
using namespace std;
int tot=1,n;
int trie[maxn][26];
//bool isw[maxn];查询整个单词用
void insert(char *s,int rt)
{
for(int i=0;s[i];i++)
{
int x=s[i]-'a';
if(trie[rt][x]==0)//现在插入的字母在之前同一节点处未出现过
{
trie[rt][x]=++tot;//字母插入一个新的位置,否则不做处理
}
rt=trie[rt][x];//为下个字母的插入做准备
}
/*isw[rt]=true;标志该单词末位字母的尾结点,在查询整个单词时用到*/
}
bool find(char *s,int rt)
{
for(int i=0;s[i];i++)
{
int x=s[i]-'a';
if(trie[rt][x]==0)return false;//以rt为头结点的x字母不存在,返回0
rt=trie[rt][x];//为查询下个字母做准备
}
return true;
//查询整个单词时,应该return isw[rt]
}
char s[22];
int main()
{
tot=0;
int rt=1;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
cin>>s;
insert(s,rt);
}
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
cin>>s;
if(find(s,rt))printf("YES\n");
else printf("NO\n");
}
return 0;
} 2、查询前缀出现次数
#include
#include
#include
#include
using namespace std;
int trie[400001][26],len,root,tot,sum[400001];
bool p;
int n,m;
char s[11];
void insert()
{
len=strlen(s);
root=0;
for(int i=0;i>s;
insert();
}
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
cin>s;
printf("%d\n",search());
}
}
指针写法:
#include
#include
#include
#include
using namespace std;
char s[11];
int n,m;
bool p;
struct node
{
int count;
node * next[26];
}*root;
node * build()
{
node * k=new(node);
k->count=0;
memset(k->next,0,sizeof(k->next));
return k;
}
void insert()
{
node * r=root;
char * word=s;
while(*word)
{
int id=*word-'a';
if(r->next[id]==NULL) r->next[id]=build();
r=r->next[id];
r->count++;
word++;
}
}
int search()
{
node * r=root;
char * word=s;
while(*word)
{
int id=*word-'a';
r=r->next[id];
if(r==NULL) return 0;
word++;
}
return r->count;
}
int main()
{
root=build();
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
cin>>s;
insert();
}
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
cin>>s;
printf("%d\n",search());
}
}
二:模板(转自:http://www.cnblogs.com/fzl194/p/8950876.html)
1:输入字符串,查询是不是单词或者前缀
查询单词的时候,在插入时在最后一个节点的地方标记为单词,查询时返回最后节点是不是单词标记
const int maxn = 1e6 + 10;
int tree[maxn][26];
//字典树tree[u][v]表示编号为u的节点的下一个字母为v连接的节点的编号
int idx(char c){ return c - 'a'; }//可以写成宏定义
int tot = 1;//根节点编号为1
bool is_word[maxn];//单词结束标记
void Insert(char s[], int u)//u表示根节点
//插入字符串s
{
for(int i = 0; s[i]; i++)
{
int c = idx(s[i]);
if(!tree[u][c])
tree[u][c] = ++tot;
u = tree[u][c];
}
//is_word [u] = true; //查询单词的时候需要标记最后一个节点的地方是单词
}
bool Find(char s[], int u)
//查询s是否是前缀
{
for(int i = 0; s[i]; i++)
{
int c = idx(s[i]);
if(!tree[u][c])
return false;
u = tree[u][c];
}
return true;
//return is_word[u]; //查询s是否是单词的时候,需要返回当前是不是单词结束标志
}2:统计前缀出现的次数:
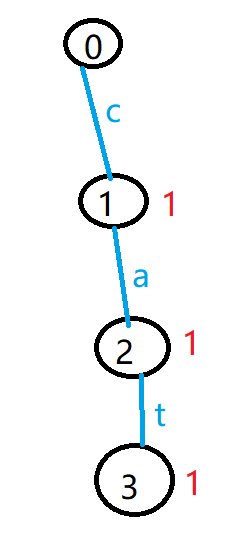
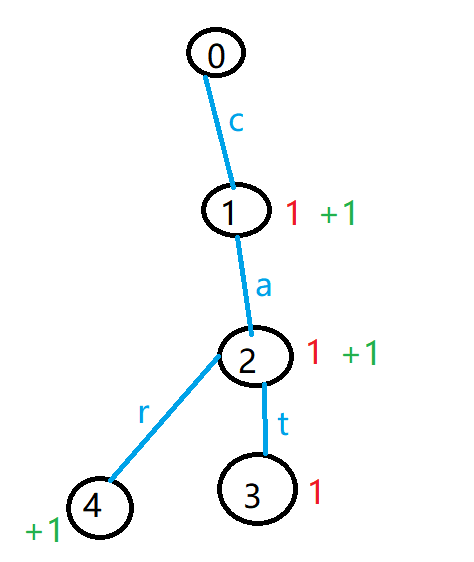
由于字典树中字母是边,节点是编号,统计前缀出现次数时,开一个sum数组表示该编号为终点的前缀出现次数,在每次加入一个字母的时候,总是在这条字母表示的边的后面那个节点加一。
比如下图,红色表示每个节点为终点的前缀出现的次数,每个字母表示边。
这里在每条边的后面那个节点上表示该前缀出现的次数。
如果在每条边的前面那个节点上表示该前缀出现的次数,会导致错误,因为根节点就不知道到底表示成什么字母出现的次数
查询c为前缀的数目的时候返回编号1的sum值
查询ca为前缀的数目的时候返回编号2的sum值
const int maxn = 1e6 + 10;
int tree[maxn][26];
//字典树tree[u][v]表示编号为u的节点的下一个字母为v连接的节点的编号
int idx(char c){ return c - 'a'; }//可以写成宏定义
int tot = 1;//根节点编号为1
int sum[maxn];//标记以该节点结束的前缀出现次数
void Insert(char s[], int u)//u表示根节点
//插入字符串s
{
for(int i = 0; s[i]; i++)
{
int c = idx(s[i]);
if(!tree[u][c])
tree[u][c] = ++tot;
sum[tree[u][c]]++; //前缀后面的那个节点数目加一
u = tree[u][c];
}
}
int Find_sum(char s[], int u)
{
for(int i = 0; s[i]; i++)
{
int c = idx(s[i]);
if(!tree[u][c])return 0;
u = tree[u][c];
}
return sum[u];//返回最后一个字母表示的边连接的后面那个节点,所记录的sum值
}3:删除包含某前缀的所有单词
void Delete(char s[], int u)//删除所有包含该前缀的单词
{
int cnt = Find_sum(s, u);
if(cnt <= 0)return;
for(int i = 0; s[i]; i++)//前缀路径上全部删去cnt个单词
{
int c = idx(s[i]);
if(!tree[u][c])return;
sum[u] -= cnt;
u = tree[u][c];
}
sum[u] = 0;//最末尾直接赋值成0
for(int i = 0; i < 26; i++)//最末尾的每个子节点全部清空
tree[u][i] = 0;
}