【原创】【Python 3.6】【人工智能】从零开始，使用CIFAR10图像识别数据库，创建含一层隐含层的浅层神经网络

CIFAR10数据库

CIFAR10是一套含有60000张大小为32×32彩色RGB图像的10分类图像数据库，其中的50000张图像为训练数据，10000张图像为测试数据，另外验证集的数据是从训练集中取出的。可以在下列网站下载CIFAR10数据库：
CIFAR10数据库下载地址

含一层隐含层的浅层神经网络

神经网络的介绍在网络上有很多，在此就不赘述，这里主要介绍本网络使用的一些超参数：
网络结构：输入层 -> 隐含层 -> 输出层
隐含层使用的激活函数：ReLU函数
输出层使用的损失函数：Softmax函数
训练集数据特征数量（即维度）：32×32×3，3表示有RGB三个色彩通道
训练集数据量：49000
验证集数据量：1000
由于该案例并不专注于识别准确率，而是专注于如何使用代码实现该网络，所以不需要测试集。
隐含层神经元数量：100
初始权重矩阵的标准差：0.001
训练迭代次数：2000
每个批次的训练集数量：500
输出层神经元数量：10，即输出10个类别
学习率：0.001
正则化系数：0.6
学习率衰减率：0.95

训练结果

损失函数曲线中的噪声是由随机批量梯度下降引起的。
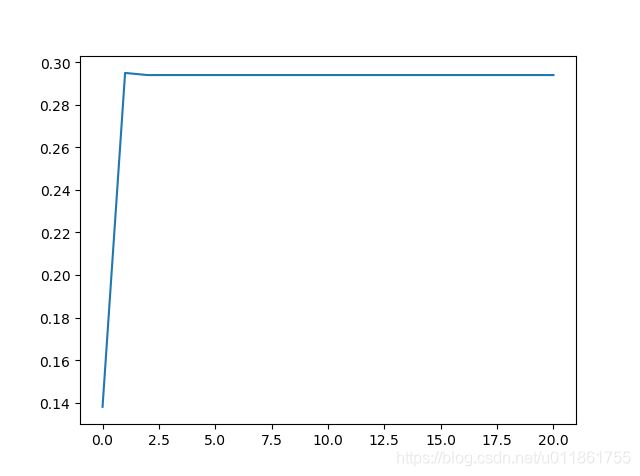
训练准确率的高低起伏是由每个批次的训练集是随机在49000张训练集数据中选取而引起的。
历次训练的损失值：

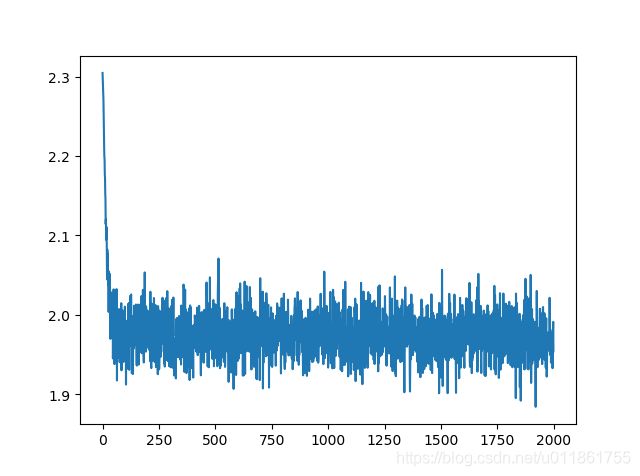
训练准确率曲线：

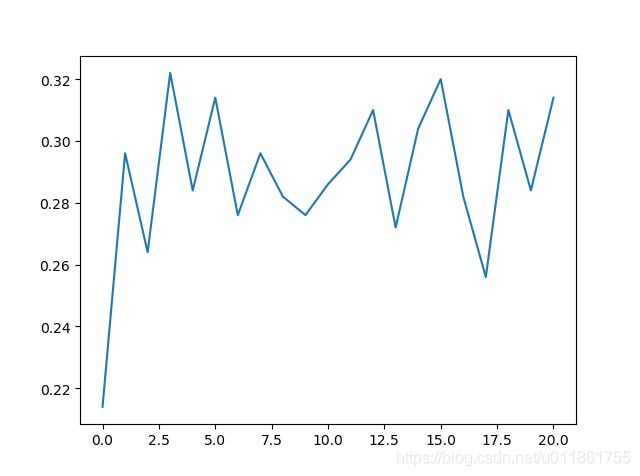
验证准确率曲线：

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import os
import _pickle as pickle

#获取CIFAR10图像数据集
def get_CIFAR10_data(num_training=49000, num_validation=1000, num_test=0):
    cifar10_dir = 在这里写明CIFAR10图像数据库的文件夹路径，例如'E:/cifar-10-batches-py'
    xs = []
    ys = []
    for b in range(1,6):
        f = os.path.join(cifar10_dir, 'data_batch_%d' % (b, ))
        with open(f, 'rb') as f:
            datadict = pickle.load(f, encoding = 'latin1')
            X = datadict['data']
            Y = datadict['labels']
            X = X.reshape(10000, 3, 32, 32).transpose(0,2,3,1).astype("float")
            Y = np.array(Y)
        xs.append(X)
        ys.append(Y)    
    X_train = np.concatenate(xs)
    y_train = np.concatenate(ys)
    del X, Y
    with open(os.path.join(cifar10_dir, 'test_batch'), 'rb') as f:
        datadict = pickle.load(f, encoding = 'latin1')
        X_test = datadict['data']
        y_test = datadict['labels']
        X_test = X_test.reshape(10000, 3, 32, 32).transpose(0,2,3,1).astype("float")
        y_test = np.array(y_test)
    #从原始训练集的50000张图中选出最后1000张图作为验证集
    mask = range(num_training, num_training + num_validation)
    X_val = X_train[mask]
    y_val = y_train[mask]
    mask = range(num_training)
    X_train = X_train[mask]
    y_train = y_train[mask]
    #从原始测试集中的10000张图中选出最开始的1000张图作为测试集
    mask = range(num_test)
    X_test = X_test[mask]
    y_test = y_test[mask]
    #将训练集数据进行中心化
    mean_image = np.mean(X_train, axis=0)
    X_train -= mean_image
    X_val -= mean_image
    X_test -= mean_image
    #重构尺寸
    X_train = X_train.transpose(0, 3, 1, 2).copy()
    X_val = X_val.transpose(0, 3, 1, 2).copy()
    X_test = X_test.transpose(0, 3, 1, 2).copy()
    return {
      'X_train': X_train, 'y_train': y_train,
      'X_val': X_val, 'y_val': y_val,
      'X_test': X_test, 'y_test': y_test,
    }

#前向传播
def affine_forward(x, w, b):
    """
    计算某一层的前向传播。
    输入：x，N*D，若为RGB图像，则为N*(长*宽*3)，N为本层的神经元数量，D为特征数量
          w，D*M，M为下一层的神经元数量
          b，偏置向量，M*1
    返回：out，N*M
    """
    out = None
    #数据量
    N = x.shape[0]
    #将x整理成二维数组，N行，剩下的组成列
    x = np.reshape(x, (N,-1))
    #在数据矩阵的最后一列再添加一列1，作为偏置x0，x变成N*(D+1)
    x = np.hstack((x, np.ones((N, 1))))
    #将偏置向量b添加到权重矩阵w的最后一行，作为偏置x0的权重，w变成(D+1)*M
    w = np.vstack((w, np.transpose(b)))
    #计算下一层所有神经元对本层所有神经元的激活值，例如本层有2个神经元，下一层有3个，则输出2*3矩阵
    out = x.dot(w)
    return out

#反向传播
def affine_backward(dout, cache):
    """
    计算反向传播
    输入：
    dout，上层梯度，即残差，N*M
    输出：
    dx，输入数据的梯度，N*d1*d2*...*dk
    dw，权重矩阵的梯度，D*M
    db，偏置项b的梯度，M*1
    """
    x, w, b = cache
    dx, dw, db = None, None, None
    #反向传播
    #数据量
    N = x.shape[0]
    #将x重塑成N*D
    x = np.reshape(x, (N, -1))
    #计算残差的梯度
    dx = dout.dot(np.transpose(w))
    #计算权重的梯度
    dw = np.transpose(x)
    dw = dw.dot(dout)
    #计算偏置的梯度
    db = np.sum(dout, axis = 0)
    #将dx重塑回来
    dx = np.reshape(dx, x.shape)
    return dx, dw, db

#RelU传播
def relu_forward(x):
    """
    计算ReLUs激活函数的前向传播，然后保存结果。
    输入：
    x - 输入数据
    返回：
    out - 与输入数据的尺寸相同。
    """
    out = None
    out = np.max(np.dstack((x,np.zeros(x.shape))),axis = 2)
    return out

#ReLU反向传播
def relu_backward(dout, x):
    """
    计算ReLU函数的反向传播。
    输入：
    dout - 上层误差梯度
    x - 输入数据x
    返回：
    dx - x的梯度
    """
    dx = dout
    dx[x <= 0] = 0
    return dx

#softmax损失函数
def softmax_loss(X, y):
    """
    无正则化
    输入：
    X：神经网络的输出层激活值
    y：训练数据的标签，即真实标签
    reg：正则化惩罚系数
    输出：
    loss：损失值
    dx：梯度
    """
    #初始化损失值与梯度
    loss = 0.0
    #计算损失-------------
    #训练集数据数量N
    num_train = X.shape[0]
    #数据类别数量C
    num_catogries = X.shape[1]
    #归一化概率的分子，N*C
    #为了防止指数运算时结果太大导致溢出，这里要将X的每行减去每行的最大值
    score_fenzi = X - np.max(X, axis = 1, keepdims = True)
    score_fenzi = np.exp(score_fenzi)
    #归一化概率的分母，即，将归一化概率的分子按行求和，N*1
    score_fenmu = np.sum(score_fenzi, axis = 1, keepdims = True)
    #将分母按列复制，
    score_fenmu = score_fenmu.dot(np.ones((1, num_catogries)))
    #归一化概率，N*C/(N*1)*(1*C)=N*C/N*C
    prob = np.log(score_fenzi/score_fenmu)
    y_true = np.zeros((num_train,  num_catogries))
    #把训练数据的标签铺开，例如，x是第3类，则x对应的标签为[0,0,1,0,0,0,0,0,0,0]
    y_true[range(num_train), y] = 1.0
    #y_true与p对应元素相乘后，只留下了每个数据真实标签对应的分数，例如x属于第3类，则留下第3个归一化概率
    #求出每一行归一化概率的和，即把多余的0消除，再计算所有数据归一化概率的和
    loss = -np.sum(y_true * prob) / num_train
    #计算梯度--------------
    dx = (score_fenzi/score_fenmu).copy()
    dx[np.arange(num_train), y] -= 1
    dx /= num_train
    return loss, dx

#导入CIFAR10数据库
data = get_CIFAR10_data()
X_train = data['X_train']
y_train = data['y_train']
X_val = data['X_val']
y_val = data['y_val']
X_test = data['X_test']
y_test = data['y_test']
for k, v in data.items():
    print(f"{k}：", v.shape)

#测试含一层隐含层的神经网络-------------------------------------------------

#网络超参数设置
weight_scale = 1e-3 #初始权重矩阵中各元素的标准差
input_dim = 32*32*3 #输入数据的特征数量，即维度
hidden_dim = 100 #隐含层神经元数量
num_classes = 10 #输出层神经元数量
params = {} #初始化存储有权重矩阵和偏置矩阵的字典
print("参数初始化...",  end = '')
#初始化输出层到隐含层的权重W1与偏置b1与隐含层到输出层的权重W2与偏置b2
params['W1'] = weight_scale * np.random.randn(input_dim, hidden_dim)
params['b1'] = np.zeros(hidden_dim)
params['W2'] = weight_scale * np.random.randn(hidden_dim, num_classes)
params['b2'] = np.zeros(num_classes)
print('完成')

#输入数据
print('输入数据...', end = '')
X = X_train #训练集数据
y = y_train #训练集标签
print('完成')

#开始训练
#输入训练超参数
num_iters = 2000 #迭代次数
batch_size = 500 #每一次迭代中从训练集中随机选取的数据量，选取出来作为一个批次
learning_rate = 1e-3 #学习率
verbose = True #是否在命令行显示训练消息
reg = 0.0 #正则化系数
learning_rate_decay = 0.95 #学习率衰减率
iterations_per_epoch = X_train.shape[0] / batch_size #遍历整个训练集需要多少个批次
#存储历次迭代的损失值、训练准确率与验证准确率
loss_history = [] #历次损失值
train_history = [] #历次训练准确率
val_history = [] #历次验证准确率
#存储每次迭代生成的权重梯度与偏置梯度的字典
grad = {}
for it in range(num_iters):
    num_train = X.shape[0] #训练集中的总数据量
    X_batch = None
    y_batch = None
    #从训练集中随机取出batch_size个训练数据
    #从0到num_train-1中随机取batch_size个数字，作为一个批次的训练数据的索引
    i = np.random.choice(range(num_train), batch_size, replace = False)
    X_batch = X[i,:]
    #标签y和训练数据X必须对应，例如取出了第3个数据，则必须取出第3个标签
    y_batch = y[i]
    #前向传播------------------------
    #从输入层传到隐含层，注意只有隐含层才有激活函数
    forward_out_1 = affine_forward(X_batch, params['W1'], params['b1'])
    forward_relu_out = relu_forward(forward_out_1)
    #从隐含层到输出层
    scores = affine_forward(forward_relu_out, params['W2'], params['b2'])
    #在输出层使用softmax损失函数，计算网络的总损失与梯度
    loss, grad_out = softmax_loss(scores, y_batch)
    #对总损失加入正则项
    loss += 0.5 * reg * (np.sum(params['W1'] ** 2) + np.sum(params['W2'] ** 2))
    #存储损失值
    loss_history.append(loss)
    #反向传播-------------------------------------------------------------------
    #计算输出层到隐含层的残差、权重梯度与偏置梯度
    dx2, grad['W2'], grad['b2'] = affine_backward(grad_out, (forward_relu_out, params['W2'], params['b2']))
    #对输出层到隐含层的权重梯度加入正则项
    grad['W2'] += reg * params['W2']
    #计算隐含层到输入层的残差、权重梯度与偏重梯度
    relu_dx1 = relu_backward(dx2, forward_relu_out)
    dx1, grad['W1'], grad['b1'] = affine_backward(relu_dx1, (X_batch, params['W1'], params['b1']))
    #对第一层隐含层的权重梯度加入正则项
    grad['W1'] += reg * params['W1']
    #反向传播完成，此时回到了输入层
    #通过梯度和学习率更新权重与偏置
    params['W1'] -= learning_rate * grad['W1']
    params['W2'] -= learning_rate * grad['W2']
    params['b1'] -= learning_rate * grad['b1']
    params['b2'] -= learning_rate * grad['b2']
    if verbose and it % batch_size == 0:
        print(f"第{it}/{num_iters}次迭代，损失为{loss}，", end = '')
    if it % iterations_per_epoch == 0:
        #做一个预测，计算此次迭代的训练准确率、验证准确率
        pred_out_1 = affine_forward(X_batch, params['W1'], params['b1'])
        pred_relu_out = relu_forward(pred_out_1)
        pred_out_2 = affine_forward(pred_relu_out, params['W2'], params['b2'])
        pred_out = np.argmax(pred_out_2, axis = 1)
        valpred_out_1 = affine_forward(X_val, params['W1'], params['b1'])
        valpred_relu_out = relu_forward(valpred_out_1)
        valpred_out_2 = affine_forward(valpred_relu_out, params['W2'], params['b2'])
        valpred_out = np.argmax(valpred_out_2, axis = 1)
        #计算训练准确率、验证准确率
        train_acc = np.mean(pred_out == y_batch)
        train_history.append(train_acc)
        val_acc = np.mean(valpred_out == y_val)
        val_history.append(val_acc)
        print(f'训练准确度为{train_acc}, 验证准确度为{val_acc}')
    #学习率衰减
    learning_rate *= learning_rate_decay
    
#结果显示
plt.figure(1)
plt.plot(loss_history)
plt.title('Training Loss')
plt.figure(2)
plt.plot(train_history)
plt.title('Training Accuracy')
plt.figure(3)
plt.plot(val_history)
plt.title('Validation Accuracy')