数据结构~13.遍历二叉树的四个应用案例
数据结构学习~13.遍历二叉树的四个应用案例
本文是上一篇文章的后续,详情点击该链接~
案例1
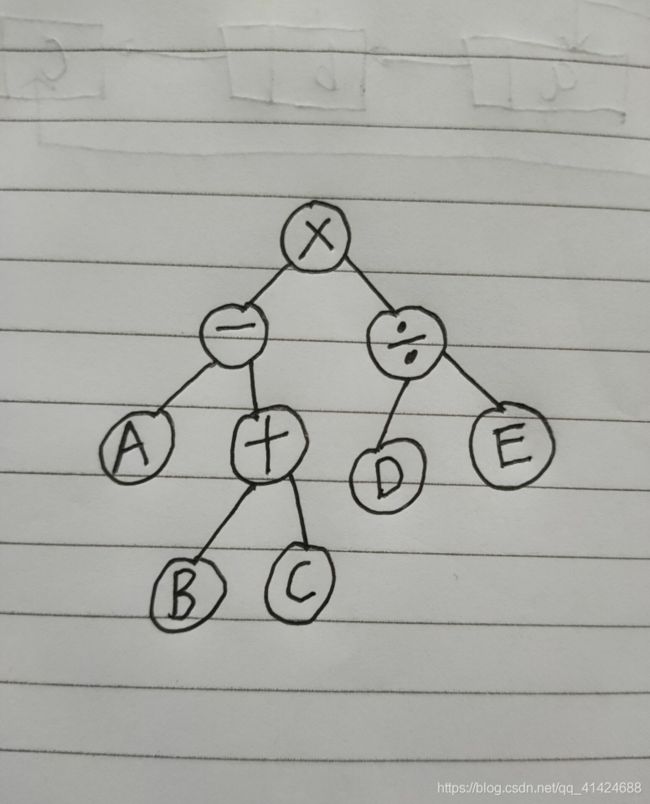
表达式(a-(b+c))*(d/e)存储在图下的一颗二叉树当中(二叉树的data域中是字符型)。编写程序求出该表达式。
做此题之前,可以在我上一篇文章里面,把素材复制过来。
代码实现
我们先写一个运算函数,方便下面使用(该代码曾出现在 09.顺序栈和链栈的应用~ 中)
int operation(int a, char op, int b) {
if (op == '+') return a + b;
if (op == '-') return a - b;
if (op == '*') return a * b;
if (op == '/') {
//被除数不能为0!
if (b == 0) {
printf("error");
return 0;
}
else {
return a / b;
}
}
}
遍历实现
int comp(Tree *p) {
int A, B;
if (p != NULL) {
//如果说这个结点,它的左子树和右子树都不是空。那么就用后序遍历求值
if (p ->left != NULL && p->right != NULL) {
//后序遍历求出左子树的值,赋值给A
A = comp(p->left);
//后序遍历求出右子树的值,赋值给B
B = comp(p->right);
//返回运算结果
return operation(A, p->data,B);
}
else {
//如果当前左右子树为空,则为数值,直接返回
return p->data - '0';
}
}
else {
//如果是空树,直接返回-1
return -1;
}
}
构建图中的二叉树,进行测试。设A = 3,B=4,C=5,D=6,E=2
int main(int argc, char* argv[]) {
//根据图中的样式构建一颗二叉树
//设A = 3,B=4,C=5,D=6,E=2
char A = '3', B = '4', C = '5', D = '6', E = '2';
Tree* tree = (Tree*)malloc(sizeof(Tree));
tree = getTree('*');
tree->left = getTree('-');
tree->left->left = getTree(A);
tree->left->right = getTree('+');
tree->left->right->left = getTree(B);
tree->left->right->right = getTree(C);
tree->right = getTree('/');
tree->right->left = getTree(D);
tree->right->right = getTree(E);
//开始运算
int n = comp(tree);
//测试是否成功
printf("(3-(4+5))*(6/2) = %d\n", (3 - (4 + 5)) * (6 / 2));
printf("二叉树的遍历运算为: %d",n);
getchar();
return 0;
}
测试结果是正确的
案例2
写一个算法求一颗二叉树的深度
如果有一棵二叉树,左子树的深度为L,右子树的深度为R。那么整棵树的深度就是max(L,R)+1。也就是左子树和右子树的深度中,谁最大,就让谁+1。所以说,我们只需要先求出左子树的深度,再求出右子树的深度,再套上那个公式就行了~
int getTreeDepth(Tree *p) {
//分别标识左右子树的深度
int L, R;
if (p == NULL) {
//如果是空树,那就肯定是0了
return 0;
}
else {
//求左子树的深度
L = getTreeDepth(p->left);
R = getTreeDepth(p->right);
//用最大的那个+1,便是了
return (L > R ? L : R) + 1;
}
}
案例3
在一棵以二叉链表为存储的二叉树中,查找data域值等于key值的结点是否存在(找到任何一个满足要求的结点即可),如果存在就用p指向这个结点,否则p就是null。
因为题中二叉树各个结点data域的值没有任何规律,所以要判断是否存在data域值等于key的结点就必须把所有结点都访问一遍,挨个判断是不是等于key。所以这里又会用到二叉树的遍历方式来解决
//假设二叉树已存在并且tree指向其根结点
//这里p定义要是引用型指针,因为是需要改变的
void search(Tree *tree,Tree *&p,char key) {
//如果说这棵树是空树,那就什么都不做吧!
if (tree != NULL) {
//如果tree指的结点data域值等于key,那就将p指向域值等于key的结点
if (tree->data == key) {
p = tree;
}
else {
//在左子树查找
search(tree->left,p,key);
//在右子树查找
search(tree->right,p,key);
}
}
}
案例4
编写一个程序,输出先序遍历序列中第k个结点的值。k不能大于总结点树
void findTreeNode(Tree *tree,int k) {
if (tree != NULL) {
++n;
if (k == n) {
//如果是,则输出
printf("第 %d 个结点是 %c ",k,tree->data);
//退出程序
return;
}
findTreeNode(tree->left,k);
findTreeNode(tree->right, k);
}
}
假如说改成中序或者后续,那还是一样的套路
//中序
void findTreeNodeMid(Tree* tree, int k) {
if (tree != NULL) {
findTreeNodeMid(tree->left, k);
++n;
if (k == n) {
//如果是,则输出
printf("第 %d 个结点是 %c ", k, tree->data);
//退出程序
return;
}
findTreeNodeMid(tree->right, k);
}
}
//后序
void findTreeNodeLast(Tree* tree, int k) {
if (tree != NULL) {
findTreeNodeLast(tree->left, k);
findTreeNodeLast(tree->right, k);
++n;
if (k == n) {
//如果是,则输出
printf("第 %d 个结点是 %c ", k, tree->data);
//退出程序
return;
}
}
}
完整代码
#include