线性判别分析LDA算法与python实现
降维指的是通过某种数学变换将高维原始空间的属性转变为低维子空间,根据变换形式可将该数学变换分为线性变换和非线性变换,对应的降维算法也被称为线性降维和非线性降维.其中,线性降维算法主要有线性判别分析(linear discriminant analysis,LDA)和主成分分析(Principal Component Analysis,PCA),非线性降维主要有核化思想(如Kernelized PCA)和流形学习(Isomap,LLE,LE等)两类.
假定有原始空间高维数据 X ∈ R n × m X \in R^{n \times m} X∈Rn×m,其中 n n n为样本数, m m m为样本长度,现我们要求 X X X的低维嵌入 Y ∈ R n × d Y \in R^{n \times d} Y∈Rn×d,其中 d < < m d<

首先盗用西瓜书里的一张图,这张图很清晰地阐释了LDA的核心思想:图中的数据简化为二维降维到一维,降维过程中,LDA算法使得低维空间中,同一类的数据尽可能接近,使得不同类数据尽可能远离.如上文所述,LDA是一种监督学习算法,即数据具有label,这里与西瓜书保持一致,使用了二分类问题的数据,分别记为 X 0 ∈ R n 0 × m X_0 \in R^{n_0 \times m} X0∈Rn0×m与 X 1 ∈ R n 1 × m X_1 \in R^{n_1 \times m} X1∈Rn1×m.我们的目标是找到一个变换矩阵 W ∈ R m × d W \in R^{m \times d} W∈Rm×d对原始数据 X X X进行线性变换 Y = X W Y=XW Y=XW,且变换后的 Y Y Y满足上述性质.记 μ 0 ∈ R m × 1 , μ 1 ∈ R m × 1 , Σ 0 ∈ R m × m , Σ 1 ∈ R m × m \mu_0 \in R^{m \times 1},\mu_1 \in R^{m \times 1},\Sigma_0 \in R^{m \times m},\Sigma_1 \in R^{m \times m} μ0∈Rm×1,μ1∈Rm×1,Σ0∈Rm×m,Σ1∈Rm×m分别为 X 0 X_0 X0的均值, X 1 X_1 X1的均值, X 0 X_0 X0的协方差, X 1 X_1 X1的协方差,则: μ i = 1 n i ∑ x ∈ X i x \mu_i=\frac{1}{n_i} \sum_{x \in X_i} x μi=ni1x∈Xi∑x Σ i = ∑ x ∈ X i ( x − μ i ) ( x − μ i ) T \Sigma_i=\sum_{x \in X_i}(x-\mu_i)(x-\mu_i)^T Σi=x∈Xi∑(x−μi)(x−μi)T 首先我们希望变换后的类间距离越大越好,我们定义类间距离为类中心的 l 2 l_2 l2距离,所以该步骤我们的目标是: m a x W ∣ ∣ W T μ 0 − W T μ 1 ∣ ∣ 2 2 {\rm max}_W \ ||W^T\mu_0-W^T\mu_1||_2^2 maxW ∣∣WTμ0−WTμ1∣∣22 即: m a x W W T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T W {\rm max}_W \ W^T(\mu_0-\mu_1)(\mu_0-\mu_1)^T W maxW WT(μ0−μ1)(μ0−μ1)TW 其次我们希望变换后的类内协方差越小越好,即: m i n W W T ( Σ 0 + Σ 1 ) W {\rm min}_W W_T (\Sigma_0+\Sigma_1) W minWWT(Σ0+Σ1)W 现定义两个矩阵,类内散度矩阵(intra-class scatter matrix) S a ∈ R m × m S_a \in R^{m \times m} Sa∈Rm×m与类间散度矩阵(inter-class scatter matrix) S r ∈ R m × m S_r \in R^{m \times m} Sr∈Rm×m: S a = Σ 0 + Σ 1 S_a=\Sigma_0+\Sigma_1 Sa=Σ0+Σ1 S r = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T S_r=(\mu_0-\mu_1)(\mu_0-\mu_1)^T Sr=(μ0−μ1)(μ0−μ1)T 我们约束 W T S a W = 1 W^T S_a W=1 WTSaW=1,所以最后的优化问题可以写成: m i n W − W T S r W {\rm min}_W \ -W^T S_r W minW −WTSrW s t . W T S a W = 1 st. \ \ W^T S_a W=1 st. WTSaW=1 定义拉格朗日函数为: L ( W ) = − W T S r W + λ ( W T S a W − 1 ) L(W)=-W^T S_r W + \lambda (W^T S_a W-1) L(W)=−WTSrW+λ(WTSaW−1) 对上述方程求 W W W的偏导,得到: S r W = λ S a W S_rW=\lambda S_aW SrW=λSaW 由上式可知, W ∈ R m × d W \in R^{m \times d} W∈Rm×d的闭解为矩阵 S a − 1 S r S_a^{-1}S_r Sa−1Sr最大的 d d d个特征值对应的 m m m维特征向量.这里公布一下代码和实验结果,代码略简略,只考虑了三维降到二维.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_classification
from mpl_toolkits.mplot3d import Axes3D
np.random.seed(0)
def createDataSet(n=100):
X0 = np.array(np.random.random((n, 3)) + 1)
X1 = np.array(np.random.random((n, 3)) - 1)
return X0, X1
def compute_W(X0, X1):
mean0 = np.mean(X0, axis=0)
mean1 = np.mean(X1, axis=0)
diff = np.expand_dims(mean0 - mean1, axis = 1)
Sr = np.matmul(diff, diff.T)
cov0 = np.matmul((X0 - mean0).T, (X0 - mean0))
cov1 = np.matmul((X1 - mean1).T, (X1 - mean1))
Sa = cov0 + cov1
# print(Sa)
tmp = np.matmul(np.linalg.pinv(Sa), Sr)
# tmp = np.matmul(np.linalg.pinv(-Sr), Sa)
eig_val, eig_vector = np.linalg.eig(tmp)
return eig_vector[:, [0,1]]
def LDA(X0, X1):
W = compute_W(X0, X1)
return np.matmul(X0, W), np.matmul(X1, W)
if __name__ == '__main__':
X0, X1 = createDataSet()
Y0, Y1 = LDA(X0, X1)
fig = plt.figure()
ax = fig.add_subplot(121, projection='3d')
ax.scatter(X0[:, 0], X0[:, 1], X0[:, 2], c=[1,0,0], cmap=plt.cm.hot)
ax.scatter(X1[:, 0], X1[:, 1], X1[:, 2], c=[0,0,1], cmap=plt.cm.hot)
ax2 = fig.add_subplot(122)
ax2.scatter(Y0[:, 0], Y0[:, 1], c=[1,0,0], cmap=plt.cm.hot)
ax2.scatter(Y1[:, 0], Y1[:, 1], c=[0,0,1], cmap=plt.cm.hot)
plt.show()
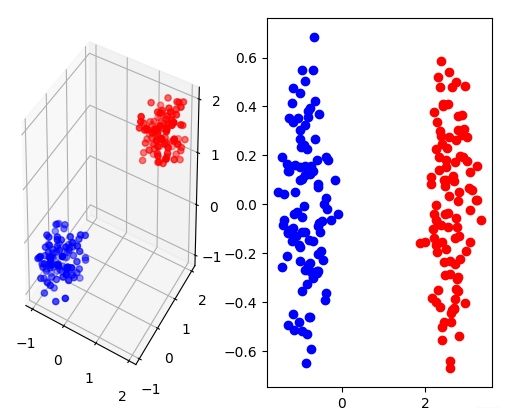
在LDA中,我们约束 W T S a W = 1 W^T S_a W=1 WTSaW=1,可能是提出算法的学者觉得类内相似对比类间差异不那么重要吧,现在我们探索一下另一种情况,我们约束 W T S r W = 1 W^T S_r W=1 WTSrW=1,那么优化问题变成了: m i n W W T S a W {\rm min}_W \ W^T S_a W minW WTSaW s t . W T S r W = 1 st. \ \ W^T S_r W=1 st. WTSrW=1 定义拉格朗日函数为: L ( W ) = W T S a W + λ ( W T S r W − 1 ) L(W)=W^T S_a W + \lambda (W^T S_r W-1) L(W)=WTSaW+λ(WTSrW−1) 对上述方程求 W W W的偏导,得到: − S a W = λ S r W -S_aW=\lambda S_rW −SaW=λSrW 由上式可知, W ∈ R m × d W \in R^{m \times d} W∈Rm×d的闭解为矩阵 − S r − 1 S a -S_r^{-1}S_a −Sr−1Sa最大的 d d d个特征值对应的 m m m维特征向量.代码中只需将21行注释,并恢复22行即可,下图展示了用这种约束得到的实验结果,可以看出两种约束并没有什么很大的差异,当然可能在高阶上第一种方法表现更优异,这里就不往下探索了.
