最短路径之迪杰斯特拉算法(Dijkstra)——贪心算法
| 迪杰斯特拉(Dijkstra)算法主要是针对没有负值的有向图,求解其中的单一起点到其他顶点的最短路径算法。本文主要总结迪杰斯特拉(Dijkstra)算法的原理和算法流程,最后通过程序实现在一个带权值的有向图中,选定某一个起点,求解到达其它节点的最短路径。 |
举个反例:

当我们使用迪杰斯特拉算法的时候,第一次更新路径长度为1的时候会确定 V 1 − − > V 2 V_{1}-->V_{2} V1−−>V2的最短路径,但是显然这不是最短的。
1.算法原理
迪杰斯特拉(Dijkstra)算法是一个按照路径长度递增的次序产生最短路径的算法。主要特点是以起始点为中心按照长度递增往外层层扩展(广度优先搜索的思想),直到扩展到终点为止。
选择最短路径顶点的时候依照的是实现定义好的贪心准则,所以该算法也是贪心算法的一种。
首先,我们引进一个辅助数组Distance,它的每个分量D[i]表示当前所找到的从起始点v0到每个终点vi的最短路径长度。
- 它的初态为:若 v 0 v_{0} v0到 v i v_{i} vi有弧,则 D [ i ] D[i] D[i]为弧上的权值;
否则,置 D [ i ] D[i] D[i]为 ∞ ∞ ∞。
显然,此时长度为
D [ j ] = M i n { D [ i ] ∣ v i ∈ V } D[j]=Min\{D[i]|v_{i}∈V\} D[j]=Min{D[i]∣vi∈V}
的路径就是从 v 0 v_{0} v0出发长度最短(为1)的一条路径,此时路径为 ( v 0 , v i ) (v_{0},v_{i}) (v0,vi)。 - 那么下一条长度次短的最短路径是哪一条?
假设该次短路径的终点是 v k v_{k} vk,则这条路径要么是 ( v 0 , v k ) (v_{0},v_{k}) (v0,vk),要么是 ( v 0 , v j , v k ) (v_{0},v_{j},v_{k}) (v0,vj,vk),即两者最短的那一条。
其中, v j ∈ S v_{j}∈S vj∈S,S为当前已求得最短路径的终点的集合;V为待求解的最短路径的顶点集合。
问题一:
为什么下一条次短路径要这样选择?(贪心准则的正确性)
不失一般性,假设S为已经求得最短路径的顶点集合,下一条最短路径的终点是 x x x,利用反证法,若此路径有一条顶点不在 S S S中,则说明存在一条终点不在S而长度比此路径长度短的路径,但是这显然是矛盾的,因为我们是按照路径长度递增的次序来产生最短路径的。
所以,下一条长度次短的路径长度应该是:
D [ j ] = M i n { D [ i ] ∣ v i ∈ V − S } D[j] = Min\{D[i] | v_{i}∈V-S\} D[j]=Min{D[i]∣vi∈V−S}
其中, D i D_{i} Di或者是弧 ( v 0 , v i ) (v_{0},v_{i}) (v0,vi)上的权值,或者是 D [ k ] ( v k ∈ S ) D[k](v_{k}∈S) D[k](vk∈S)和弧 ( v k , v i ) (v_{k},v_{i}) (vk,vi)上的权值之和。
问题二:
这样产生的路径是否就是S中对应顶点的最短路径?
- 假设以当前长度来看,假设当前长度对应的顶点v,若长度再增加,是不可能产生权值更短的路径的(对于v来说),因为长度增加的路径肯定包含此时长度的子路径,而此时选择的路径是该长度下最短的路径;
- 以一个顶点来看,源点 v 0 v_{0} v0到一顶点 v k v_{k} vk的最短路径的子路径 v 0 v_{0} v0到 v i v_{i} vi肯定也是该长度对应的最短路径(即 v 0 v_{0} v0到 v i v_{i} vi的最短路径),所以这也是我们为什么在S中选择中转结点的原因。
- 其中很大一部分原因是最短路径的最优子结构,即全局的最优解( v 0 到 v k v_{0}到v_{k} v0到vk)包含局部的最优解( v 0 v_{0} v0到v_{i}),且全局的最优解能够通过局部最优解逐步构造。
这也是迪杰斯特拉算法的贪心策略能取得最优解的原因。
2.算法流程
根据上面的算法思想,我们有下面算法的实现流程:
假设用带权值的邻接矩阵arcs来表示带权的有向图,arcs[i][j]表示弧 < v i , v j > <v_{i},v_{j}> <vi,vj>上的权值。若 < v i , v j > <v_{i},v_{j}> <vi,vj>不存在,则置arcs[i][j]为 ∞ ∞ ∞(计算机上允许的最大值)
- 1)初始化:已求顶点集S,初始状态为空集;从 v 0 v_{0} v0出发到图上其余各顶点(终点) v i v_{i} vi可能到达的最短路径长度初值:
D i s t a n c e [ i ] = a r c s [ l o c a t e ( G , v 0 ) ] [ i ] v i ∈ V Distance[i] = arcs[locate(G,v_{0})][i] \ v_{i}∈V Distance[i]=arcs[locate(G,v0)][i] vi∈V - 2)选择结点 v j v_{j} vj,使得
D i s t a n c e [ j ] = M i n { D i s t a n c e [ i ] ∣ v i ∈ V − S } Distance[j] = Min\{Distance[i] \ | \ v_{i}∈V -S \} Distance[j]=Min{Distance[i] ∣ vi∈V−S}
v j v_{j} vj就是当前求的从 v 0 v_{0} v0出发的最短路径的终点。令
S = S ∪ j S = S \cup {j} S=S∪j - 3)修改从 v 0 v_{0} v0出发到集合 V − S V-S V−S上的任一顶点 v k v_{k} vk
可达的最短路径长度。
若 D i t a n c e [ j ] + a r c s [ j ] [ k ] < D i s t a n c e [ k ] Ditance[j] + arcs[j][k] < Distance[k] Ditance[j]+arcs[j][k]<Distance[k]
则修改 D i s t a n c e [ k ] = D i t a n c e [ j ] + a r c s [ j ] [ k ] Distance[k] = Ditance[j] + arcs[j][k] Distance[k]=Ditance[j]+arcs[j][k] - 4)重复(2)(3)共 n − 1 n-1 n−1次,求的 v 0 v_{0} v0到其余个顶点的最短路径是依路径长度递增的序列。
其中,最短路径的存储可以采用一个path数组,存储到某结点的最短路径中该结点的前驱结点在图中的位置(起点 v 0 v_{0} v0的前驱可以设成 − 1 -1 −1)。
即若有下面这样一个带全有向图: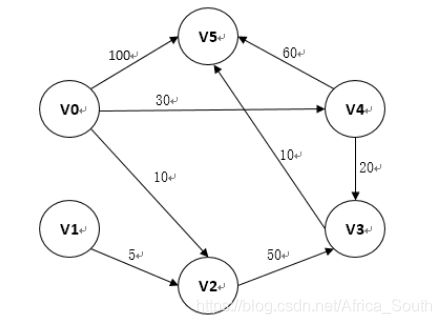
其邻接矩阵如下:
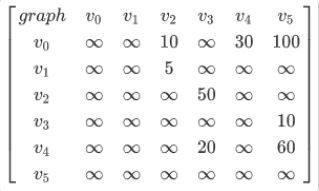
则迪杰斯特拉算法求解过程:

3.算法实现
迪杰斯特拉算法:
void ShortestPath_DIJ(MGraph G, int v0, int* path, int* distance) {
/*用Dijkstra算法求v0到其余顶点的最短路径p[n]和带权长度distance[n]
* final[i]=1表示已求得v0到vi的最短路径
*/
int* final = new int[G.vexnum];
int i;
// 初始化结点
for (i = 0; i < G.vexnum; i++) {
path[i] = -1;
final[i] = 0;
distance[i] = INT_MAX;
}
distance[v0] = 0; // 初始化源点
for (i = 0; i < G.vexnum; i++) { // 寻找不同长度的最短路径
int min = INT_MAX; // 当前所知里v0顶点的最短距离
int index = -1; // 最短距离对应的下标
int j;
for (j = 0; j < G.vexnum; j++) {
if (!final[j]) { // j在V-S中
if (distance[j] < min) {
min = distance[j];
index = j;
}
}
}// 寻找最短路径
if (index == -1) break;
final[index] = 1; // 离v0最近的顶点Index并入S,第一次一定是v0
for (j = 0; j < G.vexnum; j++) { // 更新距离矩阵,一定要判断是否达,即arcs[][]!=OO,否则会整数溢出
if (!final[j] && G.arcs[index][j] != INT_MAX && (min + G.arcs[index][j] < distance[j])) {
distance[j] = min + G.arcs[index][j];
path[j] = index;
}
}
}
delete[] final;
}
完整测试用例
#include 这里我用的是栈倒序输出,当然也有其它存储最短路径的方法。
测试用例(即上面的有向网):
6 8
V0 V1 V2 V3 V4 V5
V0 V5 100
V0 V4 30
V0 V2 10
V1 V2 5
V2 V3 50
V3 V5 10
V4 V5 60
V4 V3 20
4.时间复杂度
两个FOR循环嵌套,最后的时间复杂度为 O ( n 2 ) O(n^{2}) O(n2)。
若想要求源点到某一顶点的最短路径,也可以用Dijkstra算法,复杂度一样;
但是若要求每一对顶点间的最短路径,可以调用Dijkstra算法n次,复杂度 O ( n 3 ) O(n^{3}) O(n3),也可以用弗洛伊德算法(Floyd),复杂度也是 O ( n 3 ) O(n^{3}) O(n3),但是形式上看起来简单一点。
参考资料
《数据结构c语言版》 严蔚敏著