Scipy 稀疏矩阵 COO、CSC、CSR

在Scipy包中，存在专门针对稀疏矩阵进行优化存储的函数，分别是COO、CSC和CSR。

之所以要使用稀疏矩阵，是因为计算所使用的数据中会存在很多无效项，所以可以转化存储方式，放弃存储无效数据，存储更多的有效数据，降低计算的复杂度。

在Scipy中有专门用于数学计算优化的package，就是scipy.sparse。而COO、CSC和CSR就是在sparse中定义的函数。

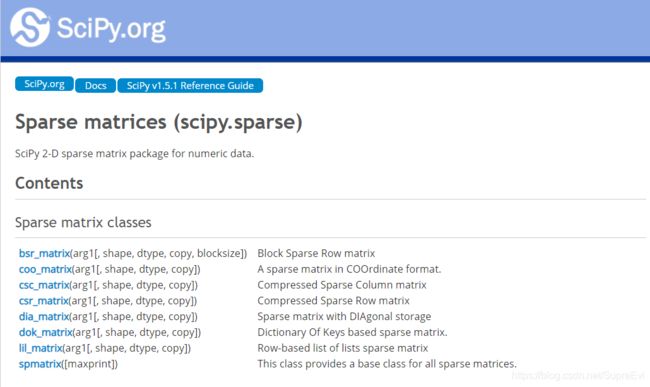
Scipy.sparse官方文档

可以看到在Sqarse matrix classes中存在三个类定义，分别是

Sqarse matrix classes
coo_matrix(arg1[, shape, dtype, copy])	A sparse matrix in COOrdinate format
csc_matrix(arg1[, shape, dtype, copy])	Compressed Sparse Column matrix
csr_matrix(arg1[, shape, dtype, copy])	Compressed Sparse Row matrix

从官方文档的描述上来进行理解，可以得知：

COO是coordinate的缩写，也就是说COO方法就是数据结构中记录稀疏矩阵的方法，即三元组形式。

CSC是压缩存储稀疏矩阵的类，其中的C就是指column，也就是按照列来压缩存储压缩矩阵。

CSR与CSC类似，只不过R是指row，也就是按照行来进行压缩存储。

（1）Coordinate (COO)

>>> row = np.array([0, 3, 1, 0])
>>> col = np.array([0, 3, 1, 2])
>>> data = np.array([6, 5, 7, 8])
>>> sparse.coo_matrix((data, (row, col)), shape=(4, 4)).toarray()
array([[6, 0, 8, 0],
       [0, 7, 0, 0],
       [0, 0, 0, 0],
       [0, 0, 0, 5]])

这是最简单的一种格式，每一个元素需要用一个三元组来表示，分别是（行号，列号，数值），对应上图右边的一列。这种方式简单，但是记录单信息多（行列），每个三元组自己可以定位，因此空间不是最优。

(2)Compressed Sparse Column (CSC)

>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> sparse.csc_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 4],
       [0, 0, 5],
       [2, 3, 6]])

CSC是按列存储一个稀疏矩阵的。其中indptr中的数据代表矩阵中每一列所存的数据在data中的开始和结束的索引，例如这里indptr为[0, 2, 3, 6]，即表示在data中，索引[0, 2)为第一列的数据，索引[2, 3)为第二列的数据，索引[3, 6)为第三列的数据。而indices中的数据代表所对应的data中的数据在其所在列中的所在行数，例如，这里的indices为[0, 2, 2, 0, 1, 2]，表示在data中，数据1在第0行，数据2在第2行，数据3在第2行，数据4在第0行，数据5在第一行，数据6在第2行。从而建立起一个稀疏矩阵。

 

(3)Compressed Sparse Row (CSR)

>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> sparse.csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 2],
       [0, 0, 3],
       [4, 5, 6]])

CSR是按行来存储一个稀疏矩阵的，其原理与CSC类似。indptr中的数据表示矩阵中每一行的数据在data中开始和结束的索引，而indices中的数据表示所对应的在data中的数据在矩阵中其所在行的所在列数。可以看出，在indptr、indices和data三个数组相同的情况下，通过CSC和CSR分别表示出来的矩阵互为转置关系。

 

Notes：

（1）为什么要区分行序和列序

以CSC函数为例

>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> sparse.csc_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 4],
       [0, 0, 5],
       [2, 3, 6]])

需要注意的是，如果是以列序为主，那么data数据的排列就是按照第一列、第二列、第三列的顺序来记录的。

也就是从第一列的第一个元素开始按照列序来生成data。

例子中的data是[1,2,3,4,5,6],这正好是矩阵array按照列序进行读取的顺序。

如果改换成这个形式：

import numpy as np
import scipy as sy 
from scipy import sparse
indptr = np.array([0,2,3,6])
indices = np.array([0,2,2,0,1,2])
data = np.array([2,1,5,3,4,6])
X =sparse.csc_matrix((data, indices, indptr), shape=(3, 3)).toarray()
print(X)

就得出了这个矩阵结果：

[[2 0 3]
 [0 0 4]
 [1 5 6]]

（2）后缀toarray()、tocsc()和tocsr()
确定生成的变量是什么类型的。

后缀

后缀类型	含义
toarray()	转换成
tocsc()	转换成
tocsr()	转换成

代码：

import numpy as np
import scipy as sy 
from scipy import sparse
indptr = np.array([0,2,3,6])
indices = np.array([0,2,2,0,1,2])
data = np.array([2,1,5,3,4,6])
X =sparse.csc_matrix((data, indices, indptr), shape=(3, 3)).tocsr()
print(type(X))

输出：

引用：

https://www.jianshu.com/p/9671c568096d