简介
Dijkstra算法是图算法里求单点源最短路径的一个经典问题。以前在看一些学习材料的时候经常看到它被提起。在将近10年前学习的时候曾经看过一遍,可惜理解的还不够深刻,很快就忘记了。理解一个问题的的基础就是要理解它背后的核心思想。本文对该算法的过程和推导做一个分析,希望能够加深一些印象。
问题分析
这个问题的本身看起来比较简单。就是对于一个我们熟知的图来说,我们指定一个点作为源节点,我们希望能够通过从这个节点出发找到所有其他节点,同时保证从这个节点到其他节点的路径是最短的。也就是说,我们要求这个指定节点到其他所有节点的最短路径。
这个问题本身基于一个前提,我们假定这个图是连通的,即任意两个点可以在图中有连接的路径。而且,对于这种最短路径,我们可以应用于有向图也可以用于无向图。我们这里以有向图为例。
在讨论这个问题之前,我们先看一个更加简化一点的问题,假定我们知道图中的一个源节点,我们先只考虑求它到另外一个特定的节点的最短路径。对于一个图G(E, V)来说,因为它是连通的,假设源节点为s,目的节点为t。从理论上我们可能有多条路径从s到t节点。我们分别命名为s, v1, v2, ...vk, t或者s, w1, w2, ..wj, t等。这样,我们这里从s到t节点的路径长度无非就是以下几个E(s, v1) + E(v1, v2) + ...+E(vk, t),E(s, w1) + E(w1, w2)...+E(wj, t)。我们理想的最短路径那么就是取这些和中间的最小值。
现在,我们再换一个角度来考虑一下这个问题。假定我们有一组节点组成的路径是从s到t节点的最短路径。比如说这组节点分别为s, v1, v2, ...vk, t。那么这组最短路径有什么特性呢?我们会发现,从s到路径中的任何一个节点都是最短路径。为什么呢?假定我们有一组节点wi, wi+1,...vi,通过它的路径比通过v1, v2...vk的路径更短,那么通过它们到达t的路径才是最短的路径,这和我们前面假定s, v1, v2,...vk, t是最短路径相矛盾。所以说,这个依据应该对我们后面的应用很有帮助。
Relax过程
有了前面的一点讨论,我们需要考虑一个典型的情况就是。可能在图里面,我们前面求出来的某个到k点的距离distTo[j]值并不是最小的。当我们后面遍历到另外一个节点的时候,比如j的时候,有一个j到k的边,使得从s点到j再到k的距离比原来计算出来的到k的距离更短。它们满足这么一个关系:
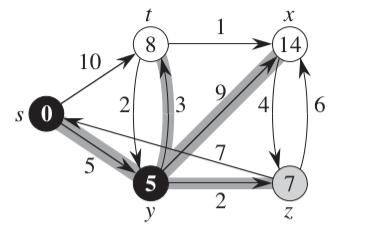
distTo[k] > distTo[j] + weight(j, k)。 显然,我们这个时候就需要做一个调整,这个通过j节点的路径明显更优。于是我们就需要更新这个到k节点的路径长度值。我们设置为distTo[k] = distTo[j] + weight(j, k); 以下图为例:
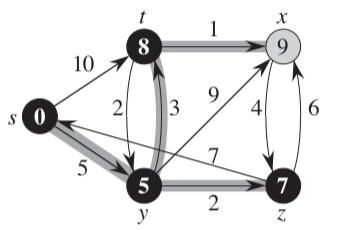
我们可以看到当我们访问到节点y的时候,在它能够直接访问到的关联节点里,它到节点x的距离是9, 在现有的条件下,它们的最短距离可以认为是9。可是当我们访问到节点t的时候,发现从节点y,然后到t再到节点x的时候,他们的总共长度才3+1=4, 比9还要小,于是我们就要将它们的最短距离设置成4。如下图:
这样,我们原来那个从y到x原来那个路径就不再是最短路径了。可以说,这个relax的过程就是用来进行路径优化的过程。我们再考虑一点实现细节相关的问题。假定我们知道从y到t再到x确实是最短路径,可是我们该怎么来表示和记录他们呢?如果我们只是更新一个distTo[]这样的数组,只是知道到那边的距离是多少,可是并不知道它是走的哪条路径啊。这个时候,我们前面讨论的一个特性在这里起作用了。我们其实之需要一个记录边的数组就可以了,假设我们定义为EdgeTo[],在这里,我们只要定义EdgeTo[x]的边就可以了。这里的EdgeTo[x]表示最短路径中,目的节点为x的那个边,在这里是(t, x)。为什么我们不需要记录整个路径呢?因为到t的节点也是最短路径上的啊。我们根据EdgeTo[x] = (t, x)可以倒推到节点t。而节点t对应的最短路径边关系EdgeTo[t] = (y, t),这样不就可以一步步回溯到源节点了么?这里是记录它们的路径的一个比较巧妙的地方。
整体过程
我们有了前面这个relax更新的过程,还有一个需要考虑的就是怎么来推进整个图,来计算到所有节点的最短路径。没有一个推进的方向盲目的运用relax过程肯定不行。我们考虑到,最开始是从一个源节点开始的。我们可以考虑通过它最开始能够直接关联的节点,然后一步步往外面推。对于和它直接关联的节点,我们可以得到它们的权值。而最开始没有直接关联的,假定他们之间的权值为无穷大。以后每次通过它关联到新的节点时,我们就来利用relax过程比较。使得每次只要能够被遍历到的节点,它到源节点的权值是最小的。
我们的思路到这一步的时候,会发现这个从一个节点扩展的思路和前面一篇文章讲Prim算法的思路很近似。其实,Dijkstra算法和Prim算法的一个唯一的差别就是Prim算法扩展的时候,每次把新关联的边加入到集合中之后是取出关联到这个集合中来的权值最小的边,而这里是要取到源节点长度最短的边。我们结合一个示例来分析一下整个的过程:
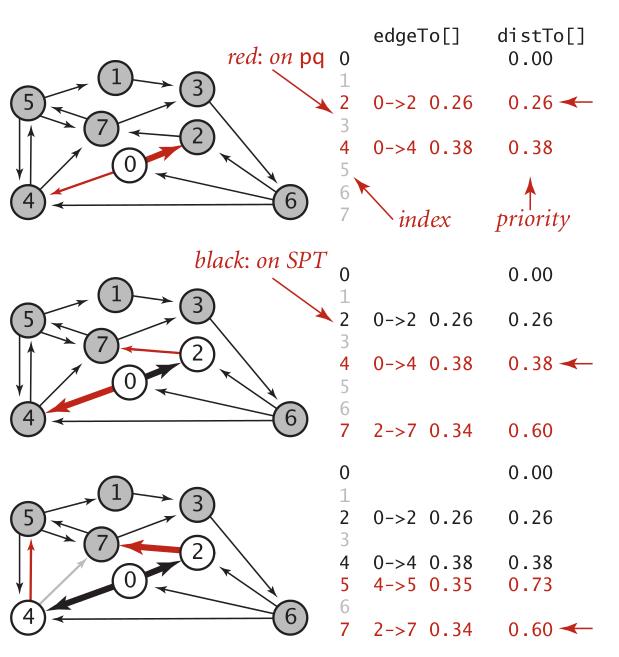
在图中,我们从节点0开始,它相邻的节点是2和4, 对应的边权值分别为0.26和0.38。于是按照前面的过程,我们首先将0->2, 0->4这两个边加入到一个集合里。然后得到从0到2和0到4的距离分别为0.26和0.38。这样,我们取到0节点最短的节点的边作为最短路径。于是我们确定了边0->2。接着再从节点2进行扩展。2关联的节点有7, 我们将边2->7加入集合。因为2->7的权值是0.34,于是从0到7的距离是0.60。这个时候,集合里距离最短的是0->4的边,于是我们考察节点4, 它关联的点分别为5和7。4到7节点的距离加上0到4节点的距离的值比原来计算出来的0.60要大,于是这个边不考虑。而4->5的边权值为0.35,到0节点的权值则为0.73 。我们可以将它放入集合中。
所以前面这个过程就是我们不断选择到源节点最短的边,根据这个边所关联的节点再引入新关联的边进来。
实现细节
通过前面的讨论,我们知道需要的一些数据结构主要有以下几个:
distTo数组,用来保存从源节点到目的节点的当前最短距离。
edgeTo数组,保存指向某个节点的边,关键是这个边是构成最短路径中的那个。
一个集合结构,在这个集合里,我们将选取的候选长度放到里面。每次从里面选取最小的值,同时,在relax更新一些distTo值的时候,也更新集合里面的信息。
另外,我们还有两个基本的定义,就是边和图的结构定义。这里,我们考虑有向图,所以要专门定义一个有向图的结构,它们的边数据类型也不一样。我们一个个的看过来。
有向图
我们定义有向图的话,肯定里面的边是有一个起点和目的点的。于是我们可以很容易的定义一个边的结构如下:
public class DirectedEdge {
private final int v;
private final int w;
private final double weight;
public DirectedEdge(int v, int w, double weight) {
if(v < 0) throw new IndexOutOfBoundsException();
if(w < 0) throw new IndexOutOfBoundsException();
if(Double.isNaN(weight)) throw new IllegalArgumentException();
this.v = v;
this.w = w;
this.weight = weight;
}
public double weight() {
return weight;
}
public int from() {
return v;
}
public int to() {
return w;
}
public String toString() {
return String.format("%d->%d %.2f", v, w, weight);
}
}这部分的实现很直观,from()表示边的起点,to()表示目的节点。
除了这部分以外,我们对有向图的定义也很容易实现,基于前面对无向图的定义稍微做一点修改。主要变更的地方就是i在每次增加一个边的时候不是原来关联到两个节点,而只是一个节点就可以了。下面是详细的实现:
import java.util.List;
import java.util.ArrayList;
import java.util.LinkedList;
public class EdgeWeightedDigraph {
private final int vertices;
private int edges;
private List> adj;
public EdgeWeightedDigraph(int vertices) {
if(vertices < 0)
throw new IllegalArgumentException();
this.vertices = vertices;
this.edges = 0;
adj = new ArrayList>();
for(int i = 0; i < vertices; i++)
adj.add(new LinkedList());
}
public int getVertices() {
return vertices;
}
public int getEdges() {
return edges;
}
public void addEdge(DirectedEdge e) {
adj.get(e.from()).add(e);
edges++;
}
public Iterable adj(int vertice) {
if(vertice < 0 || vertice >= vertices)
throw new IndexOutOfBoundsException();
return adj.get(vertice);
}
public Iterable edges() {
List list = new LinkedList();
for(int v = 0; v < vertices; v++)
for(DirectedEdge e : adj.get(v))
list.add(e);
return list;
}
public int outdegree(int v) {
if(v < 0 || v >= vertices)
throw new IndexOutOfBoundsException();
return adj.get(v).size();
}
} 在确定了图的定义思路之后,这部分代码看起来就很简单了,没什么好说的。
最小权值集合
老实说,这也许算是最麻烦的地方了。在前面我们提到过要利用一个集合来保存到源节点当前最短路径的值。从这个角度来看的时候,我们可以想到用最小堆,也就是PriorityQueue。可是目前的PriorityQueue只支持对元素的加入和删除,我们可以保证每次remove的时候是拿的最小的值,add方法加入的值也可以很好的组织。可问题的关键是我们怎么来修改堆里一个指定的值呢?而且修改后还要保证整个堆维持最小堆的特性。另外,我们放在堆里的如果只是一个纯粹的distTo[i]的值还是不够的。因为光知道这个值我们还是不能确定它到底是对应的从源节点到哪个节点。所以还必须定义一个结构把关联的节点也包含进去。这么说起来有点让人难以明白,我们还是列一个详细表来描述一下这个数据结构应该支持的功能。
| 方法名 | 说明 |
| boolean contains(int w) | 这个集合里是否包含有指定节点对应的distTo距离值。 |
| void change(int w, double dist) | 修改这个集合里对应节点的distTo值。 |
| void insert(int w, double dist) | 在集合里加入对应节点w的distTo值。 |
| Item remove() | 从堆里移除最小的元素。 |
| boolean isEmpty() | 判断堆是否还包含有元素。 |
总的来说,就这5个方法。目前的PriorityQueue支持remove, isEmpty, insert这3个方法。对其他几个方法不支持。看来,我们直接用PriorityQueue的思路行不通了。我们能否可以借用一部分PriorityQueue的特性然后自己增强一部分呢?
实际上,在解决这个问题的时候,我们有两个思路。如果我们还记得之前讨论堆排序和建堆的文章里说过怎么变更一个节点的值然后再调整堆的话,我们是完全可以自己定义一个增强类型的PriorityQueue,然后在里面增加这几个功能。这相当于重新实现一个类似于PriorityQueue的结构。这个思路的详细实现可以见该链接。这里重点讨论另外一种思路。就是借用PriorityQueue,在它的基础上增加一个辅助的结构来实现同样的功能。
我们的思路如下:
1. 既然我们需要通过contains(w)来检查是否包含有对应的路径长度值,我们可以用一个最简单的数组assList[]来保存可以放入堆里的对象。这样每次检查contains(w)的时候只要看这个数组里索引为w的元素是否为空。不为空则表示有元素。
2. 我们放入堆里的元素也需要倒过来知道它是对应到哪个节点的。一个最不济的办法,我增加一个对应到哪个节点的成员项,表示对应节点的值。而且每次将路径长度值加入到堆里的时候我们可以知道对应到哪个节点和长度,所以这也是很自然的事情。
按照这两点讨论我们可以定义一个如下的结构:
import java.util.PriorityQueue;
public class EnhancedPriorityQueue {
private PriorityQueue- queue;
private Item[] assList;
public static class Item implements Comparable
- {
private int s;
private Double t;
public Item(int s, Double t) {
this.s = s;
this.t = t;
}
public int getSource() {
return s;
}
public double getT() {
return t;
}
public void setT(Double t) {
this.t = t;
}
public int compareTo(Item other) {
return t.compareTo(other.getT());
}
}
public EnhancedPriorityQueue(int max) {
queue = new PriorityQueue
- ();
assList = new Item[max];
}
public void change(int w, Double dist) {
queue.remove(assList[w]);
assList[w].setT(dist);
queue.add(assList[w]);
}
public void insert(int w, Double dist) {
assList[w] = new Item(w, dist);
queue.add(assList[w]);
}
public boolean isEmpty() {
return !(queue.size() > 0);
}
public Item remove() {
Item item = queue.remove();
int i = item.getSource();
assList[i] = null;
return item;
}
public boolean contains(int w) {
return assList[w] != null;
}
}
代码里定义的内部类Item主要用来关联节点和路径长度值。而类里定义的Item[]列表用来指向所有加入到堆里的Item元素。因为PriorityQueue需要对里面的元素比较并选择最小的,所以这里的Item实现了Comparable接口。通过这种方式,我们只需要做一些增强而不用重写一个PriorityQueue的大部分功能。另外,我们借用了一些PriorityQueue的功能,对于元素的更新,我们首先根据关联关系将元素取出来,然后修改后再加入到堆中,实现这个修改的效果。
合并起来
现在剩下的这部分就是Dijkstra算法的主要内容了。我们详细的实现代码如下:
import java.util.Stack;
public class DijkstraSP {
private DirectedEdge[] edgeTo;
private double[] distTo;
private EnhancedPriorityQueue pq;
public DijkstraSP(EdgeWeightedDigraph g, int s) {
edgeTo = new DirectedEdge[g.getVertices()];
distTo = new double[g.getVertices()];
pq = new EnhancedPriorityQueue(g.getVertices());
for(int v = 0; v < g.getVertices(); v++)
distTo[v] = Double.POSITIVE_INFINITY;
distTo[s] = 0.0;
pq.insert(s, 0.0);
while(!pq.isEmpty())
relax(g, pq.remove().getSource());
}
private void relax(EdgeWeightedDigraph g, int v) {
for(DirectedEdge e : g.adj(v)) {
int w = e.to();
if(distTo[w] > distTo[v] + e.weight()) {
distTo[w] = distTo[v] + e.weight();
edgeTo[w] = e;
if(pq.contains(w))
pq.change(w, distTo[w]);
else
pq.insert(w, distTo[w]);
}
}
}
public double distTo(int v) {
return distTo[v];
}
public boolean hasPathTo(int v) {
return distTo[v] < Double.POSITIVE_INFINITY;
}
public Iterable pathTo(int v) {
if(!hasPathTo(v))
return null;
Stack path = new Stack();
for(DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()]) {
path.push(e);
}
return path;
}
} 我们在构造函数里首先将distTo数组初始化,对于源节点来说,所有到其他节点的距离为无穷大。然后类似于一个图的广度优先遍历过程一样,将节点加入到优先队列里。以后每次从队列里取元素,调用relax过程来更新权值。所有详细的代码和对应的运行结果可以在附件代码中找到。
总结
找到一个点,然后通过它所关联的边向外扩展到其它的边。然后根据已有的信息不断更新到各节点的距离。每次取到源节点距离最短的节点,继续扩张。这样不断重复原来的过程。这就是Dijkstra算法。它的难点在于要定义这么一个结构,既要有优先队列的特性又能支持查找和更新。
参考材料
Introduction to algorithms
Algorithms
http://algs4.cs.princeton.edu/44sp/IndexMinPQ.java.html