数据结构算法-插入排序
插入排序算法有两种,一种是直接插入排序,一种是折半插入排序
算法分析:1.当元素的初始序列为正序时,仅外循环要进行n-1趟排序且每一趟只进行一次比较,没有进入if语句不存在元素之间的交换(移动)。此时比较次数(Cmin)和移动次数(Mmin)达到最小值。
Cmin = n-1Mmin = 0;
此时时间复杂度为O(n)。
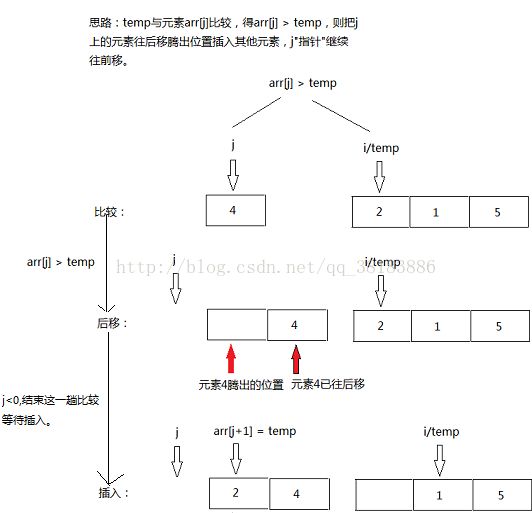
2.当元素的初始序列为反序时,每趟排序中待插入的元素都要和[0,i-1]中的i个元素进行比较且要将这i个元素后移(arr[j+1] = arr[j]),i个元素后移移动次数当然也就为i了,再加上temp = arr[i]与arr[j+1] = temp的两次移动,每趟移动的次数为i+2,此时比较次数(Cmin)和移动次数(Mmin)达到最小值。
Cmax = 1+2+...+(n-1) = n*(n-1)/2 = O(n2)
Mmax = (1+2)+(2+2)+...+(n-1+2) = (n-1)*(n+4)/2 = O(n2) (i取值范围1~n-1)
此时时间复杂度为O(n2)。
3.在直接插入排序中只使用了i,j,temp这3个辅助元素,与问题规模无关,所以空间复杂度为O(1).
4.在整个排序结束后,即使有相同元素它们的相对位置也没有发生变化,
如:5,3,2,3排序过程如下
A--3,5,2,3
B--2,3,5,3
C--2,3,3,5
void InsertSort(int a[], int n)
{
for(int i= 1; i折半插入排序:
算法的基本过程:
1)计算 0 ~ i-1 的中间点,用 i 索引处的元素与中间值进行比较,如果 i 索引处的元素大,说明要插入的这个元素应该在中间值和刚加入i索引之间,反之,就是在刚开始的位置 到中间值的位置,这样很简单的完成了折半;
2)在相应的半个范围里面找插入的位置时,不断的用(1)步骤缩小范围,不停的折半,范围依次缩小为 1/2 1/4 1/8 .......快速的确定出第 i 个元素要插在什么地方;
3)确定位置之后,将整个序列后移,并将元素插入到相应位置。
折半插入排序过程:
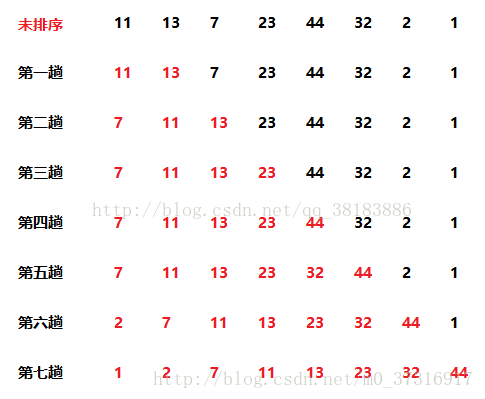
第一趟:按上述代码的流程分析,从A[2]开始计算,{11}是一个已排序子表,按关键字13进行折半查找它的位置,代码的上半部分查找该元素元素应该插入的位置为A[2],所以下半部分并不需要移动元素,已排序子表为{11,13}
第二趟:从A[3]开始计算,low=1,high=2,mid=1,因为7<11,所以high=2-1=1;第二次循环mid=1,7<11,high=0,循环不满足条件,此时开始移动元素;要移动的元素范围为A[1]到A[2],A[1]=7。
第三趟第四趟依此类推…..(只要记住一点,先折半查找元素的应该插入的位置,然后统一移动应该移动的元素,再将这个元素插入到正确的位置)
void BinaryInsertSort(int array[],int n)//传递数组和数组元素个数
{
int i,j,mid,low,high,temp;
for(i = 1; i < n; ++i) //我看了一些其他人写得折半插入算法是从下标1开始的,i = 2;i <=n,并将array[i]存储到array[0]
{
temp = array[i];//把第i+1个元素赋值给temp(数组从下标0开始)
low = 0;//初始化low,array[low]代表数组中第1个元素
high = i;//初始化high,array[high]代表已插入的最后一个元素
while(low <= high) //不断的折半1/2 1/4 ....
{
mid = (low + high) / 2;//计算中间位置
if (temp > array[mid])
{
//插入值大于中间值
low = mid + 1;
}
else
{
//插入值小于中间值
high = mid - 1;
}
}
for(j=i-1; j >= low; --j)
{
//将需要移动的数组向后移
array[j+1] = array[j];
}
//将值插入到指定位置
array[low] = temp;
}
}折半插入排序基本思想和直接插入排序一样,区别在于寻找插入位置的方法不同,折半插入排序采用折半查找法来寻找插入位置。折半查找法只能对有序的序列使用。基本思想就是查找插入位置的时候,把序列分成两半(选择一个中间数mid),如果带插入数据大于mid则到右半部分序列去在进行折半查找;反之,则到左半部分序列去折半查找。
折半插入排序在记录移动次数上和直接插入排序是一样,所以算法时间复杂度也是一样,只是在寻找插入位置的时候可能会节约相当多的时间。