单源最短路径——Dijksrta及其他
温馨提示:程序框中的注释比截图中全
原题
https://www.luogu.org/problemnew/show/P3371
https://www.luogu.org/problemnew/show/P4779
无负环用Dijkstra,有负环用SPFA。实现方式有邻接矩阵和邻接表,数据量太大时用邻接表。Dijkstra要比SPFA快。dijkstra(O(nlogn))、SPFA(O(KE))。考场一般不推荐用SPFA
!!!pat撑死就考个迪杰斯特拉,哦!老迪牛逼!
模板参考算法笔记,尽量用邻接表来做,邻接矩阵可能会被卡。
推荐方法零(最快)。
方法零:前向星+优先队列堆优化+Dijkstra
(方法零比方法四少了两个数组,少了初始化及其他步骤的时间,另外最重要的是,方法零的Dijkstra()中的优先队列同时存点号和权值,当该点权值发生变化时continue,这不是一种剪枝,而是在矫正路径,同时避免了废点的计算。方法四用标记数组tag[]标记是否访问,可能会发生错误:在访问u点后不能再次访问该点,但是有一条更短的路径可以到达u但此时已经不能再次访问u点进行计算,即当路径有后续更新时方法四不能再进行更新。方法零用优先队列每次弹出时作比较的方法避免了这种后续更新出错的情况,在队列空之前都可以进行更新。所以在数据更严密时,严格意义上方法四是错误的,方法一、方法二同理错误!)
#include
#define re register
using namespace std;
inline int read()//快读
{
int x=0,w=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')w=-1;c=getchar();}
while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
return x*w;
}
struct Edge{
int v,w,nxt;
}e[500010];
int head[100010],cnt=0;
inline void addedge(int u,int v,int w){
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
//nxt记录的是同起点的之前一条边的cnt值,cnt唯一标识一条边
head[u]=cnt;//cnt相当于邻接表的下标
}
int n,m,s;
int dis[100010];//更新最新的权值,与队列中的权值有可能不同
struct node{
int u,d;//重载
bool operator<(const node&rhs) const{
//固定格式 用地址进行操作 rhs代表第二个(右边的)数据
return d>rhs.d;}//从大到小排序即值大的优先级低,优先级高的值小
//堆顶优先级最高,序列中靠前(左)的优先级低
};
inline void Dijkstra(){
for(re int i=1;i<=n;i++) dis[i]=2147483647;//重要的初始化
dis[s]=0;//重要的初始化
priority_queue Q;//优先队列 (小根堆)
Q.push((node){s,0});// 向队列Q中压入node型元素,该元素中u=s,d=0
while(!Q.empty()){
node fr=Q.top();Q.pop();
//每次弹出的都是权值最小的点,但是队列中该点会有重复但权值是不同的即存在废点,
//针对这种情况只有方法零进行了优化而方法四没有
int u=fr.u,d=fr.d;
if(d!=dis[u]) continue;//这不是一种剪枝,而是矫正路径,方法四中用的是标记数组tag[]
//到达该u点的路径被优化过,d(fr.d,曾经的dis[d]与现在的dis[d]值不相同)
//不能再用其进行计算
for(re int i=head[u];i;i=e[i].nxt){
//nxt记录的是同起点的之前一条边的cnt值,是一个回溯的过程
int v=e[i].v,w=e[i].w;
if(dis[u]+w 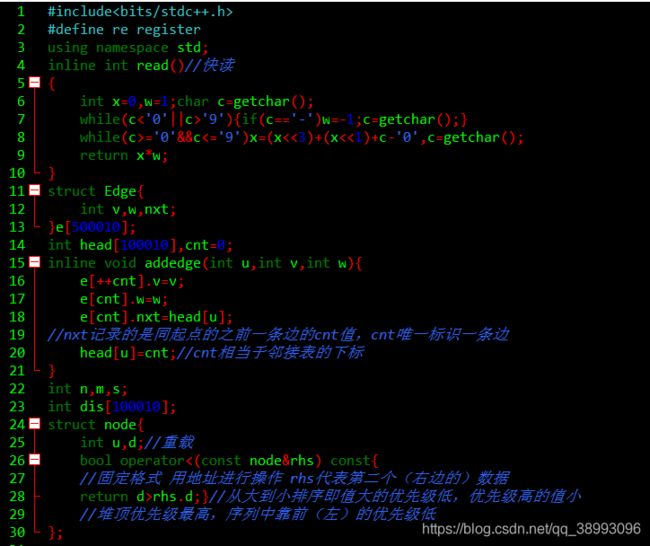
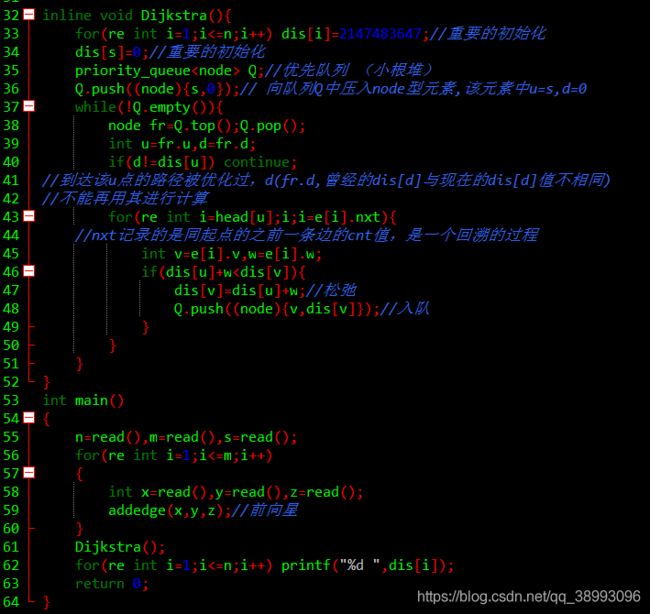
方法一:邻接表+Dijkstra(算法笔记的模板未使用优先队列(堆优化),不能通过P4779)
#include
using namespace std;
const int maxv=100010;//点的最大值
const int INF=2147483647;
struct Node{
int v,dis;
};
vectorAdj[maxv];//用变长数组来实现邻接表
int n,m,s;
int d[maxv];//起点到达各点的最短距离
bool vis[maxv]={false};//标记某点是否被访问过
inline int read()//读入优化
{
int x=0;
char c=getchar();
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return x;
}
inline void write(int x)//输出优化
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
inline void Dijkstra(int s)
{
//fill(d,d+maxv,INF);
memset(d,INF,sizeof(d));
d[s]=0;//重要初始化
for(register int i=1;i<=n;i++){
int u=-1,MIN=INF;
for(register int j=1;j<=n;j++){//找到未访问的顶点中d[u]最小的 ,就是路径已经最优的
//方法零方法四在此处利用优先队列进行了堆优化
if(vis[j]==false&&d[j]>n>>m>>s;
for(register int i=1;i<=m;i++)
{
x=read();xx.v=read();xx.dis=read();
Adj[x].push_back(xx);//Adj[]数组的元素变量类型为Node
}
/*for(i=1;i<=3;i++)
{
for(j=0;j 

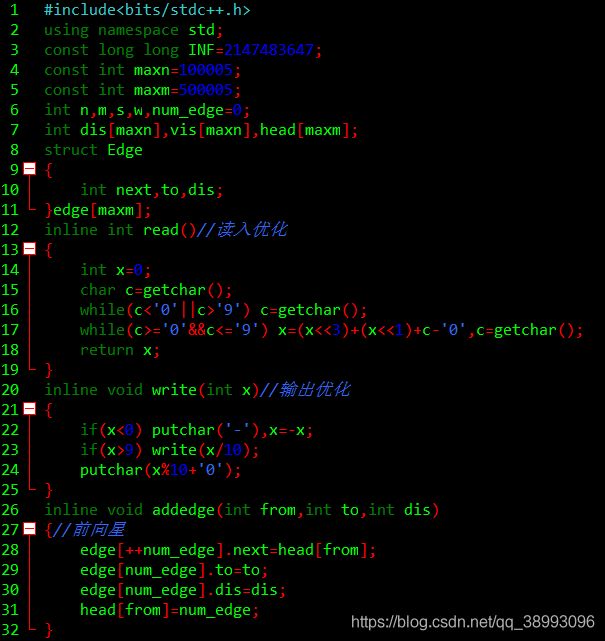
方法二:邻接表+SPFA
(SPFA可以处理有负权的情况,Dijkstra不能)
#include
using namespace std;
const long long INF=2147483647;
const int maxn=100005;
const int maxm=500005;
int n,m,s,w,num_edge=0;
int dis[maxn],vis[maxn],head[maxm];
struct Edge
{
int next,to,dis;
}edge[maxm];
inline int read()//读入优化
{
int x=0;
char c=getchar();
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return x;
}
inline void write(int x)//输出优化
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
inline void addedge(int from,int to,int dis)
{//前向星
edge[++num_edge].next=head[from];
edge[num_edge].to=to;
edge[num_edge].dis=dis;
head[from]=num_edge;
}
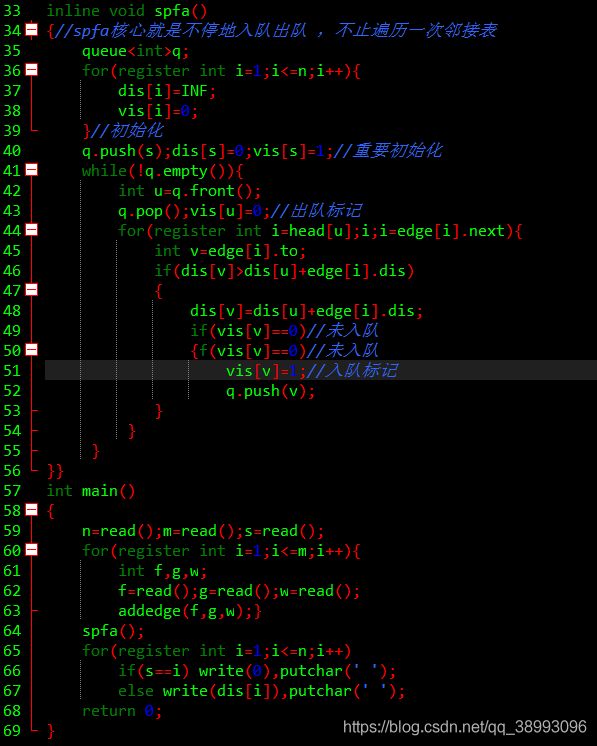
inline void spfa()
{//spfa核心就是不停地入队出队 ,不止遍历一次邻接表
queueq;
for(register int i=1;i<=n;i++)
{
dis[i]=INF;
vis[i]=0;
}//初始化
q.push(s);dis[s]=0;vis[s]=1;//重要初始化
while(!q.empty())
{
int u=q.front();
q.pop();vis[u]=0;//出队标记
for(register int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(dis[v]>dis[u]+edge[i].dis)
{
dis[v]=dis[u]+edge[i].dis;
if(vis[v]==0)//未入队
{
vis[v]=1;//入队标记
q.push(v);
}
}
}
}}
int main()
{
n=read();m=read();s=read();
for(register int i=1;i<=m;i++)
{
int f,g,w;
f=read();g=read();w=read();
addedge(f,g,w);
}
spfa();
for(register int i=1;i<=n;i++)
if(s==i) write(0),putchar(' ');
else write(dis[i]),putchar(' ');
return 0;
}
#include
using namespace std;
const int maxn=100005,maxm=500005,INF=2147483647;
long long dis[maxn];
int u[maxm],v[maxm],w[maxm],n,m,s,check;
//maxn是点的最大个数,maxm是边的最大个数
int read()//读入优化
{
int x=0;
char c=getchar();
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return x;
}
void write(int x)//输出优化
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
int main()
{
int s,check;
int x,y,z;
n=read(),m=read(),s=read();
for(int i=1;i<=m;i++)
{
u[i]=read(),v[i]=read(),w[i]=read();
}
memset(dis,INF,sizeof(dis);
//for(int j=1;j<=n;j++)dis[j]=INF;//重要赋值
dis[s]=0;
for(int k=1;k<=n-1;k++)//k-1条边
{
check=0;
for(int i=1;i<=m;i++)//遍历所有边
{
if(dis[v[i]]>dis[u[i]]+w[i])
{
dis[v[i]]=dis[u[i]]+w[i];
check=1;
}
}
if(check==0) break;//没有边了,边的个数小于n-1
}
for(int i=1;i<=n;i++) write(dis[i]),putchar(' ');
return 0;
}

方法四(隐蔽性错误,洛谷P4779无法通过):前向星+优先队列堆优化+Dijkstra
(本方法用标记数组tag[]标记是否访问,可能会发生错误:在访问u点后不能再次访问该点,但是有一条更短的路径可以到达u但此时已经不能再次访问u点进行计算,方法零避免了这种情况)
#include
using namespace std;
const int maxn=100005,maxm=500005,inf=2147483647;
//maxn是点的最大个数,maxm是边的最大个数
int n,m,cnt;
bool tag[maxn];//访问标记
int head[maxm],nxt[maxm],v[maxm];//v是对应边可以到达的点
int w[maxm],dist[maxn];//w是权值,dist是源点到每个点的最短距离
int read()//读入优化
{
int x=0;
char c=getchar();
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return x;
}
void write(int x)//输出优化
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
struct cmp//优先队列排序的一种固定格式
{
bool operator()(int x,int y)//重载操作符
{
return dist[x]>dist[y];//>表示越往下越大即小根堆,故<是大根堆
}
};
void addline(int x,int y,int z)//前向星就是邻接表
{
v[cnt]=y;//v存后驱
w[cnt]=z;//w存权值
nxt[cnt]=head[x];//nxt存前驱
head[x]=cnt++;
return;
}
void dijkstra(int s)
{
priority_queue,cmp>Q;//固定格式 Q存放点号
//Q中存的是点号,但是比较的是dist[]的值
while(!Q.empty()) Q.pop();//队列清空 初始化
dist[s]=0;//记录花费
Q.push(s); //源点入队
while(!Q.empty())
{
int x=Q.top();
Q.pop();
if(!tag[x])//剔除队列中的废点
{
tag[x]=true;//每个节点只访问一次,检索以该节点为起点的所有边
for(int i=head[x];i!=-1;i=nxt[i])
{
int y=v[i];//y代表对应边可以到达的点
dist[y]=min(dist[y],dist[x]+w[i]);
Q.push(y);//类似于层序遍历
}
}
}
}
int main()
{
int s;
n=read(),m=read(),s=read();
memset(head,-1,sizeof(head));//重要的初始化
memset(tag,0,sizeof(tag));
for(int i=1;i<=m;i++)//链式前向星
{
int x,y,z;
x=read(),y=read(),z=read();
addline(x,y,z);
}
for(int j=1;j<=n;j++)dist[j]=inf;//重要赋值
dijkstra(s);
for(int i=1;i<=n;i++) write(dist[i]),putchar(' ');
return 0;
}