MATLAB 离散傅里叶变换（DFT）、逆离散傅里叶变换（IDFT）、快速傅里叶变换（FFT）的实现

离散傅里叶变换（DFT）、逆离散傅里叶变换（IDFT）的实现

代码如下，其中xn为时序序列

clc;clear;
xn=[7,6,5,4,3,2];
Xk=dft(xn,6);
x=idft(Xk,6);

subplot(2,2,1);stem(0:5,abs(Xk),'filled');
axis([0,5,0,1.1*max(abs(Xk))]);
title('x[n]经DFT后的幅度');xlabel('频率w');ylabel('幅度');

subplot(2,2,2);stem(0:5,angle(Xk),'filled');
axis([0,5,1.1*min(angle(Xk)),1.1*max(angle(Xk))]);
title('x[n]经DFT后的相角');xlabel('频率w');ylabel('相角');

subplot(2,2,3);stem(0:5,xn,'filled');
axis([0,5,0,1.1*max(xn)]);
title('原信号x[n]');xlabel('时间n');ylabel('幅度');

subplot(2,2,4);stem(0:5,abs(x),'filled');
axis([0,5,0,1.1*max(abs(x))]);
title('原信号x[n]经DFT与IDFT的信号');xlabel('时间n');ylabel('幅度');

function [Xk]=dft(xn,N)
n=0:N-1;
k=0:N-1;
Xk=xn*exp(-j*2*pi/N).^(n'*k);%n'为n的转置

function [xn]=idft(Xk,N)
n=0:N-1;
k=0:N-1;
xn=(Xk*exp(j*2*pi/N).^(n'*k))/N;

快速傅里叶变换（FFT）

可直接使用fft函数，但若需要获取信号的幅值频谱和相位频谱，则需要进行修正，参见代码中的注释：

clear;

Fs=256; %采样频率(Hz)
N=256;  %FFT采样点数,为了方便进行FFT运算，通常N取2的整数次方
n=256; %数据点数
t=[0:1/Fs:n/Fs]; %采样时刻范围，共N个点

%信号:频率(Hz)分别为50、75;幅度分别为3、1.5,相位(度)分别为-30、90;直流分量幅度为2
S=2+3*cos(2*pi*50*t+pi*(-30)/180)+1.5*cos(2*pi*75*t+pi*90/180);
subplot(2,2,1);
plot(S);title('原始信号');

subplot(2,2,2);
Y=fft(S,N); %做FFT变换(N位)
Ayy=(abs(Y)); %取模
% plot(Ayy(1:N)); %显示原始的FFT模值结果
plot(abs(Y));
title('FFT 模值');
text(1,550,'设原始信号的峰值为A(2(0)、3(50)、1.5(75))，那么FFT的结果的每个点（除了第一个点直流分量之外）');
text(1,500,'的模值就是A的N/2(128)倍。而第一个点就是直流分量，它的模值就是直流分量的N(256)倍');
text(1,450,'由于FFT结果的对称性，通常我们只使用前半部分的结果，即小于采样频率一半的结果');

%注：当FFT采样点数N和数据点数n不同时，还需除N/n才能得到真实的幅度
subplot(2,2,3);
Ayy=Ayy/(N/2);   %换算成实际的幅度
Ayy(1)=Ayy(1)/2;
F=([1:N]-1)*Fs/N; %换算成实际的频率值
plot(F(1:N/2),Ayy(1:N/2));   %显示换算后的FFT模值结果
title('幅度-频率曲线图');

subplot(2,2,4);
Pyy=[1:N/2];
for i=1:N/2
    Pyy(i)=phase(Y(i)); %计算相位
    %Pyy(i)=angle(Y(i)); %计算相位
    Pyy(i)=Pyy(i)*180/pi; %换算为角度制
end;
plot(F(1:N/2),Pyy(1:N/2));   %显示相位图
title('相位-频率曲线图');

注1：某点n所表示的频率为：Fn=(n-1)*Fs/N，Fn所能分辨到的最小频率间隔为Fs/N

注2：进行FFT的信号为S，如需用于处理其它信号，直接替换该变量即可

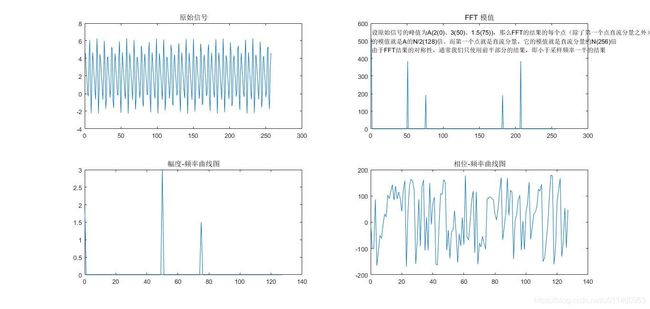
附运行结果，可对照代码理解：

 

转载注明出处：https://blog.csdn.net/csyzcyj/