排序算法学习
前言
参考文章:http://blog.csdn.net/hguisu/article/details/7776068
文章中对算法的解释非常详细,这里只做个人总结和部分算法代码 使用的平台为unity,用c#编写 ,其中代码中涉及的数学方法为unity封装后的方法
插入排序
直接插入排序
///
/// 直接插入排序 (使用List结构)
///
///
/// Sort_Zhijiecharu(List data)
{
//从小到大
for (int i = 1; i < data.Count; i++)
{
int temp = data[i];
int j = i - 1;
if (data[i]< data[i-1])// 如果有调整需要
{
while (temp < data[j])//向前遍历,一直找到比当前元素小的数的下标
{
j--;
if (j < 0) break;//防止下标越界
}
data.RemoveAt(i);
data.Insert(j+1, temp);//将当前元素,插入到后面
}
}
return data;
} 希尔排序
///
/// 希尔排序
///
///
///
/// 希尔排序中使用到的直接插入
///
///
/// 下标的增量 直接插入排序dk=1
/// 选择排序
简单选择排序
///
/// 简单排序
///
///
/// 堆排序
///
/// 调整为大顶堆(或 小顶堆)
///
/// 数组
/// 父节点
/// 数组长度
void HeapAdjust(int[] H, int parent, int length)
{
//构建一个大顶堆,即堆顶为最大元素
int tmp = H[parent];
int child = 2 * parent + 1; //左孩子结点的位置。(i+1 为当前调整结点的右孩子结点的位置)
while (child < length)//经过循环,保证以H[parent]为根结点的子数为一个大顶堆
{
if (child + 1 < length && H[child] < H[child + 1])
{ //如果右孩子大于左孩子(找到比当前待调整结点大的孩子结点)
child++;
}
if (H[parent] < H[child])
{ //如果较大的子结点大于父结点
H[parent] = H[child]; // 那么把较大的子结点往上移动,替换它的父结点
parent = child; // 重新设置parent,即待调整的下一个结点的位置
child = 2 * parent + 1;
}
else
{ //如果当前待调整结点大于它的左右孩子,则不需要调整,直接退出
break;
}
H[parent] = tmp;//当前待调整的结点放到比其大的孩子结点位置上
}
}
///
/// 创建初始堆
///
///
///
void BuildingHeap(int[] H, int length)
{
//最后一个有孩子的节点的位置 i= (length -1) / 2
for (int i = (length - 1) / 2; i >= 0; --i)
{
HeapAdjust(H, i, length);
}
}
///
/// 堆排序
///
///
///
void Sort_Heap(int[] H, int length)
{
//初始堆
BuildingHeap(H, length);
//从最后一个元素开始对序列进行调整
for (int i = length - 1; i > 0; --i)
{
//交换堆顶元素H[0]和堆中最后一个元素
int temp = H[i]; H[i] = H[0]; H[0] = temp;
//每次交换堆顶元素和堆中最后一个元素之后,都要对堆进行调整
HeapAdjust(H, 0, i);
}
}交换排序
冒泡排序
///
/// 冒泡排序
///
///
/// 快速排序
///
/// 快速排序
///
///
///
///
void Sort_Quick(int[] a, int low, int high)
{
if (low < high)
{
int privotLoc = Partition(a, low, high); //将表一分为二
Sort_Quick(a, low, privotLoc - 1); //递归对低子表递归排序
Sort_Quick(a, privotLoc + 1, high); //递归对高子表递归排序
}
}
int Partition(int[] a, int low, int high)
{
int privotKey = a[low];//基准元素
int temp = 0;
while (low < high)
{
//从表的两端交替地向中间扫描
while (low < high && a[high] >= privotKey) --high;//从high 所指位置向前搜索,至多到low+1 位置。将比基准元素小的交换到低端
//位置互换
temp = a[high];
a[high] = a[low];
a[low] = temp;
while (low < high && a[low] <= privotKey) ++low;
//位置互换
temp = a[high];
a[high] = a[low];
a[low] = temp;
}
return low;
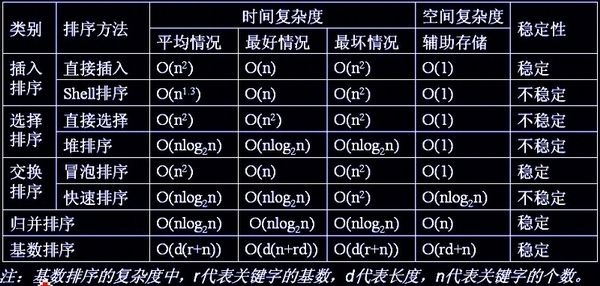
}时间复杂度
稳定性
排序算法的稳定性:若待排序的序列中,存在多个具有相同关键字的记录,经过排序, 这些记录的相对次序保持不变,则称该算法是稳定的;
若经排序后,记录的相对次序发生了改变,则称该算法是不稳定的。
稳定性的好处:排序算法如果是稳定的,那么从一个键上排序,然后再从另一个键上排序,第一个键排序的结果可以为第二个键排序所用。
基数排序就是这样,先按低位排序,逐次按高位排序,低位相同的元素其顺序再高位也相同时是不会改变的。另外,如果排序算法稳定,可以避免多余的比较;
如何选择排序算法
排序算法简单的讲分为两种 空间换时间,时间换空间
根据数据量的多少,数据量的大小,排序速度要求,内存空间大小,稳定性要求,
具体内容 上述文章最后有讲,比较详细