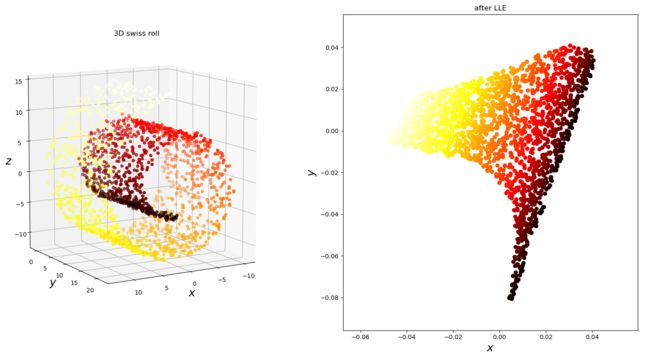
局部线性嵌入(LLE)算法的详细推导及Python实现
局部线性嵌入(Local Linear Embedding, LLE)算法是一种经典的流形学习算法,不同于等度量映射(Isometric Mapping, Isomap)算法考虑结点的全局连接信息,LLE算法只考虑每个结点的k近邻信息,所以速度比Isomap快很多。LLE的思想如下图所示,LLE在低维空间保持了原始高维空间样本邻域内的线性关系,这也是局部线性的一个最直接的解释:高维数据在局部上具有欧式空间的性质,满足线性相关性。
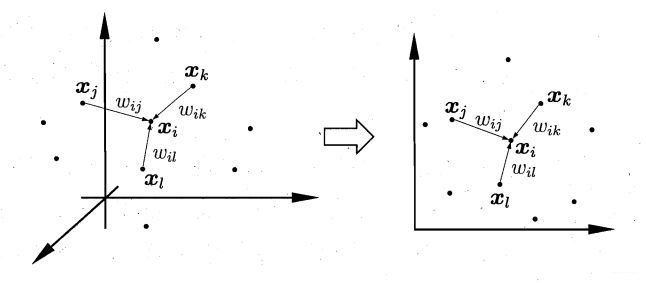
给定LLE算法的输入 χ = { x 1 , x 2 , . . . , x N } ∈ R D × N \chi=\{x_1, x_2,...,x_N\}\in R^{D\times N} χ={x1,x2,...,xN}∈RD×N,其中 x i ∈ R D × 1 , i = 1 , . . . , N x_i\in R^{D\times1},i=1,...,N xi∈RD×1,i=1,...,N,即有 N N N个样本,每个样本都是维度为 D D D的列向量。算法输出为 Y = { y 1 , y 2 , . . . , y N } ∈ R d × N Y=\{y_1, y_2,...,y_N\}\in R^{d\times N} Y={y1,y2,...,yN}∈Rd×N,其中 d < D d
首先看高维空间。LLE算法第一步是求出原始输入空间的每个样本与其邻域的线性关系,即 arg min W ∑ i = 1 N ∥ x i − ∑ j = 1 k w j i x j i ∥ 2 \mathop{\arg\min}_{W} \sum_{i=1}^N \| x_i-\sum_{j=1}^k w_{ji}x_{ji} \|^2 argminWi=1∑N∥xi−j=1∑kwjixji∥2 s . t . ∑ j = 1 k w j i = 1 s.t. \ \sum_{j=1}^k w_{ji}=1 s.t. j=1∑kwji=1记 Φ ( W ) = ∑ i = 1 N ∥ x i − ∑ j = 1 k w j i x j i ∥ 2 = ∑ i = 1 N ∥ ∑ j = 1 k ( x i − x j i ) w j i ∥ 2 = ∑ i = 1 N ∥ ( X i − N i ) W i ∥ 2 = ∑ i = 1 N W i T ( X i − N i ) T ( X i − N i ) W i \begin{aligned} \Phi(W) &= \sum_{i=1}^N \| x_i-\sum_{j=1}^k w_{ji}x_{ji} \|^2 \\ &= \sum_{i=1}^N \| \sum_{j=1}^k (x_i-x_{ji}) w_{ji} \|^2 \\ &= \sum_{i=1}^N \| (X_i-N_i)W_i \|^2 \\ &= \sum_{i=1}^N W_i ^T(X_i-N_i)^T(X_i-N_i)W_i \end{aligned} Φ(W)=i=1∑N∥xi−j=1∑kwjixji∥2=i=1∑N∥j=1∑k(xi−xji)wji∥2=i=1∑N∥(Xi−Ni)Wi∥2=i=1∑NWiT(Xi−Ni)T(Xi−Ni)Wi s . t . W i T 1 k = 1 s.t. \ \ W_i^T \boldsymbol {1}_k=1 s.t. WiT1k=1 其中 X i , N i ∈ R D × k , W i ∈ R k × 1 X_i,N_i\in R^{D\times k},W_i\in R^{k\times 1} Xi,Ni∈RD×k,Wi∈Rk×1。记 S = ( X i − N i ) T ( X i − N i ) ∈ R k × k S=(X_i-N_i)^T(X_i-N_i) \in R^{k\times k} S=(Xi−Ni)T(Xi−Ni)∈Rk×k,则上述优化目标变成了: Φ ( W ) = ∑ i = 1 N W i T S W i \Phi(W)= \sum_{i=1}^N W_i ^TSW_i Φ(W)=i=1∑NWiTSWi s . t . W i T 1 k = 1 s.t. \ \ W_i^T \boldsymbol {1}_k=1 s.t. WiT1k=1 写出该优化目标的拉格朗日方程: L = W i T S W i + λ ( W i T 1 k − 1 ) L=W_i ^TSW_i + \lambda (W_i^T \boldsymbol {1}_k-1) L=WiTSWi+λ(WiT1k−1) 求 L L L对 W i W_i Wi的偏导数,并令其等于零: ∂ L ∂ W i = 2 S W i + λ 1 k = 0 \frac{\partial L}{\partial W_i} =2SW_i+\lambda \boldsymbol {1}_k=0 ∂Wi∂L=2SWi+λ1k=0 则可以求出 W i W_i Wi: W i = S i − 1 1 k 1 k T S i − 1 1 k W_i=\frac{S_i^{-1} \boldsymbol {1}_k}{\boldsymbol {1}_k ^TS_i^{-1} \boldsymbol {1}_k} Wi=1kTSi−11kSi−11k 上式中的分母 1 k T S i − 1 1 k \boldsymbol {1}_k ^TS_i^{-1} \boldsymbol {1}_k 1kTSi−11k是为了对 W i ∈ R k × 1 W_i \in R^{k \times 1} Wi∈Rk×1进行归一化,使得 W i W_i Wi各维度之和为1,所以这里可以忽略系数 λ \lambda λ,总体的权重系数 W W W矩阵为 W = { W 1 , W 2 , . . . , W N } ∈ R k × N W=\{ W_1, W_2,...,W_N \} \in R^{k \times N} W={W1,W2,...,WN}∈Rk×N。
然后看低维空间 Y = { y 1 , y 2 , . . . , y N } ∈ R d × N Y=\{y_1, y_2,...,y_N\}\in R^{d\times N} Y={y1,y2,...,yN}∈Rd×N, Y Y Y的每一列都是一个样本,样本长度为 d d d,共 N N N个样本,因为低维空间要保证局部线性与原始输入空间相同,所以可以表示为: arg min Y ∑ i = 1 N ∥ y i − ∑ j = 1 k w j i y j i ∥ 2 \mathop{\arg\min}_{Y} \sum_{i=1}^N \| y_i-\sum_{j=1}^k w_{ji}y_{ji} \|^2 argminYi=1∑N∥yi−j=1∑kwjiyji∥2 s . t . ∑ i = 1 N y i = 0 ∑ i = 1 N y i y i T = N I d × d \begin{aligned} s.t. \ & \sum_{i=1}^N y_i=0 \\ & \sum_{i=1}^N y_i y_i^T=NI_{d \times d} \end{aligned} s.t. i=1∑Nyi=0i=1∑NyiyiT=NId×d 这里有两个约束条件,第一个是说 Y Y Y被中心化,所有的样本在同一个维度上的数值之和为0,第二个约束条件指的是 Y Y Y中的低维样本 y i y_i yi都是单位向量。现建立稀疏矩阵 W ′ = { w i j ′ } ∈ R N × N W'=\{ w'_{ij} \} \in R^{N \times N} W′={wij′}∈RN×N,且 w i j ′ = { w i j , x j ∈ k N N ( x i ) 0 , o t h e r w i s e w'_{ij}=\left\{ \begin{aligned} &w_{ij}, \ \ \ x_j \in kNN(x_i)\\ &0, \ \ \ \ \ \ \ otherwise\\ \end{aligned} \right. wij′={wij, xj∈kNN(xi)0, otherwise 因此, ∑ j = 1 N w j i ′ y j i = ∑ j = 1 k w j i y j i = Y W i ′ \sum_{j=1}^N w'_{ji}y_{ji} = \sum_{j=1}^k w_{ji}y_{ji} = YW'_i j=1∑Nwji′yji=j=1∑kwjiyji=YWi′ 上式中, Y ∈ R d × N Y \in R^{d \times N} Y∈Rd×N每一列代表一个样本, W i ′ ∈ R N × 1 W '_i\in R^{N \times 1} Wi′∈RN×1为矩阵 W ′ W' W′的列向量,得到的结果刚好是 y i ∈ R d × 1 y_i \in R^{d \times 1} yi∈Rd×1。记 Φ ( Y ) = ∑ i = 1 N ∥ y i − ∑ j = 1 k w j i y j i ∥ 2 = ∑ i = 1 N ∥ Y ( I i − W i ′ ) ∥ 2 = ∑ i = 1 N [ Y ( I i − W i ′ ) ( I i − W i ′ ) T Y T ] = t r ( Y ( I − W ′ ) ( I − W ′ ) T Y T ) \begin{aligned} \Phi(Y) &= \sum_{i=1}^N \| y_i-\sum_{j=1}^k w_{ji}y_{ji} \|^2 \\ &= \sum_{i=1}^N \| Y(I_i-W'_i) \|^2 \\ &= \sum_{i=1}^N [Y(I_i-W'_i)(I_i-W'_i)^TY ^T] \\ &= tr(Y(I-W')(I-W')^TY ^T) \end{aligned} Φ(Y)=i=1∑N∥yi−j=1∑kwjiyji∥2=i=1∑N∥Y(Ii−Wi′)∥2=i=1∑N[Y(Ii−Wi′)(Ii−Wi′)TYT]=tr(Y(I−W′)(I−W′)TYT) 这里用到了矩阵的一个技巧,假定 A = [ a 1 , a 2 , , . . . , a n ] A=[a_1, a_2, ,...,a_n] A=[a1,a2,,...,an], a n ∈ R d × 1 a_n \in R^{d \times 1} an∈Rd×1为列向量,则 ∑ i = 1 N a i 2 = ∑ i = 1 N a i T a i = t r ( A A T ) \sum_{i=1}^N a_i^2 = \sum_{i=1}^N a_i^T a_i = tr(AA^T) ∑i=1Nai2=∑i=1NaiTai=tr(AAT)(结果最后为一个数值,即 ∑ i = 1 d ∑ j = 1 N A i j 2 \sum_{i=1}^d \sum_{j=1}^N A_{ij}^2 ∑i=1d∑j=1NAij2),可以使用三元数组举一个toy problem,篇幅所限就不列举出来了。所以同样, ∑ i = 1 N y i T y i = t r ( Y Y T ) \sum_{i=1}^N y_i^T y_i = tr(YY^T) ∑i=1NyiTyi=tr(YYT)。令 M = ( I i − W i ′ ) ( I i − W i ′ ) T ∈ R N × N M=(I_i-W'_i)(I_i-W'_i)^T\in R^{N \times N} M=(Ii−Wi′)(Ii−Wi′)T∈RN×N,则优化问题可写为: m i n Φ ( Y ) = t r ( Y M Y T ) min \ \ \Phi(Y)=tr(YMY^T) min Φ(Y)=tr(YMYT) s . t . t r ( Y Y T − N I d × d ) = 0 s.t. \ \ tr(YY^T-NI_{d \times d})=0 s.t. tr(YYT−NId×d)=0 写出拉格朗日方程: L = t r [ Y M Y T + λ ( Y Y T − N I d × d ) ] L=tr[YMY^T+\lambda(YY^T-NI_{d \times d})] L=tr[YMYT+λ(YYT−NId×d)] 对 Y Y Y求导并令其等于零,则可以得到 M Y T + 2 λ Y T = 0 MY_T+2 \lambda Y_T=0 MYT+2λYT=0 M Y T = λ ′ Y T MY_T=\lambda' Y_T MYT=λ′YT 最后,要得到降维后的 d d d维数据集,只需要取矩阵 M M M最小的 d d d个特征值对应的特征向量组成的矩阵 Y ∈ R d × N Y \in R^{d\times N} Y∈Rd×N,由于 M M M最小的特征值一般为 0 0 0,所以去掉最小的特征值,选择 M M M的第 2 2 2到第 d + 1 d+1 d+1特征值对应的特征向量。这里分析一下为什么 M M M最小的特征值为 0 0 0:矩阵 W ′ W' W′的每一列的和都为 1 1 1,那么有 W ′ T 1 N = 1 N W'^T \boldsymbol {1}_N = \boldsymbol {1}_N W′T1N=1N,这里的 1 N \boldsymbol {1}_N 1N指的是长度为 N N N的全 1 1 1列向量,所以有 ( W ′ T − I ) 1 N = 0 (W'^T-I) \boldsymbol {1}_N=0 (W′T−I)1N=0,即 W ′ T − I W'^T-I W′T−I为奇异矩阵,所以 M M M也是奇异矩阵,也就是说 0 0 0是 M M M的一个特征值。
然后把代码贴出来,详细代码见我的GitHub,首先是求距离矩阵然后计算K近邻的索引:
def cal_pairwise_dist(data):
expand_ = data[:, np.newaxis, :]
repeat1 = np.repeat(expand_, data.shape[0], axis=1)
repeat2 = np.swapaxes(repeat1, 0, 1)
D = np.linalg.norm(repeat1 - repeat2, ord=2, axis=-1, keepdims=True).squeeze(-1)
return D
def get_n_neighbors(data, n_neighbors=10):
dist = cal_pairwise_dist(data)
dist[dist < 0] = 0
n = dist.shape[0]
N = np.zeros((n, n_neighbors))
for i in range(n):
# np.argsort 列表从小到大的索引
index_ = np.argsort(dist[i])[1:n_neighbors+1]
N[i] = N[i] + index_
return N.astype(np.int32) # [n_features, n_neighbors]
然后是LLE算法的核心:
def lle(data, n_dims=2, n_neighbors=10):
N = get_n_neighbors(data, n_neighbors) # k近邻索引
n, D = data.shape # n_samples, n_features
# prevent Si to small
if n_neighbors > D:
tol = 1e-3
else:
tol = 0
# calculate W
W = np.zeros((n_neighbors, n))
I = np.ones((n_neighbors, 1))
for i in range(n): # data[i] => [1, n_features]
Xi = np.tile(data[i], (n_neighbors, 1)).T # [n_features, n_neighbors]
# N[i] => [1, n_neighbors]
Ni = data[N[i]].T # [n_features, n_neighbors]
Si = np.dot((Xi-Ni).T, (Xi-Ni)) # [n_neighbors, n_neighbors]
Si = Si + np.eye(n_neighbors)*tol*np.trace(Si)
Si_inv = np.linalg.pinv(Si)
wi = (np.dot(Si_inv, I)) / (np.dot(np.dot(I.T, Si_inv), I)[0,0])
W[:, i] = wi[:,0]
W_y = np.zeros((n, n))
for i in range(n):
index = N[i]
for j in range(n_neighbors):
W_y[index[j],i] = W[j,i]
I_y = np.eye(n)
M = np.dot((I_y - W_y), (I_y - W_y).T)
eig_val, eig_vector = np.linalg.eig(M)
index_ = np.argsort(np.abs(eig_val))[1:n_dims+1]
Y = eig_vector[:, index_]
return Y