我是这样一步步理解--主题模型(Topic Model)、LDA(案例代码)
文章目录
- 1. LDA模型是什么
- 1.1 5个分布的理解
- 1.2 3个基础模型的理解
- 1.3 LDA模型
- 2. 怎么确定LDA的topic个数?
- 3. 如何用主题模型解决推荐系统中的冷启动问题?
- 4. 参考文献
- 5. 代码实现
1. LDA模型是什么
LDA可以分为以下5个步骤:
- 一个函数:gamma函数。
- 四个分布:二项分布、多项分布、beta分布、Dirichlet分布。
- 一个概念和一个理念:共轭先验和贝叶斯框架。
- 两个模型:pLSA、LDA。
- 一个采样:Gibbs采样
关于LDA有两种含义,一种是线性判别分析(Linear Discriminant Analysis),一种是概率主题模型:隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),本文讲后者。
按照wiki上的介绍,LDA由Blei, David M.、Ng, Andrew Y.、Jordan于2003年提出,是一种主题模型,它可以将文档集 中每篇文档的主题以概率分布的形式给出,从而通过分析一些文档抽取出它们的主题(分布)出来后,便可以根据主题(分布)进行主题聚类或文本分类。同时,它是一种典型的词袋模型,即一篇文档是由一组词构成,词与词之间没有先后顺序的关系。此外,一篇文档可以包含多个主题,文档中每一个词都由其中的一个主题生成。
人类是怎么生成文档的呢?首先先列出几个主题,然后以一定的概率选择主题,以一定的概率选择这个主题包含的词汇,最终组合成一篇文章。如下图所示(其中不同颜色的词语分别对应上图中不同主题下的词)。
那么LDA就是跟这个反过来:根据给定的一篇文档,反推其主题分布。
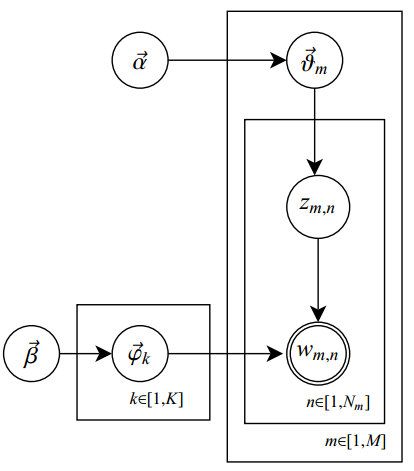
在LDA模型中,一篇文档生成的方式如下:
- 从狄利克雷分布 α \alpha α 中取样生成文档 i 的主题分布 θ i \theta_i θi。
- 从主题的多项式分布 θ i \theta_i θi 中取样生成文档i第 j 个词的主题 z i , j z_{i,j} zi,j。
- 从狄利克雷分布 β \beta β 中取样生成主题 z i , j z_{i,j} zi,j 对应的词语分布 ϕ z i , j \phi_{z_{i,j}} ϕzi,j。
- 从词语的多项式分布 ϕ z i , j \phi_{z_{i,j}} ϕzi,j 中采样最终生成词语 w i , j w_{i,j} wi,j。
其中,类似Beta分布是二项式分布的共轭先验概率分布,而狄利克雷分布(Dirichlet分布)是多项式分布的共轭先验概率分布。此外,LDA的图模型结构如下图所示(类似贝叶斯网络结构):
1.1 5个分布的理解
先解释一下以上出现的概念。
-
二项分布(Binomial distribution)
二项分布是从伯努利分布推进的。伯努利分布,又称两点分布或0-1分布,是一个离散型的随机分布,其中的随机变量只有两类取值,非正即负{+,-}。而二项分布即重复n次的伯努利试验,记为 X ∼ b ( n , p ) X\sim_{}b(n,p) X∼b(n,p)。简言之,只做一次实验,是伯努利分布,重复做了n次,是二项分布。
-
多项分布
是二项分布扩展到多维的情况。多项分布是指单次试验中的随机变量的取值不再是0-1的,而是有多种离散值可能(1,2,3…,k)。比如投掷6个面的骰子实验,N次实验结果服从K=6的多项分布。其中:
∑ i = 1 k p i = 1 , p i > 0 \sum_{i=1}^{k}p_i=1,p_i>0 i=1∑kpi=1,pi>0
-
共轭先验分布
在贝叶斯统计中,如果后验分布与先验分布属于同类,则先验分布与后验分布被称为共轭分布,而先验分布被称为似然函数的共轭先验。
-
Beta分布
二项分布的共轭先验分布。给定参数 α > 0 \alpha>0 α>0 和 β > 0 \beta>0 β>0,取值范围为[0,1]的随机变量 x 的概率密度函数:
f ( x ; α , β ) = 1 B ( α , β ) x α − 1 ( 1 − x ) β − 1 f(x;\alpha,\beta)=\frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1} f(x;α,β)=B(α,β)1xα−1(1−x)β−1
其中:
1 B ( α , β ) = Γ ( α + β ) Γ ( α ) Γ ( β ) \frac{1}{B(\alpha,\beta)}=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} B(α,β)1=Γ(α)Γ(β)Γ(α+β)
Γ ( z ) = ∫ 0 ∞ t z − 1 e − t d t \Gamma(z)=\int_{0}^{\infty}t^{z-1}e^{-t}dt Γ(z)=∫0∞tz−1e−tdt
注:这便是所谓的gamma函数,下文会具体阐述。
-
狄利克雷分布
是beta分布在高维度上的推广。Dirichlet分布的的密度函数形式跟beta分布的密度函数如出一辙:
f ( x 1 , x 2 , . . . , x k ; α 1 , α 2 , . . . , α k ) = 1 B ( α ) ∏ i = 1 k x i α i − 1 f(x_1,x_2,...,x_k;\alpha_1,\alpha_2,...,\alpha_k)=\frac{1}{B(\alpha)}\prod_{i=1}^{k}x_i^{\alpha^i-1} f(x1,x2,...,xk;α1,α2,...,αk)=B(α)1i=1∏kxiαi−1
其中
B ( α ) = ∏ i = 1 k Γ ( α i ) Γ ( ∑ i = 1 k α i ) , ∑ x i = 1 B(\alpha)=\frac{\prod_{i=1}^{k}\Gamma(\alpha^i)}{\Gamma(\sum_{i=1}^{k}\alpha^i)},\sum_{}x_i=1 B(α)=Γ(∑i=1kαi)∏i=1kΓ(αi),∑xi=1
至此,我们可以看到二项分布和多项分布很相似,Beta分布和Dirichlet 分布很相似。
如果想要深究其原理可以参考:通俗理解LDA主题模型,也可以先往下走,最后在回过头来看详细的公式,就更能明白了。
总之,可以得到以下几点信息。
-
beta分布是二项式分布的共轭先验概率分布:对于非负实数 α \alpha α 和 β \beta β ,我们有如下关系:
B e t a ( p ∣ α , β ) + C o u n t ( m 1 , m 2 ) = B e t a ( p ∣ α + m 1 , β + m 2 ) Beta(p|\alpha,\beta)+Count(m_1,m_2)=Beta(p|\alpha+m_1,\beta+m_2) Beta(p∣α,β)+Count(m1,m2)=Beta(p∣α+m1,β+m2)
其中 ( m 1 , m 2 ) (m_1,m_2) (m1,m2) 对应的是二项分布 B ( m 1 + m 2 , p ) B(m_1+m_2,p) B(m1+m2,p) 的记数。针对于这种观测到的数据符合二项分布,参数的先验分布和后验分布都是Beta分布的情况,就是Beta-Binomial 共轭。”
-
狄利克雷分布(Dirichlet分布)是多项式分布的共轭先验概率分布,一般表达式如下:
D i r ( p ⃗ ∣ α ⃗ ) + M u l t C o u n t ( m ⃗ ) = D i r ( p ∣ α ⃗ + m ⃗ ) Dir(\vec{p}|\vec\alpha)+MultCount(\vec{m})=Dir(p|\vec{\alpha}+\vec{m}) Dir(p∣α)+MultCount(m)=Dir(p∣α+m)
针对于这种观测到的数据符合多项分布,参数的先验分布和后验分布都是Dirichlet 分布的情况,就是 Dirichlet-Multinomial 共轭。 ”
-
贝叶斯派思考问题的固定模式:
先验分布 π ( θ ) \pi(\theta) π(θ)+ 样本信息 X X X = 后验分布 π ( θ ∣ x ) \pi(\theta|x) π(θ∣x)。
1.2 3个基础模型的理解
在讲LDA模型之前,再循序渐进理解基础模型:Unigram model、mixture of unigrams model,以及跟LDA最为接近的pLSA模型。为了方便描述,首先定义一些变量:
- w w w 表示词, V V V 表示所有单词的个数(固定值)。
- z z z 表示主题, k k k 是主题的个数(预先给定,固定值)。
- D = ( W 1 , . . . , W M ) D=(W_1,...,W_M) D=(W1,...,WM) 表示语料库,其中的M是语料库中的文档数(固定值)。
- W = ( w 1 , w 2 , . . . , w N ) W=(w_1,w_2,...,w_N) W=(w1,w2,...,wN) 表示文档,其中的N表示一个文档中的词数(随机变量)。
-
Unigram model
对于文档 W = ( w 1 , w 2 , . . . , w N ) W=(w_1,w_2,...,w_N) W=(w1,w2,...,wN),用 p ( w n ) p(w_n) p(wn) 表示词 w n w_n wn 的先验概率,生成文档w的概率为:
p ( W ) = ∏ n = 1 N p ( w n ) p(W)=\prod_{n=1}^{N}p(w_n) p(W)=n=1∏Np(wn)
-
Mixture of unigrams model
该模型的生成过程是:给某个文档先选择一个主题z,再根据该主题生成文档,该文档中的所有词都来自一个主题。假设主题有 z 1 , . . . , z n z_1,...,z_n z1,...,zn,生成文档w的概率为:
p ( W ) = p ( z 1 ) ∏ n = 1 N p ( w n ∣ z 1 ) + . . . + p ( z k ) ∏ n = 1 N p ( w n ∣ z k ) = ∑ z p ( z ) ∏ n = 1 N p ( w n ∣ z ) p(W)=p(z_1)\prod_{n=1}^{N}p(w_n|z_1)+...+p(z_k)\prod_{n=1}^{N}p(w_n|z_k)=\sum_{z}p(z)\prod_{n=1}^{N}p(w_n|z) p(W)=p(z1)n=1∏Np(wn∣z1)+...+p(zk)n=1∏Np(wn∣zk)=z∑p(z)n=1∏Np(wn∣z)
-
PLSA模型
理解了pLSA模型后,到LDA模型也就一步之遥——给pLSA加上贝叶斯框架,便是LDA。
在上面的Mixture of unigrams model中,我们假定一篇文档只有一个主题生成,可实际中,一篇文章往往有多个主题,只是这多个主题各自在文档中出现的概率大小不一样。比如介绍一个国家的文档中,往往会分别从教育、经济、交通等多个主题进行介绍。那么在pLSA中,文档是怎样被生成的呢?
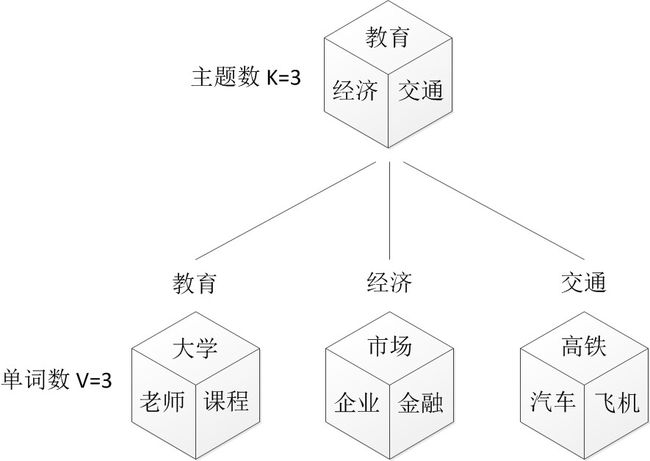
假定你一共有K个可选的主题,有V个可选的词,咱们来玩一个扔骰子的游戏。
**一、**假设你每写一篇文档会制作一颗K面的“文档-主题”骰子(扔此骰子能得到K个主题中的任意一个),和K个V面的“主题-词项” 骰子(每个骰子对应一个主题,K个骰子对应之前的K个主题,且骰子的每一面对应要选择的词项,V个面对应着V个可选的词)。
比如可令K=3,即制作1个含有3个主题的“文档-主题”骰子,这3个主题可以是:教育、经济、交通。然后令V = 3,制作3个有着3面的“主题-词项”骰子,其中,教育主题骰子的3个面上的词可以是:大学、老师、课程,经济主题骰子的3个面上的词可以是:市场、企业、金融,交通主题骰子的3个面上的词可以是:高铁、汽车、飞机。
**二、**每写一个词,先扔该“文档-主题”骰子选择主题,得到主题的结果后,使用和主题结果对应的那颗“主题-词项”骰子,扔该骰子选择要写的词。
先扔“文档-主题”的骰子,假设(以一定的概率)得到的主题是教育,所以下一步便是扔教育主题筛子,(以一定的概率)得到教育主题筛子对应的某个词:大学。
上面这个投骰子产生词的过程简化下便是:“先以一定的概率选取主题,再以一定的概率选取词”。
**三、**最后,你不停的重复扔“文档-主题”骰子和”主题-词项“骰子,重复N次(产生N个词),完成一篇文档,重复这产生一篇文档的方法M次,则完成M篇文档。
上述过程抽象出来即是PLSA的文档生成模型。在这个过程中,我们并未关注词和词之间的出现顺序,所以pLSA是一种词袋方法。生成文档的整个过程便是选定文档生成主题,确定主题生成词。
反过来,既然文档已经产生,那么如何根据已经产生好的文档反推其主题呢?这个利用看到的文档推断其隐藏的主题(分布)的过程(其实也就是产生文档的逆过程),便是主题建模的目的:自动地发现文档集中的主题(分布)。
文档d和词w是我们得到的样本,可观测得到,所以对于任意一篇文档,其 P ( w j ∣ d i ) P(w_j|d_i) P(wj∣di) 是已知的。从而可以根据大量已知的文档-词项信息 P ( w j ∣ d i ) P(w_j|d_i) P(wj∣di),训练出文档-主题 P ( z k ∣ d i ) P(z_k|d_i) P(zk∣di) 和主题-词项 P ( w j ∣ z k ) P(w_j|z_k) P(wj∣zk),如下公式所示:
P ( w j ∣ d i ) = ∑ k = 1 K P ( w j ∣ z k ) P ( z k ∣ d i ) P(w_j|d_i)=\sum_{k=1}^{K}P(w_j|z_k)P(z_k|d_i) P(wj∣di)=k=1∑KP(wj∣zk)P(zk∣di)
故得到文档中每个词的生成概率为:
P ( d i , w j ) = P ( d i ) P ( w j ∣ d i ) = P ( d i ) ∑ k = 1 K P ( w j ∣ z k ) P ( z k ∣ d i ) P(d_i,w_j)=P(d_i)P(w_j|d_i)=P(d_i)\sum_{k=1}^{K}P(w_j|z_k)P(z_k|d_i) P(di,wj)=P(di)P(wj∣di)=P(di)k=1∑KP(wj∣zk)P(zk∣di)
由于 P ( d i ) P(d_i) P(di) 可事先计算求出,而 P ( w j ∣ z k ) P(w_j|z_k)^{} P(wj∣zk) 和 P ( z k ∣ d i ) P(z_k|d_i) P(zk∣di) 未知,所以 θ = ( P ( w j ∣ z k ) , P ( z k ∣ d i ) ) \theta=(P(w_j|z_k),P(z_k|d_i)) θ=(P(wj∣zk),P(zk∣di)) 就是我们要估计的参数(值),通俗点说,就是要最大化这个θ。
用什么方法进行估计呢,常用的参数估计方法有极大似然估计MLE、最大后验证估计MAP、贝叶斯估计等等。因为该待估计的参数中含有隐变量z,所以我们可以考虑EM算法。详细的EM算法可以参考之前写过的 EM算法 章节。
1.3 LDA模型
事实上,理解了pLSA模型,也就差不多快理解了LDA模型,因为LDA就是在pLSA的基础上加层贝叶斯框架,即LDA就是pLSA的贝叶斯版本(正因为LDA被贝叶斯化了,所以才需要考虑历史先验知识,才加的两个先验参数)。
下面,咱们对比下本文开头所述的LDA模型中一篇文档生成的方式是怎样的:
- 按照先验概率 P ( d i ) P(d_i) P(di) 选择一篇文档 d i d_i di。
- 从狄利克雷分布(即Dirichlet分布) α \alpha α 中取样生成文档 d i d_i di 的主题分布 θ i \theta_i θi,换言之,主题分布 θ i \theta_i θi 由超参数为 α \alpha α 的Dirichlet分布生成。
- 从主题的多项式分布 θ i \theta_i θi 中取样生成文档 d i d_i di 第 j 个词的主题 z i , j z_{i,j} zi,j。
- 从狄利克雷分布(即Dirichlet分布) β \beta β 中取样生成主题 z i , j z_{i,j} zi,j 对应的词语分布 ϕ z i , j \phi_{z_{i,j}} ϕzi,j,换言之,词语分布 ϕ z i , j \phi_{z_{i,j}} ϕzi,j 由参数为 β \beta β 的Dirichlet分布生成。
- 从词语的多项式分布 ϕ z i , j \phi_{z_{i,j}} ϕzi,j 中采样最终生成词语 w i , j w_{i,j} wi,j。
LDA中,选主题和选词依然都是两个随机的过程,依然可能是先从主题分布{教育:0.5,经济:0.3,交通:0.2}中抽取出主题:教育,然后再从该主题对应的词分布{大学:0.5,老师:0.3,课程:0.2}中抽取出词:大学。
那PLSA跟LDA的区别在于什么地方呢?区别就在于:
PLSA中,主题分布和词分布是唯一确定的,能明确的指出主题分布可能就是{教育:0.5,经济:0.3,交通:0.2},词分布可能就是{大学:0.5,老师:0.3,课程:0.2}。
但在LDA中,主题分布和词分布不再唯一确定不变,即无法确切给出。例如主题分布可能是{教育:0.5,经济:0.3,交通:0.2},也可能是{教育:0.6,经济:0.2,交通:0.2},到底是哪个我们不再确定(即不知道),因为它是随机的可变化的。但再怎么变化,也依然服从一定的分布,即主题分布跟词分布由Dirichlet先验随机确定。正因为LDA是PLSA的贝叶斯版本,所以主题分布跟词分布本身由先验知识随机给定。
换言之,LDA在pLSA的基础上给这两参数 ( P ( z k ∣ d i ) 、 P ( w j ∣ z k ) ) (P(z_k|d_i)、P(w_j|z_k)) (P(zk∣di)、P(wj∣zk)) 加了两个先验分布的参数(贝叶斯化):一个主题分布的先验分布Dirichlet分布 α \alpha α,和一个词语分布的先验分布Dirichlet分布 β \beta β。
综上,LDA真的只是pLSA的贝叶斯版本,文档生成后,两者都要根据文档去推断其主题分布和词语分布(即两者本质都是为了估计给定文档生成主题,给定主题生成词语的概率),只是用的参数推断方法不同,在pLSA中用极大似然估计的思想去推断两未知的固定参数,而LDA则把这两参数弄成随机变量,且加入dirichlet先验。
所以,pLSA跟LDA的本质区别就在于它们去估计未知参数所采用的思想不同,前者用的是频率派思想,后者用的是贝叶斯派思想。
LDA参数估计:Gibbs采样,详见文末的参考文献。
2. 怎么确定LDA的topic个数?
- 基于经验 主观判断、不断调试、操作性强、最为常用。
- 基于困惑度(主要是比较两个模型之间的好坏)。
- 使用Log-边际似然函数的方法,这种方法也挺常用的。
- 非参数方法:Teh提出的基于狄利克雷过程的HDP法。
- 基于主题之间的相似度:计算主题向量之间的余弦距离,KL距离等。
3. 如何用主题模型解决推荐系统中的冷启动问题?
推荐系统中的冷启动问题是指在没有大量用户数据的情况下如何给用户进行个性化推荐,目的是最优化点击率、转化率或用户 体验(用户停留时间、留存率等)。冷启动问题一般分为用户冷启动、物品冷启动和系统冷启动三大类。
- 用户冷启动是指对一个之前没有行为或行为极少的新用户进行推荐;
- 物品冷启动是指为一个新上市的商品或电影(这时没有与之相关的 评分或用户行为数据)寻找到具有潜在兴趣的用户;
- 系统冷启动是指如何为一个 新开发的网站设计个性化推荐系统。
解决冷启动问题的方法一般是基于内容的推荐。以Hulu的场景为例,对于用 户冷启动来说,我们希望根据用户的注册信息(如:年龄、性别、爱好等)、搜 索关键词或者合法站外得到的其他信息(例如用户使用Facebook账号登录,并得 到授权,可以得到Facebook中的朋友关系和评论内容)来推测用户的兴趣主题。 得到用户的兴趣主题之后,我们就可以找到与该用户兴趣主题相同的其他用户, 通过他们的历史行为来预测用户感兴趣的电影是什么。
同样地,对于物品冷启动问题,我们也可以根据电影的导演、演员、类别、关键词等信息推测该电影所属于的主题,然后基于主题向量找到相似的电影,并将新电影推荐给以往喜欢看这 些相似电影的用户。可以使用主题模型(pLSA、LDA等)得到用户和电影的主题。
以用户为例,我们将每个用户看作主题模型中的一篇文档,用户对应的特征 作为文档中的单词,这样每个用户可以表示成一袋子特征的形式。通过主题模型 学习之后,经常共同出现的特征将会对应同一个主题,同时每个用户也会相应地 得到一个主题分布。每个电影的主题分布也可以用类似的方法得到。
**那么如何解决系统冷启动问题呢?**首先可以得到每个用户和电影对应的主题向量,除此之外,还需要知道用户主题和电影主题之间的偏好程度,也就是哪些主题的用户可能喜欢哪些主题的电影。当系统中没有任何数据时,我们需要一些先验知识来指定,并且由于主题的数目通常比较小,随着系统的上线,收集到少量的数据之后我们就可以对主题之间的偏好程度得到一个比较准确的估计。
4. 参考文献
通俗理解LDA主题模型
5. 代码实现
LDA模型应用:一眼看穿希拉里的邮件
【机器学习通俗易懂系列文章】
![]()
作者:@mantchs
GitHub:https://github.com/NLP-LOVE/ML-NLP
欢迎大家加入讨论!共同完善此项目!群号:【541954936】
我的博客即将同步至腾讯云+社区,邀请大家一同入驻:https://cloud.tencent.com/developer/support-plan?invite_code=2uu2jp8vgf8k0