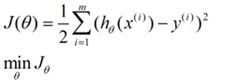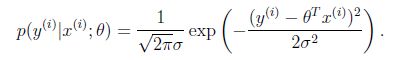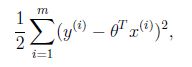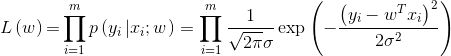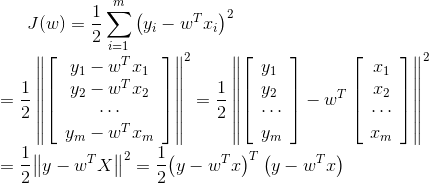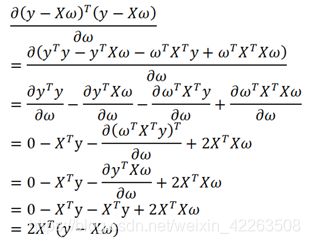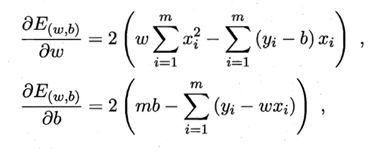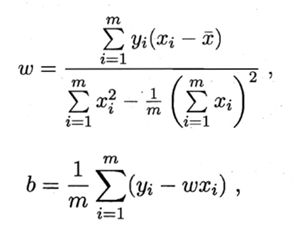线性回归原理及python实现
- 概念
线性回归(Linear Regression)是一种通过属性的线性组合来进行预测的线性模型,其目的是找到一条直线或者一个平面或者更高维的超平面,使得预测值与真实值之间的误差最小化。 - 特点
优点:结果具有很好的可解释性(w直观表达了各属性在预测中的重要性),计算熵不复杂。
缺点:对非线性数据拟合不好
适用数据类型:数值型和标称型数据
3.函数模型:
模型表达:
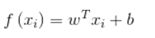
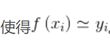
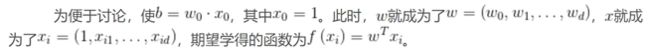
预测值和真实值之间存在误差:即:
4.损失函数:
为什么要用这个损失函数?
一般来讲,误差满足平均值为0的高斯分布,也就是正态分布。那么x和y的条件概率也就是
这样就估计了一条样本的结果概率,然而我们期待的是模型能够在全部样本上预测最准,也就是概率积最大。注意这里的概率积是概率密度函数积,连续函数的概率密度函数与离散值的概率函数不同。这个概率积成为最大似然估计。我们希望在最大似然估计得到最大值时确定θ。那么需要对最大似然估计公式求导,求导结果既是:
这就解释了为何误差函数要使用平方和。
当然推导过程中也做了一些假定,但这个假定符合客观规律。
5.求解损失函数:(下式中ω=θ)
对数似然函数:
得到目标函数:
为什么要让目标函数越小越好:似然函数表示样本成为真实的概率,似然函数越大越好,也就是目标函数 ![]() 越小越好。
越小越好。
目标函数是凸函数,只要找到一阶导数为0的位置,就找到了最优解。
因此求偏导:
矩阵求导请查看处,注意矩阵多项式求导,与我们直观上不一样,所以我在此贴出来,可以研究下:(https://blog.csdn.net/weixin_42263508/article/details/89882658)
令偏导等于0:
得到:
情况一:可逆,唯一解。令公式上式为零可得最优解为:
学得的线性回归模型为:
情况二:不可逆,可能有多个解。选择哪一个解作为输出,将有学习算法的偏好决定,常见的做法是增加扰动。
上述是矩阵解法.
下面是直接求导解:
Python实践算法:
import numpy as np
def linar_loss(X, y, w, b):
num_train = X.shape[0]
num_feature = X.shape[1]
#模型公式
y_hat = np.dot(X, w) + b
#损失函数
loss = np.sum((y_hat-y)**2)/num_train
#参数的偏导
dw = np.dot(X.T,(y_hat - y)) /num_train
db = np.sum((y_hat- y ))/num_train
return y_hat, loss, dw, db
def initialize(dims):
w = np.zeros((dims,1))
b = 0
return w,b
def linar_train(x,y,learning_rate,epochs):
w,b = initialize(x.shape[1])
print("w = %s" % w)
print("b = %s" % b)
loss_list=[]
for i in range(1,epochs):
#计算当前预测值,损失和参数偏导
y_hat, loss, dw, db = linar_loss(x, y, w, b)
loss_list.append(loss)
#基于梯度下降的参数更新过程
w += -learning_rate * dw
b += -learning_rate * db
#打印迭代次数和损失
if i % 10000 ==0:
print("epoch %d loss %f" %(i,loss))
#保存参数
params = {
'w' : w,
'b' : b
}
#保存梯度
grads = {
'dw':dw,
'db':db
}
return loss_list, loss, params, grads
from sklearn.datasets import load_diabetes
from sklearn.utils import shuffle
diabetes = load_diabetes()
data = diabetes.data
target = diabetes.target
#打乱数据
x, y =shuffle(data, target,random_state=13)
x = x.astype(np.float32)
#训练集与测试集的简单划分
# print("x.shape[1]:%s"%x.shape[1])
# print("x.shape[0]:%s"%len(x))
offset = int(x.shape[0]*0.9)#offset=397
print("offset:%s"% offset)
x_train,y_train = x[:offset],y[:offset]
# print("x_train :%s"%x_train)
x_test,y_test = x[offset:],y[offset:]
y_train=y_train.reshape(-1,1)
y_test = y_test.reshape(-1,1)
# print("y_train :%s" %y_train)
loss_list,loss,params,grads = linar_train(x_train,y_train,0.001,100000)
print(params)
def predict(X,params):
w = params['w']
b = params['b']
y_pred = np.dot(X,w) + b
return y_pred
y_pred = predict(x_test,params)
y_pred[:5]
import matplotlib.pyplot as plt
f = x_test.dot(params['w']) + params['b']
plt.scatter(range(x_test.shape[0]), y_test)
plt.plot(f, color = 'darkorange')
plt.xlabel('X')
plt.ylabel('y')
plt.show()