python实现关联规则分析Apriori算法

代码写了好久了，今天搬上来。
Apriori算法介绍：


Apriori其实是为了降低搜索空间以及提高搜索速度而设计的一种算法，本文采用python实现，彻底理解“频繁项集的所有非空子集一定是频繁的”这句话，并实现连接步、剪枝步、规则生成、提升度计算等。
本节代码参考了《机器学习实战》第十一章中的代码，也参考了R语言的arules包，该包没有实现一对多的规则，因此，在以上基础上进行了改进，包括实现剪枝步，规则生成（一对一，一对多，多对一，多对多），增加提升度Lift评估。

整体代码实现过程如下：

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
from numpy import *

def loadDataSet():
    return [['a', 'c', 'e'], ['b', 'd'], ['b', 'c'], ['a', 'b', 'c', 'd'], ['a', 'b'], ['b', 'c'], ['a', 'b'],
            ['a', 'b', 'c', 'e'], ['a', 'b', 'c'], ['a', 'c', 'e']]


def createC1(dataSet):
    C1 = []
    for transaction in dataSet:
        for item in transaction:
            if not [item] in C1:
                C1.append([item])
    C1.sort()
    # 映射为frozenset唯一性的，可使用其构造字典
    return list(map(frozenset, C1))      


# 从候选K项集到频繁K项集（支持度计算）
def scanD(D, Ck, minSupport):
    ssCnt = {}
    for tid in D:
        for can in Ck:
            if can.issubset(tid):
                if not can in ssCnt:
                    ssCnt[can] = 1
                else:
                    ssCnt[can] += 1
    numItems = float(len(D))
    retList = []
    supportData = {}
    for key in ssCnt:
        support = ssCnt[key] / numItems
        if support >= minSupport:
            retList.insert(0, key)
            supportData[key] = support  
    return retList, supportData


def calSupport(D, Ck, min_support):
    dict_sup = {}
    for i in D:
        for j in Ck:
            if j.issubset(i):
                if not j in dict_sup:
                    dict_sup[j] = 1
                else:
                    dict_sup[j] += 1
    sumCount = float(len(D))
    supportData = {}
    relist = []
    for i in dict_sup:
        temp_sup = dict_sup[i] / sumCount
        if temp_sup >= min_support:
            relist.append(i)
            supportData[i] = temp_sup  # 此处可设置返回全部的支持度数据（或者频繁项集的支持度数据）
    return relist, supportData


# 改进剪枝算法
def aprioriGen(Lk, k):  # 创建候选K项集 ##LK为频繁K项集
    retList = []
    lenLk = len(Lk)
    for i in range(lenLk):
        for j in range(i + 1, lenLk):
            L1 = list(Lk[i])[:k - 2]
            L2 = list(Lk[j])[:k - 2]
            L1.sort()
            L2.sort()
            if L1 == L2:  # 前k-1项相等，则可相乘，这样可防止重复项出现
                #  进行剪枝（a1为k项集中的一个元素，b为它的所有k-1项子集）
                a = Lk[i] | Lk[j]  # a为frozenset()集合
                a1 = list(a)
                b = []
                # 遍历取出每一个元素，转换为set，依次从a1中剔除该元素，并加入到b中
                for q in range(len(a1)):
                    t = [a1[q]]
                    tt = frozenset(set(a1) - set(t))
                    b.append(tt)
                t = 0
                for w in b:
                    # 当b（即所有k-1项子集）都是Lk（频繁的）的子集，则保留，否则删除。
                    if w in Lk:
                        t += 1
                if t == len(b):
                    retList.append(b[0] | b[1])
    return retList


def apriori(dataSet, minSupport=0.2):
    C1 = createC1(dataSet)
    D = list(map(set, dataSet))  # 使用list()转换为列表
    L1, supportData = calSupport(D, C1, minSupport)
    L = [L1]  # 加列表框，使得1项集为一个单独元素
    k = 2
    while (len(L[k - 2]) > 0):
        Ck = aprioriGen(L[k - 2], k)
        Lk, supK = scanD(D, Ck, minSupport)  # scan DB to get Lk
        supportData.update(supK)
        L.append(Lk)  # L最后一个值为空集
        k += 1
    del L[-1]  # 删除最后一个空集
    return L, supportData  # L为频繁项集，为一个列表，1，2，3项集分别为一个元素。


# 生成集合的所有子集
def getSubset(fromList, toList):
    for i in range(len(fromList)):
        t = [fromList[i]]
        tt = frozenset(set(fromList) - set(t))
        if not tt in toList:
            toList.append(tt)
            tt = list(tt)
            if len(tt) > 1:
                getSubset(tt, toList)


def calcConf(freqSet, H, supportData, ruleList, minConf=0.7):
    for conseq in H:
        conf = supportData[freqSet] / supportData[freqSet - conseq]  # 计算置信度
        # 提升度lift计算lift = p(a & b) / p(a)*p(b)
        lift = supportData[freqSet] / (supportData[conseq] * supportData[freqSet - conseq])

        if conf >= minConf and lift > 1:
            print(freqSet - conseq, '-->', conseq, '支持度', round(supportData[freqSet - conseq], 2), '置信度：', conf,
                  'lift值为：', round(lift, 2))
            ruleList.append((freqSet - conseq, conseq, conf))

# 生成规则
def gen_rule(L, supportData, minConf=0.7):
    bigRuleList = []
    for i in range(1, len(L)):  # 从二项集开始计算
        for freqSet in L[i]:  # freqSet为所有的k项集
            # 求该三项集的所有非空子集，1项集，2项集，直到k-1项集，用H1表示，为list类型,里面为frozenset类型，
            H1 = list(freqSet)
            all_subset = []
            getSubset(H1, all_subset)  # 生成所有的子集
            calcConf(freqSet, all_subset, supportData, bigRuleList, minConf)
    return bigRuleList


if __name__ == '__main__':
    dataSet = loadDataSet()
    L, supportData = apriori(dataSet, minSupport=0.2)
    rule = gen_rule(L, supportData, minConf=0.7)

结果如下所示（更完善）：

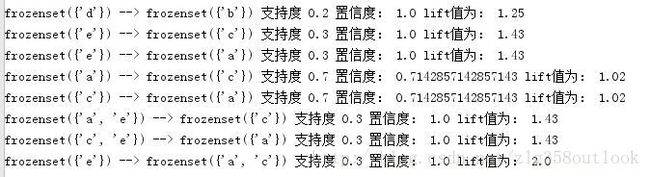
R语言运行结果（存在不足）：

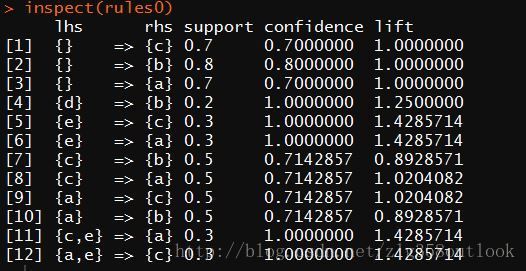
R语言实现中，去掉第1-3条涉及空集的规则，删除Lift小于1的情况（第7条和第10条），剩余7条规则。与上图本文实现相比较，少了“一对多”的情况，也就是少了“e—–a，c”这条规则。

大功告成，代码实现比较好懂，功能都实现了，较R语言结果展现有了明显的改进（自动删除涉及空集的规则，自定义筛选Lift>1），但是看起来比较乱，有时间重新封装下，先写到这里，睡觉。