Android 淘气三千传之——Android搜索中前缀匹配的一点理解
目录
1、前言
2、相关知识点
3、内容
4、问题
5、总结
6、参考文章 & 推荐阅读
1、前言
咳咳,当我们在浏览器、在手机的电话联系人界面等等地方,输入一段字符串之后,就可以匹配出相应前缀的结果出来(如使用 AutoCompleteTextView 输入字段就会有相应的结果匹配),在存储本地数据的时候,由于数据后期可能会变多,所以需要进行缓存或者添加数据库索引,(量级肯定不能和服务端相比),由于是需要通过前缀关键字来搜索得到结果,所以具有一定的特殊性,所以对缓存和索引的知识点简单地梳理了一下。
2、相关知识点
我们的目的都是为了提高数据检索效率,既然是前缀,符合这个特征的,映入脑海的首先是 Trie 了,同时,我们需要考虑的还有空间、时间,涉及到的一共有以下知识点:
- Trie
- Hash Tree
- 索引
- 三叉树 (Ternary Search Trie)
- 番外:fm-index
3、内容
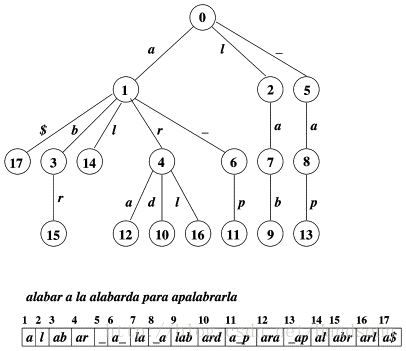
1) Trie (前缀树、字典树)
注:图片来自 http://www.sciencedirect.com/science/article/pii/S1570866703000662
Trie 作为比较常见的数据结构,包含了以下特点:
- 根为空,不包含字符
- 从根到某一个节点连接起来是一个字符串
- 插入时间为 O(n) n 是字符串长度
我们可以尝试写一个简单的Trie,构造的 Trie 如下:
public class TrieNode {
public int path; // 多少个字符串有经过这个节点
public int end; // 多少个字符串以这个节点结束
public TrieNode[] map;
public TrieNode() {
path = 0;
end = 0;
map = new TrieNode[26];
}
}
public class Trie {
private TrieNode root;
private List result;
private StringBuilder stringBuilder = new StringBuilder();
public Trie() {
root = new TrieNode();
}
public void insert(String word) {
if (word == null) {
return;
}
char[] chs = word.toCharArray();
TrieNode node = root;
int index = 0;
for (int i = 0; i < chs.length; i++) {
index = chs[i] - 'a';
if (node.map[index] == null) {
node.map[index] = new TrieNode();
}
node = node.map[index];
node.path++;
}
node.end++;
}
public List searchStr(String word) {
if (word == null) {
return null;
}
char[] chs = word.toCharArray();
TrieNode node = root;
int index = 0;
for (int i = 0; i < chs.length; i++) {
index = chs[i] - 'a';
stringBuilder.append(chs[i]);
if (node.map[index] == null)
return null;
node = node.map[index];
}
if (node.path != 0) {
result = new ArrayList<>();
if (node.end != 0)
result.add(stringBuilder.toString());
getStr(node);
return result;
} else {
return null;
}
}
//通过 DFS 对树进行搜索
private void getStr(TrieNode node) {
for (int i = 0; i < 26; i++) {
if (node.map[i] != null) {
stringBuilder.append((char) (i + 'a'));
if (node.map[i].end != 0)
result.add(stringBuilder.toString());
getStr(node.map[i]);
}
}
}
} 然后跑下下面的代码,测试一下效果:
String[] s = {"abc", "abcd", "ab","ijk","bcd","ijkkk","ijkkkkkk"};
Trie trie = new Trie();
for (int i = 0; i < s.length; i++) {
trie.insert(s[i]);
}
List<String> re = trie.searchStr("ijkk");
for (String i : re) {
System.out.println(i);
}结果如下:
这边缓存是用英文字符串做key,所以只需要 26 个字母,如果是中文缓存呢,由于中文较多,个人认为可以考虑转换成拼音,然后做为key(假如是中文作为关键字,那么会使用很多的空间),接着按照英文的来构造Trie 即可。
同时从我们写的代码可以看出来,插入时间是 O(strLen),并且每个节点都有26个指针,即使该指针没有值,这样占用的空间就会比较大。
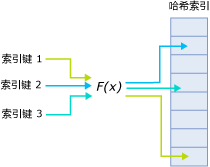
2)Hash Tree(哈希树、哈希表、散列表)
Hash的概念大概如下:把一个大范围的数字 哈希(转化)成一个小范围的数字,这个小的范围对应着数组的下标,使用哈希函数向数组插入数据后,这个数组就成为哈希表,在最坏情况下,哈希表查找一个元素时间和链表时间相同,达到了 O(n),实际应用中查找性能是极好的,所以在一些合理的假设下,在哈希表中查找一个元素的平均时间是 O(1)。同时,哈希表还在另一个类似的领域得到广泛应用,这就是高级计算机语言的编译器,他们通常用哈希表保留符号表(符号表记录了咱们在程序中声明的所有变量和函数名,以及它们在内存中的地址)。
a、说到哈希,一般提到最多的是哈希碰撞,
b、那么,说到哈希树,需要提及到一个理论,就是 质数分辨定理 ,如下:
简单地证明下(写在纸上的截图):
一言蔽之:n个互不相同的质数,小于这些 质数乘积个数 的两个整数 k1 和 k2,它们的余数不可能总相等。
那么,通过此定理,可以构造一棵减少hash碰撞的树。也就是说,如果从第一层子节点开始(根为空节点),第一层有2个节点,第一层的每个节点有3个子节点,第二层的每个节点有5个子节点,以此类推,2、3、5、7 。。。,构造了一个质数的 Hash Tree,比如到第10个质数字,总数已经有 2*3*5…*29 个了,小于这个乘积的数字,可以通过取余来得到位置:先从第一层开始,对 2 取余,如果该节点已经有 value 了,那么探测第二层,对3取余,以此类推,最多到第十层。(注意:每次拿来取余的 除数 都是 Pi,也就是不同的层不是对同一个质数来取余,可以看下定理表达)
这个定理是一种处理哈希碰撞的方式,处理冲突的还有 链地址法、开放地址法 等,在开放地址法中进行线性探测、二次探测或者再哈希时,都要求数组容量选一个质数。这些方式都是为了更好的处理哈希碰撞,提高哈希表性能,比如 java 里面的 hash 函数也是为了更好的 hash
另外,在 HashMap 中,JDK 1.7及之前通过 数组+链表 来处理数据,1.8 之后通过 数组+链表+红黑树 来处理,一般在搜索时,插入删除次数多的情况下用红黑树来取代 AVL 。
3)索引
当我们要提高查询速度节省时间时,就会使用到索引,索引有哈希索引,B树索引等等
在内存里,可以通过指针或者引用来链接到下一个节点,在磁盘中,通过文件中块的编号来进行链接。通常,定位到一页信息并将其从磁盘里读出的时间要比读出信息的时间要长的多。(磁盘的转动类似老式留声机,具体可以网上参考)
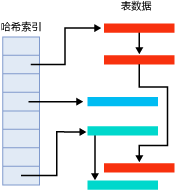
a、哈希索引
上面提到了hash,这里顺便梳理下哈希索引
外部哈希化的关键部分是一个哈希表,它包含了块成员,指向外部存储器中的块。哈希表又是叫做索引。
在外部哈希中,重要的是块不要填满,所有关键字映射为同一个值的记录都定位到相同块,为找到特定关键字的一个记录,搜索算法哈希化关键字,用哈希值作为哈希表的下标,得到某个下标中的块号,然后读取这个块。这个过程是有效的,因为定位一个特定的数据项,只需要访问一次块,缺点是相当多的磁盘空间被浪费了。
推荐阅读:https://msdn.microsoft.com/zh-cn/library/dn133190.aspx
b、B树索引
B树有 B- 和 B+ 树(B-树和B树是同一种树),
上图中的树是一棵 2-3-4 树(B-树的一个特例),可以看到,
- 非叶子结点 D 的子节点数L总是比节点的数据项D多1,即 L = D + 1;
- 同时子节点的数据项大小按照一定关键字排序,每个子节点数据项都在一个范围内,如 {1,2,5,6} 都是小于 7 ,中间的,{9,12} 都是 大于7小于16,右边的 {18,21} 都大于16,这里的比较都是开区间
- 并且叶子节点都在同一层上;
- 树是平衡的,即使插入一列升序或者降序的数据都能保持平衡,平衡能力取决于插入新节点的方式
- 在查找的时候,从根开始,向下查找,如果在对应层找不到,通过 对比目标 Key的大小,先找出 Key 在该层哪个范围,如 Key 为 8,可以看到,8在 {7,16}之间,然后再沿着这个范围中的引用往下查找,知道找到或者节点为空。
在对大文件进行操作时,运行时间主要考虑两个成分,一个是磁盘的存取次数,另一个是CPU(计算)时间,在一个典型的B树应用中,所要处理的数据量非常大,以至于所有数据无法一次装入主存。B树算法将所需页面从磁盘复制到主存,然后将修改过的页面写回磁盘。在任何时刻,B树算法都只需要在主存中保持一定数量的页面,因此,主存的大小并不限制被处理的B树的大小。
B+树:关于 B- 树的理解可以先结合 2-3-4 树来理解。 在其它的一些B-树里,如变身版本B+树,只有叶节点保存数据,非叶节点只保存关键字和块的号码。这会使得操作更快,因为每一块可以保存跟多块的号码,这样的高阶树层数更少,访问速度也会提高。
索引也还有其它如位图索引等等。。。如此篇介绍:http://www.cnblogs.com/LBSer/p/3322630.html 此处就不展开
4)三叉树
Trie 作为很消耗内存的数据结构,有一种比较好的改进:三叉树
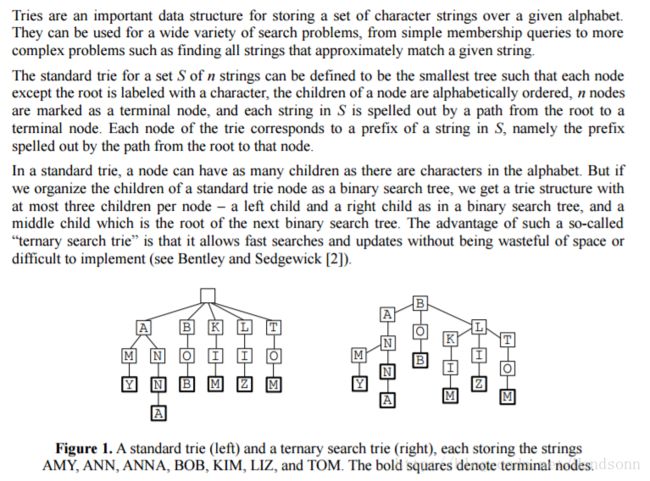
先通过一段文字来了解下三叉树(翻译不好,直接贴图):
从中提取出几个点:
1、标准的 Trie 它的每个节点都有相同数量的子节点,(如上面写的 Trie的代码),因此对空间的使用也会比较大
2、(这篇文章)提出的三叉树用了 “Treap”来维持三叉树的平衡,这样就可以避免极端退化成链表
3、三叉树的 时间是 O(k+logN) ( Treap 树在增删查改中是期望的logN,并且 Trie 是 O(k))
4、相对当前较小的字符放到左边、相等的放到中间、较大的放到右边,强调随机插入,而不是按照字典序来插入字符
更多三叉树的介绍可以参考以下链接:
https://arxiv.org/abs/1606.04042 写的非常棒,同时里面给出了伪代码的流程
参考这篇文章的描述,尝试写一个简单的三叉树,如下:
public class TstNode {
TstNode left;
TstNode right;
TstNode middle;
HashMap map;
public int path; // 多少个字符串有经过这个节点
public int end; // 多少个字符串以这个节点结束
char c;
public TstNode() {
path = 0;
end = 0;
}
public TstNode(char c) {
path = 0;
end = 0;
this.c = c;
map = new HashMap<>();
}
} public class TernarySearchTrie {
private TstNode root;
private List result;
public TernarySearchTrie() {
root = new TstNode();
}
public void insert(String word) {
if (word == null)
return;
char[] chs = word.toCharArray();
TstNode node = root;
int index = 0;
int i = 0;
while (true) {
index = chs[i] - node.c;
if (index == 0) {
node.path++;
i++;
if (i == chs.length) {
// 通过用 大于0 并且 自增的 end 作为key 存储结果
node.end++;
node.map.put(node.end,word);
return;
}
if (node.middle == null)
node.middle = new TstNode(chs[i]);
node = node.middle;
} else if (index < 0) {
if (node.left == null)
node.left = new TstNode(chs[i]);
node = node.left;
} else {
if (node.right == null)
node.right = new TstNode(chs[i]);
node = node.right;
}
}
}
public List search(String word) {
result = new ArrayList<>();
if (word == null)
return result;
TstNode node = root;
char[] chs = word.toCharArray();
int index = 0;
int i = 0;
while (true) {
if (node == null)
return result;
index = chs[i] - node.c;
if (index == 0) {
i++;
if (i == chs.length) {
if(node.end != 0)
result.add(node.map.get(node.end));
if (node.left != null)
getStr(node.left);
if (node.middle != null)
getStr(node.middle);
if (node.right != null)
getStr(node.right);
return result;
}
node = node.middle;
} else if (index < 0) {
node = node.left;
} else {
node = node.right;
}
}
}
//通过 DFS 对树进行搜索
private void getStr(TstNode node) {
if (node != null) {
if (node.end != 0) {
result.add(node.map.get(node.end));
}
if (node.left != null)
getStr(node.left);
if (node.middle != null)
getStr(node.middle);
if (node.right != null)
getStr(node.right);
}
}
} 然后运行下以下代码:
TernarySearchTrie myTST = new TernarySearchTrie();
String[] s = {"j", "jk", "jkl", "jkkk", "jkkkkk","jkkkmlp","jkkabcdefg"};
for (int i = 0; i < s.length; i++)
myTST.insert(s[i]);
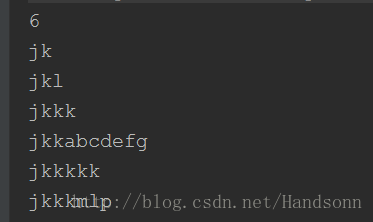
List list = myTST.search("jk");
if (list != null) {
System.out.println(list.size());
for (String m : list)
System.out.println(m);
} 结果如下:
相比 Trie,三叉树更好的节省了内存空间
5)番外:fm-index
毫无疑问,这是一个番外篇章,当索引越来越大的时候,就会占用一定的内存空间,并且索引的不断调整也会影响性能,所以对于索引,可以进行压缩,fm-index 基于一个数据转换算法 Burrows-Wheeler transform (简称BWT),转换过程比较简单,可以参考这里:https://en.wikipedia.org/wiki/Burrows%E2%80%93Wheeler_transform
这里小小地提及一下,感兴趣可以参考其它文章
![]()
4、问题:”我来了 “
a、哈希 和 Trie 哪个比较好呢?
从时间上来说:
插入和查询 一般 Trie 是 O(strLen),strLen是字符串长度,而 Hash 是 冲突的探测时间 + 计算 Hash 的常量时间,理想的Hash是O(1)的时间
从空间上来说:
Trie是一种以空间换时间的数据结构。
首先,以上构造的Trie处理的是都是关于字符串的,那么就要求了对使用的场景有一定限制,那么如果是其它场景呢,比如浮点数,那么你这棵树可能就很长了,这个时候对空间要求也会非常大,并且会有更多无用空间浪费。因此,Trie对key的要求属于是比较严格的。从使用场景来说:
Trie此类树最有用的是它的字典性质,即:在Trie中,对任意一个节点,该节点的所有子树都以该节点的 value 为前缀,这个性质是 hash 所不具备的。
可以参考 维基百科的描述:
上面这段文字分析了 Trie 和 hashtable 的利弊,比较好懂,
关于 Trie 和 HashTable 的比较 更多可以参考这篇文章 http://loup-vaillant.fr/projects/string-interning/benchmark 该文作者用纯 c 语言 写了 Trie 以及 HashTable,并且和 c++ 自带的 unordered_map 一起进行比较,一个比较重要的点是 :c++ 自带的 unordered_map 速度慢是由于每次生成一个新的字符串时间消耗导致,而不是由于hash时间。
也就是说,在特定条件下 Trie 更优
b、为什么使用索引要使用B树呢?
首先,这个索引存储在磁盘,当然,如果是内存中,也需要备份一份到磁盘,也就是外部存储。而外部存储技术细节的实现和操作系统、语言、硬件等密切相关。
磁盘驱动器访问数据有两个点:
1)磁盘驱动比主存要慢得多(磁道排列、数据旋转等)
2)一次需要访问很多记录
当读写头到达正确的位置后开始读写过程,驱动器可以很快的把大量数据转移到主存,因此,磁盘上的数据读写块的时间与块的容量关系不大,那么,块越大,读写一条记录的效率就越高。在磁盘查找和插入的过程中,效率都很低,在插入有序文件中时更低,涉及到了将一些数据块放到缓冲区,然后插入,再将放到缓冲区的数据块拿回来,直到完成插入目标数据。
那么,考虑到磁盘的I/O,此时需要树形结构来提供更加高效的增删查改了,由于B-树每个节点有很多子节点,数据项更多,将一整块数据作为树的节点就十分有意义,并且结合磁盘的局部性原理以及预读机制,每个节点恰好只需要一次磁盘的I/O,数据利用率很高。同时,B树的性质使得B树层级比较少(矮胖),所以磁盘I/O的次数相对平衡二叉树和红黑树会较少。
c、哈希索引 和 B树索引 孰优孰劣呢?
这个问题回到hash和B树的优点上,hash理想情况下可以到O(1)的时间,这是十分快的,但随着数据增加,碰撞的概率就会增加,可能还需要开辟更多空间再hash来存放更多数据,并且,hash要求是一个完整的key,那么,对于模糊查询来说不能很好实现,而B树随着数据增大,层数依然可以保持很少,B树的节点可以有很多个孩子,从数个到数千个,甚至上亿的数量。
5、总结
a、以上的数据结构在本篇文中都是为了搜索缓存以及前缀匹配的优化,在Android中,常用缓存的还有LruCache 和 DiskLruCache,LruCache 利用的是 LinkedHashMap 在内存中进行缓存,而DiskLruCache 在外部存储中进行缓存,通过IO流来进行缓存,这时就涉及到了磁盘IO了
b、对于不同的数据结构,孰优孰劣需要结合特定的场景和计算机环境不,比如内存和外部存储,需要特定的词频统计或者一整个 key-value 来获取.
c、如果要从时间上来比较的话,可以通过 VisualVm 进行时间的比较
。。。不过我在使用的时候抽风了
d、对于上面写的trie和三叉树,如果要用于生产环境,还需要经过更多数据的训练,不断改进,如果需要将树写到磁盘中,那么需要用一些标记号代替指针。
6、参考文章 & 推荐阅读
https://wenku.baidu.com/view/16b2c7abd1f34693daef3e58.html
http://loup-vaillant.fr/projects/string-interning/benchmark
https://arxiv.org/abs/1606.04042
https://leetcode.com/articles/implement-trie-prefix-tree/
http://www.sciencedirect.com/science/article/pii/S1570866703000662
https://sci-hub.org.cn/extdomains/www.google.com/patents/US5528701
https://max.book118.com/html/2017/0314/95335789.shtm
https://msdn.microsoft.com/zh-cn/library/dn133190.aspx
以上便是简单的梳理,由于个人水平有限,有纰漏或者错误的,欢迎吐槽
PS:平时如果要找一些系统的总结文章,可以先去百度学术、谷歌学术等找,在谷歌学术不能免费下载,这个时候复制链接,然后去 SCI-HUB下载,具体百度输入 SCI-HUB就知道啦