机器学习的核心概念置信度和置信区间，我用这个例子把它讲明白

1 引出概念

今天，讲一个数据分析或机器学习里非常重要的概念，置信度和置信区间。为什么说置信度和置信区间非常重要？举个例子。

拿到一个电影数据集，为了挑选出喜剧类型的电影，在豆瓣上评分前10名。这看似并不困难，使用pandas几行代码差不多就能完成分析，给出一个结果。

但是，当回过头来仔细检查时，却发现，选出的10部电影，竟然有5部电影只有一个人评分，并且都是给了10分。

基于这种情况，评选出的前10名，自然不能服众，不具有很强的说服力。

我们更期望的是，一部电影被众多观影者打分，然后从这些电影中，挑选得分更高的电影。

这里就能引出：置信度和置信区间的概念。

一部电影被众多人打分，最后平均得分为8.5，那么这部电影的得分在8.2~8.8分，置信度将会很高，假设为90%；

相反，一部电影只有两个人打分，尽管最后平均分为9.5分，但是在区间：9.2~9.8分的置信度，可能就没那么高，预估为50%吧。言外之意，这个置信区间9.2~9.8被否的可能性会更大，毕竟只有50%吗。

2 理论解释

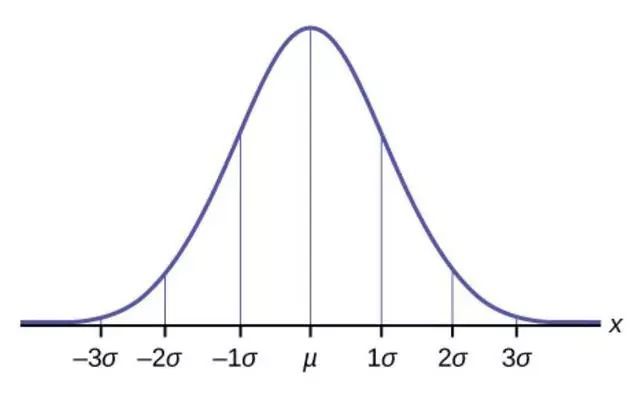
如果我们叫无数个观影者给某部电影打分，下面的图就是总体分布图，其平均得分为 μ ，标准差为 σ ：

如果我们已经得出μ 和 σ ，我们可以说约 68％ 的样本会落在红色区域：平均得分在上下两个 σ内的置信度就是95%.

假设样本无穷大，这样得到某部电影的平均得分就是总体分布得分，平均分为0.65分(满分为1分)， 标准差为0.03. 

那么这部电影的平均得分在置信区间0.62~0.68 分的置信度约为95%.

所以，为了增强结果的说服力，可以过滤掉那些被评分较少的电影，那么到底少于多少就应该被过滤掉，这里也有说法。

3 求95%置信度对应样本个数

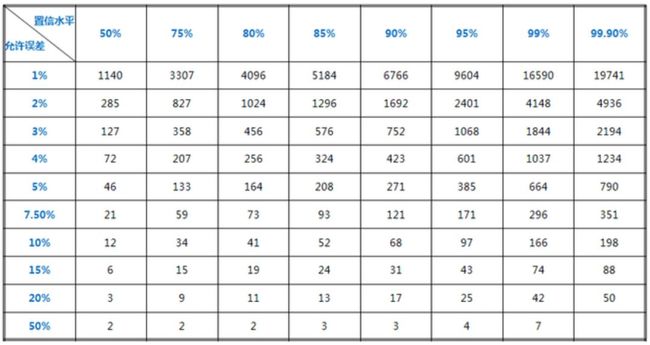
已知样本标准差，Z值，置信区间的长度，根据公式，便能计算出样本个数，具体计算公式大家自行查询，在此不列出。

表格参考如上，如果我们按照95%的置信度，允许误差为5%的话，需要的样本个数至少为385.

所以，我们的问题已经解决了，要找出至少有385次被评分的所有电影，按照喜剧的平均分依次从大到小排序，选出前10.

因为用到Z值，在此说明下Z值的求法，作为知识扩充。

4 求95%置信度对应的Z值

允许电影评分有左右各有误差，即0.05/2=0.025。此时要查尾部面积是0.025时的Z值。

查Z值表时要在表中间找到0.975。从这一行水平往左得到1.9，往上对得到0.06，把两个数加起来就是1.96。

5 求95%置信度对应的置信区间

计算置信区间：

第一步，已知样本，求样本平均值、标准差和标准误差。样本标准误差：

第二步，确定置信度（置信水平），常用的置信度是95%。 

第三步，求置信区间[a,b]上下限，Z值求法参考上面，所以容易得出：

a = 总体平均值 - Z*标准误差

b = 总体平均值 + Z*标准误差

以上这些知识点，相信大家在网上也能搜出来，但是学习最重要的是知识逻辑梳理。一个一个的知识点这就好比放到那里的一个一个的珠子，而知识的逻辑体系就好比那一根线，它把一个一个的珠子串联起来，这根线就是逻辑线。我更希望通过辛苦总结，形成这样一根串珠子的线，这才是最大的价值所在，而像珠子的知识获取手段目前从来都不匮乏。

备注：公众号菜单包含了整理了一本AI小抄，非常适合在通勤路上用学习。

往期精彩回顾




2019年公众号文章精选适合初学者入门人工智能的路线及资料下载机器学习在线手册深度学习在线手册AI基础下载（第一部分）备注：加入本站微信群或者qq群，请回复“加群”加入知识星球（4500+用户，ID：92416895），请回复“知识星球”

喜欢文章，点个在看