CS231n Spring 2019 Assignment 2—Fully-Connected Neural Nets(全连接神经网络)
Fully-Connected Neural Nets全连接神经网络
- Fully-Connected Neural Nets(全连接神经网络)
- Affine layer: foward/backward
- ReLU activation: forward/backward
- "Sandwich" layers
- Two-layer network
- Multilayer network
- Update rules
- SGD+Momentum
- RMSProp
- Adam
- Train a good model!
- 形象的动图比较
- 结果
- 链接
还是纪念一下今天早上电脑卡机按了一下强制关机就开不起来的经历吧,结果是供电线路出问题了,╮(╯▽╰)╭,该修还得修,没有电脑没法过日子啊。
Fully-Connected Neural Nets(全连接神经网络)
这一次是作业2中的Fully-Connected Neural Nets(全连接神经网络),具体要完成的就是FullyConnectedNets.ipynb,里面要完成的内容较多,我是花了3天时间才完整做完的。与之前最大不同就是:这次全是通过模块化设计,在一些网络结构里面不再把训练部分也加到函数里面,而是单独拿出来成为一块,通过前后向函数的堆叠,完成网络的设计,封装得更好了。这里还是按作业的顺序来介绍:
Affine layer: foward/backward
这里自己将它:仿射层,其实就是一个线性变换,在layers.py里面(这里面都是一些最小单位的层)编写前后向的仿射变换,虽然输入的 x x x不是二维的,但是可以经过reshape/view来变成二维的,跟之前的作业很像:
affine_forward(x, w, b) —>return out, cache
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
out = np.dot(x.reshape(x.shape[0], -1), w) + b
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
反向传播这里也写得模块化多了,传入的参数就是上游来的梯度dout和前向传播时保存的用来反向传播时用的缓存cache。代码不难:
affine_backward(dout, cache)—>return dx, dw, db
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dx = np.dot(dout, w.T)
dx = dx.reshape(x.shape)
dw = np.dot(x.reshape(x.shape[0], -1).T, dout)
db = np.sum(dout, axis=0)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
ReLU activation: forward/backward
以前我们是用
np.maximum(0, x)
来实现ReLU()函数的,现在把它封装一下当做一个层来操作,实际操作都是一样的:relu_forward(x)—>return out, cache
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
out = np.maximum(0, x)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
ReLU()函数的反向传播其实就是对矩阵中的每一个元素进行一个max gate的反向传播,就是只让正向时大于0的位置得到上游梯度,这里有一个mask的思想:
relu_backward(dout, cache)—>return dx
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dx = dout * (x > 0)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
“Sandwich” layers
顾名思义,就是像三明治一样进行各层的堆叠,将之前的Affine foward/backward layer和ReLU forward/backward activation layer进行再一次的组合封装,在layer_utils.py里面就都是简单层的复合。这里面基本上就是调用layers.py里面已经定义好的层就行,反向的时候记得按着逆序一步一步来就行:
affine_relu_forward(x, w, b)—>return out, cache
def affine_relu_forward(x, w, b):
"""
Convenience layer that perorms an affine transform followed by a ReLU
Inputs:
- x: Input to the affine layer
- w, b: Weights for the affine layer
Returns a tuple of:
- out: Output from the ReLU
- cache: Object to give to the backward pass
"""
a, fc_cache = affine_forward(x, w, b)
out, relu_cache = relu_forward(a)
cache = (fc_cache, relu_cache)
return out, cache
affine_relu_backward(dout, cache)—>return dx, dw, db
def affine_relu_backward(dout, cache):
"""
Backward pass for the affine-relu convenience layer
"""
fc_cache, relu_cache = cache
da = relu_backward(dout, relu_cache)
dx, dw, db = affine_backward(da, fc_cache)
return dx, dw, db
之后就是一个loss层,有softmax loss的,也有svm loss的,因为这在之前已经写过了,教程中在layers.py的最后也直接给出了,但还得看一遍熟悉一下传入返回参数啥的:
svm_loss(x, y)—>return loss, dx
softmax_loss(x, y)—>return loss, dx
Two-layer network
之前在作业1的时候也完成过一次两层全连接网络的编写two_layer_net.ipynb,但这次得implement modular versions。在fc_net.py完成TwoLayerNet类的编写,主要是一个参数的初始化还有loss和grad的计算,这两层网络的结构就是affine - relu - affine - softmax ,可以考虑调用前面定义好的affine_relu_forward和affine_forward和softmax_loss函数拼接而成,初始化的np.random.randn()函数返回的是指定shape的标准正太分布的numpy数组,代码如下:
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
self.params['W1'] = weight_scale * np.random.randn(input_dim, hidden_dim)
self.params['b1'] = np.zeros(hidden_dim)
self.params['W2'] = weight_scale * np.random.randn(hidden_dim, num_classes)
self.params['b2'] = np.zeros(num_classes)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
W1, b1 = self.params['W1'], self.params['b1']
W2, b2 = self.params['W2'], self.params['b2']
# affine_relu_layer
out1, cache1 = affine_relu_forward(X, W1, b1)
# affine_layer
out2, cache2 = affine_forward(out1, W2, b2)
scores = out2
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# compute loss
data_loss, dscores = softmax_loss(scores, y)
reg_loss = 0.5 * self.reg * (np.sum(W1 * W1) + np.sum(W2 * W2))
loss = data_loss + reg_loss
# compute grads
dhidden, grads['W2'], grads['b2'] = affine_backward(dscores, cache2)
grads['W2'] += self.reg * W2
dX, grads['W1'], grads['b1'] = affine_relu_backward(dhidden, cache1)
grads['W1'] += self.reg * W1
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
可以看到在TwoLayerNet类里面没有了train函数,这次也是通过在solver.py定义Solver类来进行模型的训练优化。它的类结构是这样的:
|——class Solver(object)
|—— __init__():初始化一些参数
|—— _reset():设置一些用来记录的量
|—— _step():用优化方法更新一步
|—— _save_checkpoint():保存模型用,可选
|—— check_accuracy():在提供的数据上测试准确率
|—— train():训练模型,会调用前面的_step()函数
额,这个类也不需要我们自己写,只需要会部署就好了,下面的代码里面展示了我训练的参数,在10个epoch之后在验证集上达到了51.2%的准确率,达到教程50%的要求:
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
solver = Solver(model, data, update_rule='sgd',
optim_config={'learning_rate':1e-3,},
lr_decay=0.95, num_epochs=10,
batch_size=100, print_every=100) #实例化一个对象
solver.train() # 调用Solver类方法train()进行训练
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
Multilayer network
接下来难度进一步加大,上面是定义两层的全连接神经网络,这里是要定义任意多层的神经网络,不过得益于之前的模块化设计,这里的多层网络设计起来也并不困难。跟TwoLayerNet很像,这里的FullyConnectedNet主要也是在fc_net.py中完成初始化和loss、grad的计算,其中就涉及到前向和反向传播。网络架构为{affine - [batch/layer norm] - relu - [dropout]} x (L - 1) - affine - softmax,可以考虑用affine_forward、softmax_loss和relu_forward来搭建,至于batch/layer norm和dropout可以参见下次的博文,这里可以先不写,但可以用pass来进行占位,提示下次该补全的地方。因为我是全部写好后来写的博客,我就已经写好了。结果太长,这里就不放了,具体可见fc_net.py。
Update rules
这次作业的一大重点就是优化方法的编写,主要有SGD+Momentum、RMSProp和 Adam,这一部分主要出现在
- Neural Networks Part 3: Learning and Evaluation
- Lecture 8
网上相关好文:
- 梯度下降优化算法综述
- 梯度下降优化方法总结
- 【深度学习】各种梯度下降优化方法总结
SGD+Momentum
原始的SGD(mini-batch)就是 x t + 1 = x t − α ∇ f ( x ) x_{t+1}=x_{t}-\alpha \nabla f(x) xt+1=xt−α∇f(x),非常朴素的梯度下降,但是这会有几个问题:
- 在梯度平缓的维度下降非常慢,在梯度险峻的维度容易抖动,见下图
- 容易陷入局部极小值或鞍点,在高维空间中,鞍点比局部极小值更容易出现
- 选择一个合适的学习率可能是困难的,更新方向完全依赖于当前batch计算出的梯度,因而易不稳定
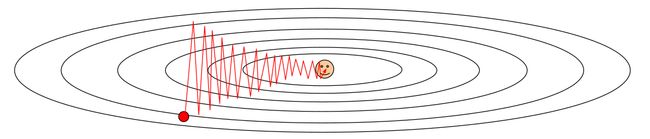
之后就有了SGD+Momentum也就是加上了动量的方法(我没有查到到底谁先提出了这个算法,好像momentum运用到网络优化中已经有些年份了,可以参读:On the momentum term in gradient descent learning algorithms和On the importance of initialization and momentum in deep learning),Momentum算法借用了物理中的动量概念,它模拟的是物体运动时的惯性,有以下几个特点:
- 更新的时候在一定程度上保留之前更新的方向,同时利用当前batch的梯度微调最终的更新方向(见下图)
- 对于在梯度点处具有相同的方向的维度,其动量项增大,对于在梯度点处改变方向的维度,其动量项减小。因此,我们可以得到更快的收敛速度,同时可以减少摇摆
具体的公式有多种形式(在代码中用了公式(2)中的):
v t + 1 = ρ v t + ∇ f ( x t ) x t + 1 = x t − α v t + 1 (1) v_{t+1}= \rho v_{t}+\nabla f(x_{t}) \\x_{t+1}=x_{t}- \alpha v_{t+1} \tag{1} vt+1=ρvt+∇f(xt)xt+1=xt−αvt+1(1)
v t + 1 = ρ v t − α ∇ f ( x t ) x t + 1 = x t + v t + 1 (2) v_{t+1}= \rho v_{t}-\alpha \nabla f(x_{t}) \\x_{t+1}=x_{t}+v_{t+1}\tag{2} vt+1=ρvt−α∇f(xt)xt+1=xt+vt+1(2)

代码:sgd_momentum(w, dw, config=None)—>return next_w, config
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
v = config['momentum'] * v - config['learning_rate'] * dw
next_w = w + v
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
RMSProp
RMSprop是一个未被发表的自适应学习率的算法,该算法由Geoff Hinton在其Coursera课堂的课程6e中提出,RMSprop其实解决了Adagrad的极速递减的学习率问题,从下图可以看出两者的不同(Adagrad会累加之前所有的梯度平方,而RMSprop仅仅是计算平方梯度的滑动平均值):
E [ g 2 ] t = 0.9 E [ g 2 ] t − 1 + 0.1 g t 2 θ t + 1 = θ t − η E [ g 2 ] t + ϵ g t E[g^2]_t = 0.9 E[g^2]_{t-1} + 0.1 g^2_t \\ \theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t} E[g2]t=0.9E[g2]t−1+0.1gt2θt+1=θt−E[g2]t+ϵηgt

代码:rmsprop(w, dw, config=None)—>return next_w, config
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
cache = config.get('cache')
cache = config['decay_rate'] * cache + (1 - config['decay_rate']) * (dw ** 2)
next_w = w + -config['learning_rate'] * dw / (np.sqrt(cache) + config['epsilon'])
config['cache'] = cache
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
Adam
自适应矩估计(Adaptive Moment Estimation,Adam)是另一种自适应学习率的算法,Adam对每一个参数都计算自适应的学习率:
- 除了像RMSprop一样存储一个滑动平均的历史平方梯度
- Adam同时还保存一个历史梯度的滑动平均值,类似于动量,可以说结合了Momentum和RMSprop的特点
完整版的adam长这样:

代码:adam(w, dw, config=None)—>return next_w, config
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
config['t'] += 1
config['m'] = config['beta1'] * config['m'] + (1 - config['beta1']) * dw
mt = config['m'] / (1 - config['beta1'] ** config['t'])
config['v'] = config['beta2'] * config['v'] + (1 - config['beta2']) * (dw ** 2)
vt = config['v'] / (1 - config['beta2'] ** config['t'])
next_w = w - config['learning_rate'] * mt / (np.sqrt(vt) + config['epsilon'])
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
Train a good model!
这里是通过FullyConnectedNet构建全连接网络模型,在cifar10上进行训练,要求是在验证集上能达到50%的准确率(现在还没有使用)BatchNormalization和Dropout,可能会低一点,你可以在我的基础上细调(包括优化方法,学习率等;我加入了一点计算训练时间的代码),我在验证集上达到了52.9%的准确率,在测试集上达到了52.8%的准确率:
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Check train and val accuracy on the first iteration, the last
# iteration, and at the end of each epoch.
# Append loss(not train or val loss) per iteration
import time
tic = time.time()
X_val= data['X_val']
y_val= data['y_val']
X_test= data['X_test']
y_test= data['y_test']
regularization_strength = 1e-2
# weight_scales = [2.5e-2, 5e-2]
# learning_rates = [1e-3, 3e-3, 1e-2]
# batch_sizes = [100]
weight_scales = [5e-2]
learning_rates = [1e-3]
batch_sizes = [200]
for ws in weight_scales:
for lr in learning_rates:
for bs in batch_sizes:
model = FullyConnectedNet([600, 500, 400, 300, 200, 100],
weight_scale=ws,
reg = regularization_strength, dtype=np.float64,
dropout=1, normalization='batchnorm')
solver = Solver(model, data,
print_every=500, num_epochs=30, batch_size=bs,
update_rule='adam',
optim_config={
'learning_rate': lr,
},
lr_decay=0.95) # decay learning rate when epoch increase 1
print('weight_scales = %f, learning_rates = %f, batch_sizes = %f' % (ws, lr, bs))
solver.train()
y_val_pred = np.argmax(model.loss(X_val), axis=1)
val_acc = (y_val_pred == y_val).mean()
print('val_acc = %f' % (val_acc))
print('=========================================================================')
if val_acc > best_val:
best_val = val_acc
best_model = model
toc = time.time()
total_seconds = int(toc - tic)
hours = total_seconds // 3600
minutes = (total_seconds - hours * 3600) // 60
seconds = total_seconds - hours * 3600 - minutes * 60
print('Training took %d hours %d minutes %d seconds' % (hours, minutes, seconds))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
形象的动图比较
结果
具体可见FullyConnectedNets.ipynb
链接
前后面的作业博文请见:
- 上一篇的博文:two_layer_net/features
- 下一篇的博文:Batch Normalization批量归一化

