深度强化学习cs294 Lecture6: Actor-Critic Algorithms

复习一下上节课的策略梯度算法。主要就是对目标函数的定义以及梯度的计算。还有一些减小方差的方法以及Importance Sampling的方法。

1. Improving the policy gradient with a critic

在公式里从当前开始得到的反馈值之和$Q_{i,t}^{\pi }$有一个更好的估计方式：

这表示当前状态$s_t$采取了动作$a_t$之后后面会得到的所有反馈和的期望值。对应的有一个在当前状态$s_t$的期望值，就是对Q进行在$a_t$上求期望：

在policy gradient方法中使用一个常数b作为一个baseline来减小梯度的方差。这里的b就是对Q值的一个平均，那么就可以使用V来替代，而原本的$Q_{i,t}^{\pi }$也可以用新的期望值$Q^{\pi }(s_t,a_t)$替代。这样就得到了两个期望值的差值，我们把这个值叫做advantage函数。

使用了advantage函数的梯度求导，如果advantage函数估计得越准确，那么梯度的方差就会越小。而原来的使用一个序列的反馈值之和减去b的方式，方差更大。不过是一个无偏估计。

因此使用新的期望函数来计算梯度，但是需要计算三个不同的值$Q,V,A$比较麻烦，可以看一下它们之间的关系。因为$Q^{\pi }(s_t,a_t)$对应的是一个固定的状态动作对$(s_t,a_t)$，因此有一步的反馈值r已经固定不变了，也就是$Q^{\pi }(s_t,a_t)=r(s_t,a_t)+E_{s_{t+1}\sim p(s_{t+1}|s_t)}[V^{\pi }(s_{t+1})]$，如果采用采样近似期望的形式可以写为$Q^{\pi }(s_t,a_t)\approx r(s_t,a_t)+V^{\pi }(s_{t+1})$。这样我们在计算梯度的过程中只需要计算一个期望函数$V^{\pi }(s_t)$即可，这个一般也使用神经网络来进行逼近。

2. The policy evaluation problem

从期望值V的定义可以看出，强化学习的目标函数其实就是这个值关于初始状态$s_1$的期望值。也就是说计算$V^{\pi }$就是对当前的策略进行一个评价，评价当前策略是好是坏。我们有两种MC方法能够估算出对应的V值，但是第二种对序列进行平均的方式不太好实现，因此一般使用第一个简单的形式：

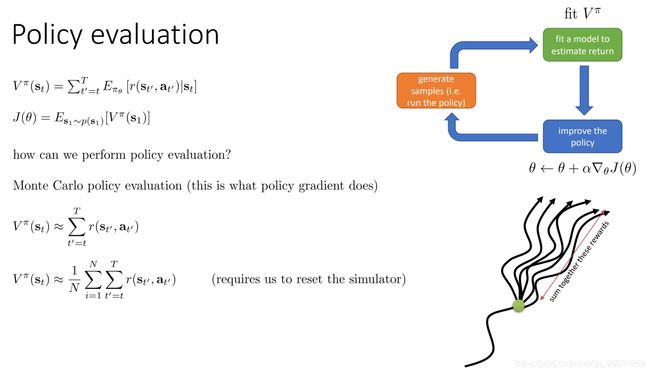
因此我们就有了目标label，下面用监督学习的方式来对这个V值做一个拟合即可，拟合的目标函数是均方误差，这样训练就能得到一个能够拟合出状态值函数的神经网络：

不过实际上我们可以做得更精确一些。因为这里直接使用了一个序列样本的反馈和作为目标值，实际上方差会很大。可以利用一个近似的方式来减小方差。$y_{i,t}={\sum }_{t^{\prime }=t}^T{E}_{{\pi }_{\theta }}[r(s_{t^{\prime }},a_{t^{\prime }})|s_{i,t}]\approx r(s_{i,t},a_{i,t})+V^{\pi }(s_t)\approx r(s_i,a_i)+V_{\varphi }^{\pi }(s_{i,t+1})$。这个方法叫做自举。其中使用了下一个状态的估计值来计算前一个时间状态的估计值。这样做能够减小方差，因为计算的结果不是一个采样而是一个期望。但是会引入一些误差，因为当前的估计函数并不是真实的V值。

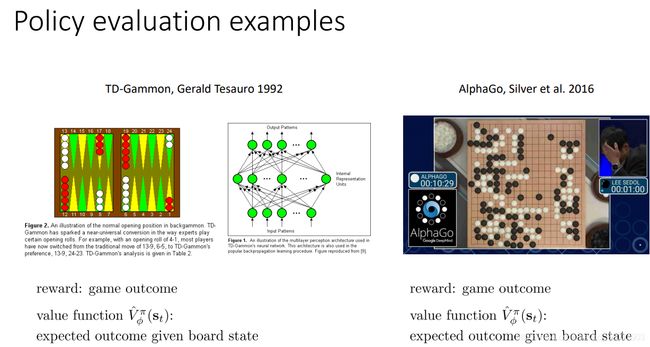
有很多成功的例子都使用了这个方法，比如TD-gammon和Alphago。

于是我们就得到了一个新的形式的actor-critic算法：

3. Discount factors

上面的actor-critic算法里第一步还需要采样一整个序列。想要变成每次只采样一个状态即可，还需要先引入Discount factors的设定。

因为值函数V的定义是当前状态以后所有反馈值的和，在有限步长的任务中没有问题，但是如果是一个无限步长的任务，那么这个值有可能是无限大的。因此需要引入一个折损系数$\gamma$，它的意义在于让离当前状态比较近的反馈值更重要，而离得比较远的可能不那么看重。

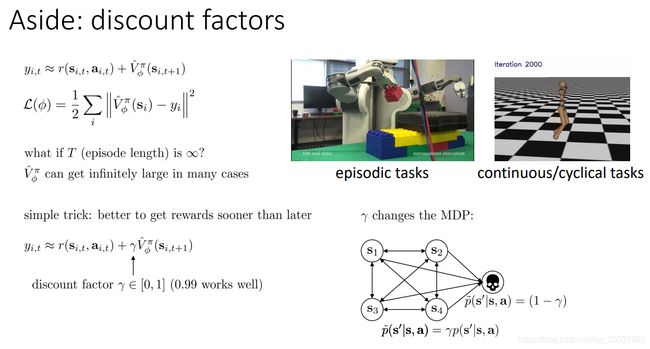
这个系数虽然看似加在了反馈值上面，但实际上会对MDP的概率做一个改变。它相当于增加了一个额外的状态，每个状态转移都有$1-\gamma$的概率转移到这个死亡状态里。这个状态代表着任务失败或意外结束。

不过对于目标函数梯度的计算，加入discount factors的写法可以有两种。

第一种写法是直接从当前时间t开始加系数$\gamma$，而第二种写法是从最开始$t=1$的时候就开始加系数。然后再通过利用因果率去掉$t^{\prime }$之前的反馈值。这样最终两种写法的系数还是有一些差别。

一般情况下两种方式有两种不同的解释和应用场景。第二种写法是对应着带有死亡状态的MDP形式。系数从第一步就开始加入，这就意味着这种写法更在意从头开始的动作，对于往后的动作给的关注更少。

而第一种写法是从时刻t开始加系数，也就是说它会一直在意从当前时刻开始的动作。这种形式一般用在一直连续运动的场景里。

第一种写法实际上不是一个正确的加了discount factor后的写法。它相当于是对平均反馈值加了一个系数来减小方差，它去除掉那些距离太远的反馈值的影响，因为可能太远了已经没有了意义。当然这样会是平均反馈的有偏估计。具体的数学部分在ppt下方的论文里。

第一种写法实际中更常用，也就是作为减小方差的方式。而第二种写法能够向我们解释在经典的场景里discount factor的意义。

加入了discount factors之后的actor-critic算法可以采用对每个状态进行采用的形式，这样就有了online形式的算法。

4. The actor-critic algorithm

在实际实现actor-critic算法的时候可以选择两种结构。一种是让策略函数与值函数分别训练。这样做可能比较简单而且稳定，但是这样就不能共享一些提取特征的网络层。第二种是两种函数共享一部分网络，这样就能够共享前面提取特征的部分。

实际上如果实现一个online形式的算法，最好的做法并不是对每一个状态都做一次更新，而是得到足够多的样本里作为一个batch来更新。因为这样能够减小更新的方差。而实现这样的方式也有两种，一种是同步的一种是异步的。

异步强化学习算法在本课后面会有详细的讨论。

比较一下和原来的policy gradient相比，actor-critic算法在更新的时候有更小的方差，但是它使用的值函数是有偏的。而policy gradient算法虽然是无偏的，但是带来的方差太大了。我们可以将它们两个算法做一个组合，利用它们两种方法的优点：

能够得到一个没有偏差而且方差较小的版本。

State-dependent baselines

之前用到作为baseline的函数一直都是状态值函数V，实际上状态动作值函数Q也能够作为baseline。只不过这样做实际上得到的不是一个advantage函数，在期望上得到一个期望为0的函数。因为减小了这部分的值，就能够减小对应部分的方差。

但是期望为0直接带入得不到目标函数的梯度值，因此计算梯度值的时候还需要把$Q_{\varphi }^{\pi }(s_t,a_t)$以期望的形式加回来，这样目标函数梯度值的期望与原来保持一致。为什么要多做这一步，因为$Q_{\varphi }^{\pi }(s_t,a_t)$的期望在一些情况下有闭式解，因此比较好得到。比如Q是动作a的二次函数而策略是高斯分布的时候（我懂了吗？我没有懂）。

目前我们有两种得到advantage函数的形式，一种是完全自举的，有更低的方差，但是有比较高的偏差。第二种是蒙特卡洛采样减去估计值的，这样做没有偏差，但是方差比较大。因此我们需要想办法把这两种结合起来：

实际上第一种写法是一个一步return的写法，如果把一步变为n步，而n趋近于无穷的时候就等同于MC采样，而n>1的其它情况能够利用这两种写法的优势，得到方差较小偏差也较小的结果。具体可以看sutton的书或者n步自举。

还有个在n步自举之上更加泛化的形式，那就是资格迹。同样可以看sutton的书或者资格迹。这里讲得比较简略，大致就是将不同的n步结果的advantage函数再加权求和一次：

同样的最后是为了减小方差。

回顾一下本节课的内容：

后面依然是两个例子和一些推荐文章。其中A3C算法似乎是比较火爆。

路漫漫其修远兮，吾将迟早听不懂。