最大伪森林——kruskal算法活用 (HDU - 3367)
- kruskal这一用来求生成树的算法,经过修改拓展之后,可以求很多种形式的子图,本题(HDU3367)即为一个应用案例
单击进入原题
- 以下是原题内容
Pseudoforest
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 4058 Accepted Submission(s): 1615
Problem Description
In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. The maximal pseudoforests of G are the pseudoforest subgraphs of G that are not contained within any larger pseudoforest of G. A pesudoforest is larger than another if and only if the total value of the edges is greater than another one’s.
Input
The input consists of multiple test cases. The first line of each test case contains two integers, n(0 < n <= 10000), m(0 <= m <= 100000), which are the number of the vertexes and the number of the edges. The next m lines, each line consists of three integers, u, v, c, which means there is an edge with value c (0 < c <= 10000) between u and v. You can assume that there are no loop and no multiple edges.
The last test case is followed by a line containing two zeros, which means the end of the input.
Output
Output the sum of the value of the edges of the maximum pesudoforest.
Sample Input
3 3
0 1 1
1 2 1
2 0 1
4 5
0 1 1
1 2 1
2 3 1
3 0 1
0 2 2
0 0
Sample Output
3
5
Source
“光庭杯”第五届华中北区程序设计邀请赛 暨 WHU第八届程序设计竞赛
Recommend
lcy
题意
-
本题介绍了一个“伪森林”的概念:
- 对一个无向图,如果它的一个子图满足每个连通分量内部至多有一个环,那么这一个子图就是该无向图的伪森林。
- 类比于最大生成树,如果在这个无向图中,某个伪森林所具有的边权之和大于等于所有此无向图的伪森林,那么该伪森林就叫做最大伪森林。
- 对一个无向图,如果它的一个子图满足每个连通分量内部至多有一个环,那么这一个子图就是该无向图的伪森林。
-
给我们一个无向图,要求我们求出它的最大伪森林所具有的边权之和。
思路
-
先思考如果每个连通分量没有环的情况,此时也就是求最大生成森林,此时由于并查集的重要作用,所以用kruskal算法非常合适
-
现在这个生成森林可以让每棵树至多存在一个环,显然我们的结果应该比简单的生成森林还要大一些。但是我们这样放弃kruskal算法是可惜的,我们可以对它进行修改来求出这个最大伪森林。
我们可能很容易想到,在kruskal算法算得最大生成森林之后,再把所有的边扫一遍,把上一次没有被选中的边(毫无疑问,这条边一定会构成一个环)再加入森林,同时通过并查集的祖先找到它所在的那棵树,标记这颗树为“有环”,这样之后每次判断没有环才会添加,就不会出现两个环了
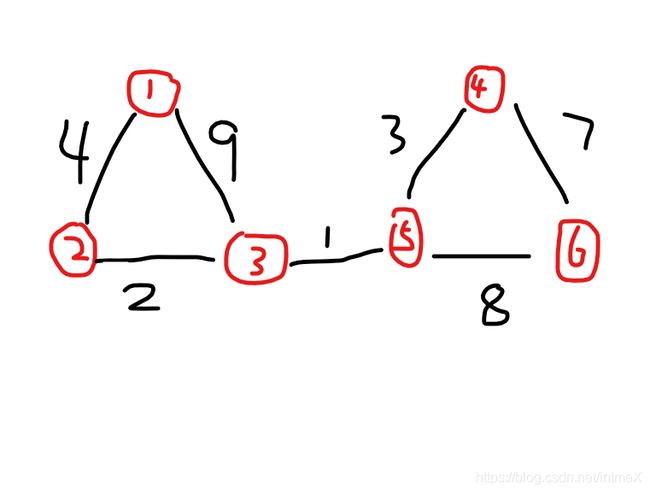
- 个人感觉上面我这个自己想出来的方法很具有迷惑性,因为由于边已经排好了序,容易让人认为没有更优情况了。不过仔细推敲就能发现反例,如下图:
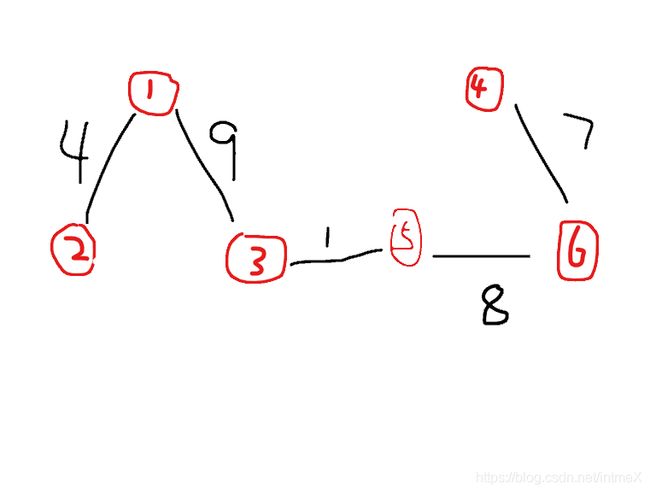
它的最大生成树是什么?(也就是说,我们第一步做完之后,得到的结果是什么?毫无疑问是下图:
那之后我们第二步加边之后 他会变成如下的一个伪森林:
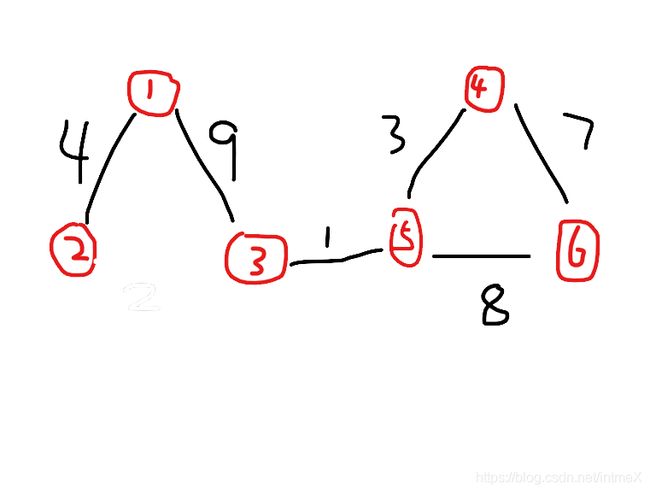
这是最大伪森林? 不是,下面这个才是:
这就否定了我们的想法
- 显然我们的设想是片面的,如果进行一次kruskal的最大生成森林,那么我们可以知道,出现的图都是“尽可能连通的”,也就是为了连通性牺牲了总权值。
但是最大伪森林不需要这样的牺牲,它完全可以去掉一条边来生成两棵树,进而选择到边权更大的边,只要每棵树不超过一个环,也就是可以牺牲一次连通性来换取更大的边权。
改进思路
- 注意我们在上面提到过“可以牺牲一次连通性来换取更大的边权。”,其实这个过程我们完全可以在kruskal算法的内部修改实现:
-
我们考虑把每棵树的有环情况实时记录,使用bk2数组,bk2[i]为true 表示并查集祖先为i的树目前有环。
-
仍然是边排序之后从头进行扫描,每次先路径压缩找到两个点所在树的祖先,然后通过bk2数组得知这两棵树的有无环情况。如果:
1.都是false无环
那么显然这条边可以被选中加入森林(不会违背任何条件)
要注意:如果这两棵树是同一颗,那么要标记这棵树为有环2.两棵都有环
那么不可以加入这条边,否则将会使生成的一棵树中有两个环3.一棵有环一棵无环
那么根据伪森林的定义,我们可以把这条边选入,但是要注意在之后把
要注意:如果这两棵树是同一棵,那么不可以加入(但事实上不可能出现这种情况,否则标记就是错误的)
-
- 其实实现上述逻辑之后,我们就已经成功地应用了伪森林的定义,结果即为最大伪森林的边权之和
AC代码
#include
#include
#include
#include
using namespace std;
int n, m, x, y, z, co = 1;
long long sum = 0;
struct ab //边
{
int u, v, w;
} aa[200005];
bool bk2[10005] = {0}; //某棵树有无环
int f[10005] = {0}; //并查集
bool cmp(ab a, ab b)
{
return a.w > b.w;
}
int fd(int xx) //路径压缩
{
if (f[xx] != xx)
{
f[xx] = fd(f[xx]);
}
return f[xx];
}
int main()
{
while (1)
{
scanf("%d%d", &n, &m);
if (!n && !m)
{
break;
}
memset(bk2, 0, sizeof(bk2));
for (int i = 1; i <= m; i++)
{
scanf("%d%d%d", &x, &y, &z);
aa[i].u = x;
aa[i].v = y;
aa[i].w = z;
}
for (int i = 0; i <= n; i++)
{
f[i] = i;
}
sort(aa + 1, aa + m + 1, cmp);
sum = 0;
for (int i = 1; i <= m; i++) //生成最大伪森林
{
if (fd(aa[i].u) == fd(aa[i].v))
{
if (bk2[f[aa[i].u]] || bk2[f[aa[i].v]])
{
continue;
}
else
{
bk2[f[aa[i].u]] = bk2[f[aa[i].v]] = true;
sum += aa[i].w;
}
}
else
{
if (bk2[f[aa[i].u]] && bk2[f[aa[i].v]])
{
continue;
}
sum += aa[i].w;
if (bk2[f[aa[i].u]] || bk2[f[aa[i].v]])
{
bk2[f[aa[i].u]] = true;
bk2[f[aa[i].v]] = true;
}
f[f[aa[i].v]] = f[aa[i].u];
}
}
printf("%lld\n", sum);
}
return 0;
}
解决本题的关键是理解好kruskal算法的性质(连通性为先,边权追求其次)以及对不同情况的全面分析