2020-7-18 吴恩达-改善深层NN-w1 深度学习的实用层面(课后编程1-Initialization-3种不同方法对比-He/MSRA初始化)
原文链接
如果打不开,也可以复制链接到https://nbviewer.jupyter.org中打开。
初始化 Initialization
- 1.NN模型
- 2.初始化为0
- 3.随机初始化
- 4.He初始化
- 5.结论
- 6.代码
欢迎来到改善深层NN的第一个编程作业。
训练NN需要指定权重初始值。一个好的初始化方法将有利于模型的学习。
如果你已经完成了前面的编程作业,那么你应该根据指导进行了权重初始化,到目前为止它已经成功运行。
但是对于一个新的NN你如何初始化呢?通过本作业,你将会了解不同的初始化将会有怎样不同的结果。
一个好的初始化能够
- 加速梯度下降的收敛
- 增加梯度下降收敛到较低训练误差(和泛化误差)的几率
关于权重的初始化,请参考 https://blog.csdn.net/u012328159/article/details/80025785
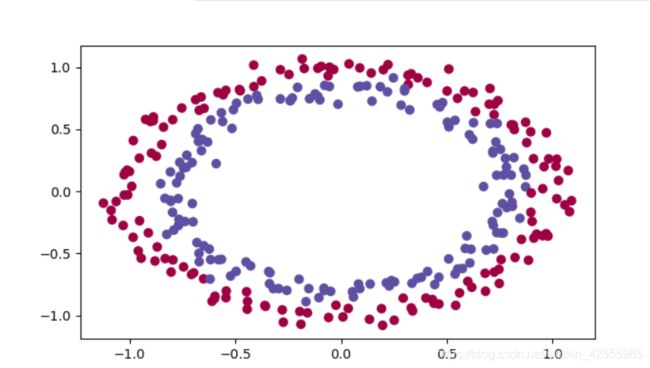
我们先运行以下代码来加载库和你用来分类的平面数据集
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
from init_utils import sigmoid, relu, compute_loss, forward_propagation, backward_propagation
from init_utils import update_parameters, predict, load_dataset, plot_decision_boundary, predict_dec
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# load image dataset: blue/red dots in circles
train_X, train_Y, test_X, test_Y = load_dataset()
说明:load_dataset()函数在init_utils.py中,内容如下
def load_dataset():
np.random.seed(1)
train_X, train_Y = sklearn.datasets.make_circles(n_samples=300, noise=.05)
np.random.seed(2)
test_X, test_Y = sklearn.datasets.make_circles(n_samples=100, noise=.05)
# Visualize the data
plt.scatter(train_X[:, 0], train_X[:, 1], c=train_Y, s=40, cmap=plt.cm.Spectral);
train_X = train_X.T
train_Y = train_Y.reshape((1, train_Y.shape[0]))
test_X = test_X.T
test_Y = test_Y.reshape((1, test_Y.shape[0]))
plt.show()
return train_X, train_Y, test_X, test_Y
你需要一个分类器来区分上图中的蓝色点和红色点。
1.NN模型
你将使用一个3层NN(前面已经实现)。以下是你要尝试的初始化方法
- 初始化为0:输入参数中设置
initialization = "zeros" - 随机初始化:输入参数中设置
initialization = "random"。这里初始化权重一个大的随机值。 - He初始化:输入参数中设置
initialization = "He"。这将权重初始化为根据何恺明等人2015年的论文缩放的随机值。- 关于何恺明的文章,Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification, Technical report, arXiv, Feb. 2015,参见链接。
- 这个初始化的目的是为了减少梯度爆炸和过快消失,抑制梯度异常。
- 这种初始化又叫MSRA初始化,它是一个均值为0方差为2/n的高斯分布。现在深度学习中常用的隐藏层激活函数是ReLU,因此常用的初始化方法就是这种方法。
- 顺便说一下,适用于激活函数是sigmoid和tanh的权重初始化方法是:
Xavier/Glorot Initialization
请快速看一下以下代码,并运行一下。后面会利用model()函数来调用3种不同的初始化方法
def model(X, Y, learning_rate=0.01, num_iterations=15000, print_cost=True, initialization="he"):
"""
实现一个三层的神经网络
Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.
Arguments:
X -- input data, of shape (2, number of examples) 输入的数据,维度为(2, 样本数量)
Y -- true "label" vector (containing 0 for red dots; 1 for blue dots), of shape (1, number of examples)
learning_rate -- learning rate for gradient descent 学习率
num_iterations -- number of iterations to run gradient descent 迭代的次数
print_cost -- if True, print the cost every 1000 iterations
字符串类型,权重初始化的类型【"zeros" | "random" | "he"】
initialization -- flag to choose which initialization to use ("zeros","random" or "he")
Returns:
parameters -- parameters learnt by the model 学习后的参数
"""
grads = {}
costs = [] # to keep track of the loss
m = X.shape[1] # number of examples
layers_dims = [X.shape[0], 10, 5, 1]
# Initialize parameters dictionary. 选择初始化参数的类型
if initialization == "zeros":
parameters = initialize_parameters_zeros(layers_dims)
elif initialization == "random":
parameters = initialize_parameters_random(layers_dims)
elif initialization == "he":
parameters = initialize_parameters_he(layers_dims)
# Loop (gradient descent)
for i in range(0, num_iterations):
#前向传播
# Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
a3, cache = forward_propagation(X, parameters)
# Loss 计算成本
cost = compute_loss(a3, Y)
# Backward propagation. 反向传播
grads = backward_propagation(X, Y, cache)
# Update parameters. 更新参数
parameters = update_parameters(parameters, grads, learning_rate)
# Print the loss every 1000 iterations
if print_cost and i % 1000 == 0:
print("Cost after iteration {}: {}".format(i, cost))
costs.append(cost)
# plot the loss 绘制成本曲线
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
2.初始化为0
在NN中有2个类型参数要初始化
- 权重矩阵( W [ 1 ] W^{[1]} W[1], W [ 2 ] W^{[2]} W[2], W [ 3 ] W^{[3]} W[3],…, W [ L − 1 ] W^{[L-1]} W[L−1], W [ L ] W^{[L]} W[L])
- 偏置向量( b [ 1 ] b^{[1]} b[1], b [ 2 ] b^{[2]} b[2], b [ 3 ] b^{[3]} b[3],…, b [ L − 1 ] b^{[L-1]} b[L−1], b [ L ] b^{[L]} b[L])
实现以下函数,把所有参数初始化为0。稍后你会看到它不能很好地工作,因为它不能“破坏对称性break symmetry”(对称性问题,参见链接),这里只是尝试一下,看看会发生说明。使用np.zeros((…,…))初始化参数,注意这里有两层括号。
def initialize_parameters_zeros(layers_dims):
"""
Arguments:
layer_dims -- python array (list) containing the size of each layer.
列表,模型的层数对应每一层节点的数
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
b1 -- bias vector of shape (layers_dims[1], 1)
...
WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
bL -- bias vector of shape (layers_dims[L], 1)
"""
parameters = {}
#网络层数,包含了输入层
L = len(layers_dims) # number of layers in the network
for l in range(1, L):
### START CODE HERE ### (≈ 2 lines of code)
parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l - 1]))
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
### END CODE HERE ###
return parameters
测试一下
parameters = initialize_parameters_zeros([3,2,1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
结果
W1 = [[0. 0. 0.]
[0. 0. 0.]]
b1 = [[0.]
[0.]]
W2 = [[0. 0.]]
b2 = [[0.]]
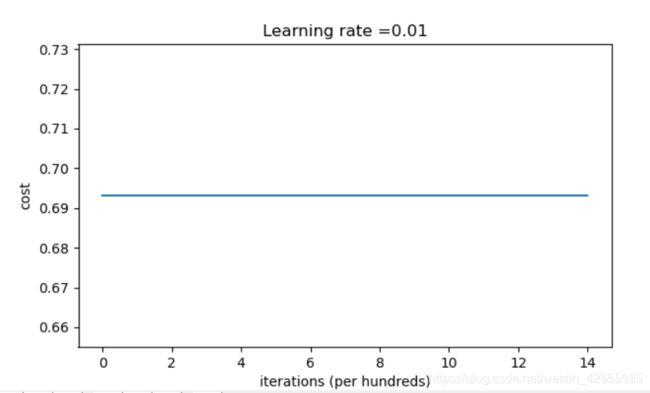
运行以下代码,使用0值初始化,迭代15000次训练你的模型。
parameters = model(train_X, train_Y, initialization = "zeros")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
结果如下
Cost after iteration 0: 0.6931471805599453
Cost after iteration 1000: 0.6931471805599453
Cost after iteration 2000: 0.6931471805599453
Cost after iteration 3000: 0.6931471805599453
Cost after iteration 4000: 0.6931471805599453
Cost after iteration 5000: 0.6931471805599453
Cost after iteration 6000: 0.6931471805599453
Cost after iteration 7000: 0.6931471805599453
Cost after iteration 8000: 0.6931471805599453
Cost after iteration 9000: 0.6931471805599453
Cost after iteration 10000: 0.6931471805599455
Cost after iteration 11000: 0.6931471805599453
Cost after iteration 12000: 0.6931471805599453
Cost after iteration 13000: 0.6931471805599453
Cost after iteration 14000: 0.6931471805599453
On the train set:
Accuracy: 0.5
On the test set:
Accuracy: 0.5
模型的性能很差(准确率50%),成本没有真正减少,算法的性能还不如随机猜。
这是为什么呢?我们来看一下预测的细节和决策边界。
print("predictions_train = " + str(predictions_train))
print("predictions_test = " + str(predictions_test))
运行结果
predictions_train = [[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0]]
predictions_test = [[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]
决策边界
plt.title("Model with Zeros initialization")
axes = plt.gca()
axes.set_xlim([-1.5, 1.5])
axes.set_ylim([-1.5, 1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
plt.show()
这个模型对于所有样本的预测结果都是0。
一般来说,把所有权重都初始化为0会导致NN无法破坏对称。
这意味这每层的每个神经元都学习了相同的东西,你也可以用每层的输入 n [ l ] = 1 n^{[l]}=1 n[l]=1 来训练NN,并且网络并没有比线性分类器(如逻辑回归)强大。
- 权重 W [ l ] W^{[l]} W[l]应该通过随机初始化来打破对称。
- 但是偏置 b [ l ] b^{[l]} b[l] 初始化为0是可以的。只要权重 W [ l ] W^{[l]} W[l] 随机初始化,对称依然可以被打破。
3.随机初始化
为了打破对称,我们要进行随机初始化权重。随机初始化之后,每个神经元可以继续学习输入的不同功能。在这个练习中,你会看到如果权重随机初始化为一个很大的值会发生什么。
实现以下函数,把你的权重初始化为10倍随机值,偏置初始化为0。
使用np.random.randn(..,..) * 10初始化权重,使用np.zeros((.., ..))初始化偏置。
我们使用固定的np.random.seed(..)确保你的随机权重会和我们的匹配,所以不用担心,即使你运行了很多次,你的代码都会给你相同的初始化参数值。
# GRADED FUNCTION: initialize_parameters_random
def initialize_parameters_random(layers_dims):
"""
Arguments:
列表,模型的层数对应每一层节点的数
layer_dims -- python array (list) containing the size of each layer.
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
b1 -- bias vector of shape (layers_dims[1], 1)
...
WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
bL -- bias vector of shape (layers_dims[L], 1)
"""
#指定随机种子
np.random.seed(3) # This seed makes sure your "random" numbers will be the as ours
parameters = {}
L = len(layers_dims) # integer representing the number of layers 网络层数,包含了输入层
for l in range(1, L):
### START CODE HERE ### (≈ 2 lines of code)
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * 10
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
### END CODE HERE ###
return parameters
测试一下
parameters = initialize_parameters_random([3, 2, 1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
运行结果
W1 = [[ 17.88628473 4.36509851 0.96497468]
[-18.63492703 -2.77388203 -3.54758979]]
b1 = [[0.]
[0.]]
W2 = [[-0.82741481 -6.27000677]]
b2 = [[0.]]
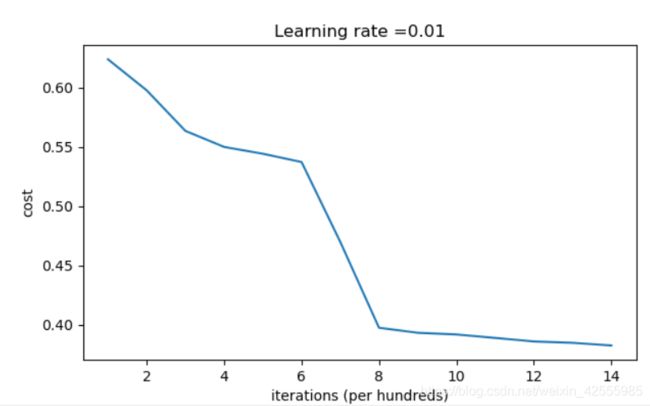
运行以下代码,使用随机初始化,迭代15000次训练你的模型。
parameters = model(train_X, train_Y, initialization = "random")
print("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
运行结果
Cost after iteration 0: inf
Cost after iteration 1000: 0.6239567039908781
Cost after iteration 2000: 0.5978043872838292
Cost after iteration 3000: 0.563595830364618
Cost after iteration 4000: 0.5500816882570866
Cost after iteration 5000: 0.5443417928662615
Cost after iteration 6000: 0.5373553777823036
Cost after iteration 7000: 0.4700141958024487
Cost after iteration 8000: 0.3976617665785177
Cost after iteration 9000: 0.39344405717719166
Cost after iteration 10000: 0.39201765232720626
Cost after iteration 11000: 0.38910685278803786
Cost after iteration 12000: 0.38612995897697244
Cost after iteration 13000: 0.3849735792031832
Cost after iteration 14000: 0.38275100578285265
On the train set:
Accuracy: 0.83
On the test set:
Accuracy: 0.86
上面的运行结果中,“inf”是迭代0次的成本,这是因为数值舍入。一个更复杂的数学实现可以解决这个问题。但是对我们目的来说这不用担心。
随机初始化结果,准确率超过了80%,打破了对称性,获得了更好的结果。对比初始化为0,模型的输出不再是全部为0。
看一下预测细节
print(predictions_train)
print(predictions_test)
结果
[[1 0 1 1 0 0 1 1 1 1 1 0 1 0 0 1 0 1 1 0 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 1
1 1 1 1 1 1 1 0 1 1 1 1 0 1 0 1 1 1 1 0 0 1 1 1 1 0 1 1 0 1 0 1 1 1 1 0
0 0 0 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 0 0 1 1 1 0 1 1 0 1 0 1 1 0 1 1 0
1 0 1 1 0 0 1 0 0 1 1 0 1 1 1 0 1 0 0 1 0 1 1 1 1 1 1 1 0 1 1 0 0 1 1 0
0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 0 1 1 0 1 0 1 1 1 1 0 1 1 1
1 0 1 0 1 0 1 1 1 1 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 0 1 1 1 0 1 0 1 0 0 1
0 1 1 0 1 1 0 1 1 0 1 1 1 0 1 1 1 1 0 1 0 0 1 1 0 1 1 1 0 0 0 1 1 0 1 1
1 1 0 1 1 0 1 1 1 0 0 1 0 0 0 1 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 1
1 1 1 1 0 0 0 1 1 1 1 0]]
[[1 1 1 1 0 1 0 1 1 0 1 1 1 0 0 0 0 1 0 1 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 1
0 1 1 0 0 1 1 1 1 1 0 1 1 1 0 1 0 1 1 0 1 0 1 0 1 1 1 1 1 1 1 1 1 0 1 0
1 1 1 1 1 0 1 0 0 1 0 0 0 1 1 0 1 1 0 0 0 1 1 0 1 1 0 0]]
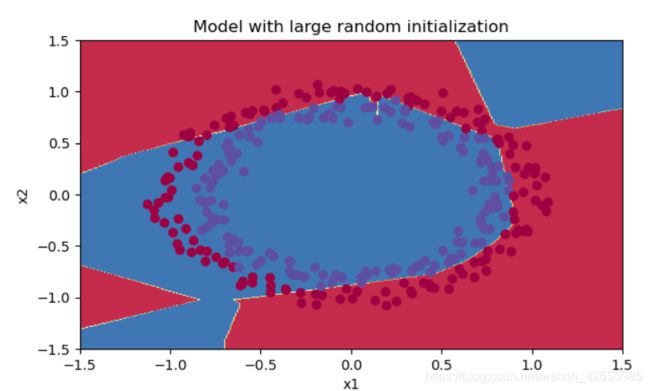
决策边界
plt.title("Model with large random initialization")
axes = plt.gca()
axes.set_xlim([-1.5, 1.5])
axes.set_ylim([-1.5, 1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
plt.show()
说明:
- 成本开始时候非常高,这是因为初始随机值很大。对于一些样本最后激活函数(sigmoid函数)的输出接近0或者1,而当一个样本出现错误时,会导致该样本的损失非常高。事实上,当输出层的输出 log ( a [ 3 ] ) = log ( 0 ) \log(a^{[3]}) = \log(0) log(a[3])=log(0), 损失会无穷大。
- 糟糕的初始化会导致梯度消失或者爆炸,也会减慢算法优化。
- 如果你对这个网络进行更长时间的训练,你将看到更好的结果,但是使用过大的随机数初始化会减慢优化的速度。
- 初始化为非常大随机值效果并不好
- 希望小的随机值可以效果好一点。问题是:随机值要多小才行呢?请看下面。
4.He初始化
最后,尝试He初始化,前面已经介绍过,有兴趣的可以查查何恺明。它十分类似于Xavier初始化。 Xavier 初始化使用的比例因子是sqrt(1./layers_dims[l-1]) ,适用于激活函数是sigmoid和tanh,而He初始化使用的是 sqrt(2./layers_dims[l-1])。
实现函数类似前面的initialize_parameters_random(…),唯一不同的是用10替代np.random.randn(…,…) ,然后用它乘以 2 上一层的维度 \sqrt{\frac{2}{\text{上一层的维度}}} 上一层的维度2。He初始化被推荐用于Relu激活函数。
实现代码如下
# GRADED FUNCTION: initialize_parameters_he
def initialize_parameters_he(layers_dims):
"""
Arguments:
layer_dims -- python array (list) containing the size of each layer.
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
b1 -- bias vector of shape (layers_dims[1], 1)
...
WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
bL -- bias vector of shape (layers_dims[L], 1)
"""
np.random.seed(3)
parameters = {}
# 网络层数,包含了输入层
L = len(layers_dims) - 1 # integer representing the number of layers
for l in range(1, L + 1): # 1 -> L-1,如果L=4,则只有W1,b1……W3,b3.
### START CODE HERE ### (≈ 2 lines of code)
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(2 / layers_dims[l - 1])
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
### END CODE HERE ###
return parameters
测试一下
parameters = initialize_parameters_he([2, 4, 1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
结果如下
W1 = [[ 1.78862847 0.43650985]
[ 0.09649747 -1.8634927 ]
[-0.2773882 -0.35475898]
[-0.08274148 -0.62700068]]
b1 = [[0.]
[0.]
[0.]
[0.]]
W2 = [[-0.03098412 -0.33744411 -0.92904268 0.62552248]]
b2 = [[0.]]
和前面2个初始化方法一样,运行以下代码,使用随机初始化,迭代15000次训练你的模型。
parameters = model(train_X, train_Y, initialization = "he")
print("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
运行结果
Cost after iteration 0: 0.8830537463419761
Cost after iteration 1000: 0.6879825919728063
Cost after iteration 2000: 0.6751286264523371
Cost after iteration 3000: 0.6526117768893807
Cost after iteration 4000: 0.6082958970572938
Cost after iteration 5000: 0.5304944491717495
Cost after iteration 6000: 0.4138645817071794
Cost after iteration 7000: 0.3117803464844441
Cost after iteration 8000: 0.23696215330322562
Cost after iteration 9000: 0.18597287209206836
Cost after iteration 10000: 0.15015556280371817
Cost after iteration 11000: 0.12325079292273552
Cost after iteration 12000: 0.09917746546525932
Cost after iteration 13000: 0.08457055954024274
Cost after iteration 14000: 0.07357895962677362
On the train set:
Accuracy: 0.9933333333333333
On the test set:
Accuracy: 0.96
看准确率就知道效果应该前2种初始化方法好。
再来看看决策边界
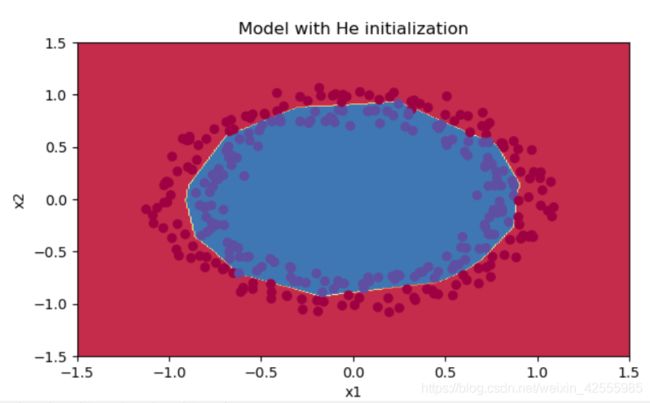
plt.title("Model with He initialization")
axes = plt.gca()
axes.set_xlim([-1.5, 1.5])
axes.set_ylim([-1.5, 1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
plt.show()
有没有发现,在15000次迭代后,红色和蓝色点基本被分开了。
5.结论
你已经看到了3种初始化方法。同样迭代次数,同样的超参(网络层数,学习率)对比如下
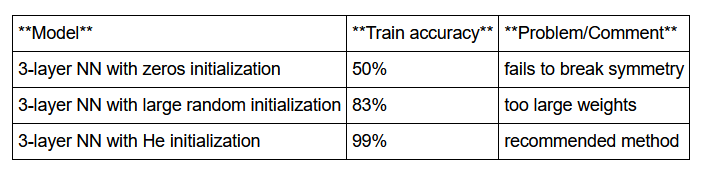
- 不同初始化方法获得不同的结果
- 随机初始化被用于打破对称性,它可以确保不同的隐藏单元可以学习到不同的东西
- 不要使用太大的值初始化
- He初始化在Relu激活函数效果很好
6.代码
全部代码下载