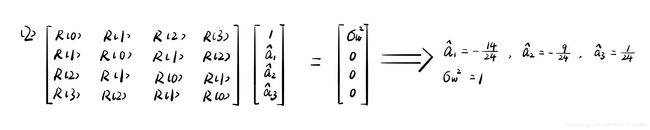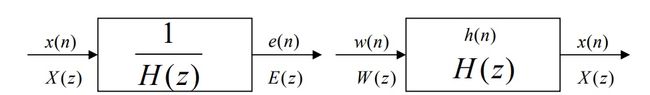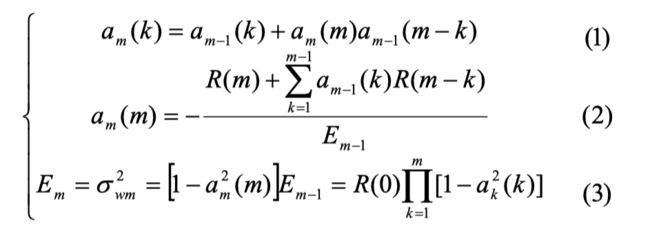AR模型的参数估计
AR模型的参数估计
一、AR模型概述
AR模型属于随机信号参数模型的一种。在AR模型中，随机信号x(n)由本身的若干次过去值x(n−k)和当前的激励值w(n)线性组合产生。
x ( n ) = w ( n ) − ∑ k = 1 p a k x ( n − k ) (1) x(n) = w(n) − \sum_{k=1}^{p} a_k x(n − k ) \tag{1} x(n)=w(n)−k=1∑pakx(n−k)(1)
该模型的系统函数：
H ( z ) = 1 1 + ∑ k = 1 p a k z − k (2) H(z)=\frac{1}{1+\sum_{k=1}^{p} a_k z^{-k}}\tag{2} H(z)=1+∑k=1pakz−k1(2)
p是系统阶数，系统函数中只有极点，无零点，也称为全极点模型，系统由于极点的原因，
要考虑到系统的稳定性，因而要注意极点的分布位置，用 AR（p）来表示。
信号的现代建模方法（Modern modeling method for signal）是建立在具有最大的不确定性基础上的预测。提出了众多的数学模型( mathematical models)。根据 Wold 的证明：任何 平稳的 ARMA（自回归移动平均）模型或 MA 模型均可用无限阶或阶数足够的 AR 模型去 近似。因此本节着重介绍 AR 模型的基本原理和方法。
二、AR模型的参数估计
1. AR模型参数与自相关函数的关系
1.1 推导过程
1.2 举例说明
【例 1】已知自回归信号模型 AR（3）为：
x ( n ) = 14 24 x ( n − 1 ) + 9 24 x ( n − 2 ) − 1 24 x ( n − 3 ) + w ( n ) x(n)=\frac{14}{24}x(n-1)+\frac{9}{24}x(n-2)-\frac{1}{24}x(n-3)+w(n) x(n)=2414x(n−1)+249x(n−2)−241x(n−3)+w(n)
式中 w( n ) 是具有方差 σ w 2 = 1 σ_{w}^2 =1 σw2=1 的平稳白噪声，求
a.自相关序列 R x x ( m ) Rxx (m) Rxx(m) ，m＝0，1，2，3，4，5。
b.用 a 求出的自相关序列来估计 AR（3）的参数 a ^ k \hat a_k a^k，以及输入白噪声的方差 σ w 2 = 1 σ_{w}^2 =1 σw2=1 大小。
c.利用给出的 AR 模型，用计算机仿真给出 32 点观测值
x(n)＝[0.4282 1.1454
1.5597 1.8994 1.6854 2.3075 2.4679 1.9790 1.6063 1.2804
-0.2083 0.0577 0.0206 0.3572 1.6572 0.7488 1.6666 1.9830
2.6914 1.2521 1.8691 1.6855 0.6242 0.1763 1.3490 0.6955
1.2941 1.0475 0.4319 0.0312 0.5802 -0.6177]，用观测值的自相关序
列直接来估计 AR(3)的参数 a ^ k {\hat a_k} a^k 以及输入白噪声的 σ w 2 σ_w^2 σw2 。
1.2.1 自相关序列 R x x ( m ) R_{xx}(m) Rxx(m) ，m＝0，1，2，3，4，5。
解得：
Rxx（m） =
4.9377
4.3287
4.1964
3.8654
3.6481
3.4027
1.2.2 已知自相关序列值，来估计 3 阶 AR 模型的参数 {a_k} 以及 σ w 2 σ_{w}^2 σw2
1.2.3 利用给出的 32 点观测值，求自相关序列
clear; clc;
xn = [0.4282 1.1454 1.5597 1.8994 1.6854 2.3075 2.4679 1.9790...
1.6063 1.2804 -0.2083 0.0577 0.0206 0.3572 1.6572 0.7488...
1.6666 1.9830 2.6914 1.2521 1.8691 1.6855 0.6242 0.1763...
1.3490 0.6955 1.2941 1.0475 0.4319 0.0312 0.5802 -0.6177];
Rxx_2 = xcorr(xn) ./ length(xn);
Rxx_2 = Rxx_2(length(xn) : end)
结果：
Rxx_2 =
1.9271 1.6618 1.5381 1.3545 1.1349 0.9060 0.8673 0.7520
0.7637 0.8058 0.8497 0.8761 0.9608 0.8859 0.7868 0.7445
0.6830 0.5808 0.5622 0.5134 0.4301 0.3998 0.3050 0.2550
0.1997 0.1282 0.0637 0.0329 -0.0015 -0.0089 -0.0143 -0.0083
把头 4 个相关序列值代入矩阵求得的估计值与真实 AR 模型参数误差为： e 1 e_1 e1＝0.1151， e 2 e_2 e2＝0.1002， e 3 e_3 e3＝0.0498，原因在于我们只有一部分的观测数据，使得自相关序列值与理想的完全不同。输入信号的方差误差比较大： e σ e_\sigma eσ＝0.5322，造成的原因比较多，计算机仿真的白噪声由于只有 32 点长，32 点序列的方差不可能刚好等于 1。给出一段观测值求 AR 模型参数这样直接解方程组，当阶数越高时直接解方程组计算就越复杂，因而要用特殊的算法使得计算量减小且精确度高。
2. Y－W 方程的解法——L-D 算法
2.1 准备工作
在求解上述例子时要得到更精确的估计值，就要建立更高阶的 AR 模型，直接用观测值的自相关序列来求解 Y-W 方程计算量太大。因此把 AR 模型和预测系统联系起来，换个方法来估计 AR 参数。
从 AR 模型的时域表达式：
x ( n ) = w ( n ) − ∑ k = 1 p a k x ( n − k ) x(n) = w(n) − \sum_{k=1}^{p} a_k x(n − k ) x(n)=w(n)−k=1∑pakx(n−k)我们知道模型的当前输出值与它过去的输出值有关。预测是推断一个给定序列的未来值，即利用信号前后的相关性来估计未来的信号值。
若序列的模型已知而用过去观测的数据来推求现在和将来的数据称为前向预测器，表示：
x ^ ( n ) = − ∑ k = 1 m a m ( k ) x ( n − k ) (3) \hat x(n) =− \sum_{k=1}^{m} a_m (k)x(n − k )\tag{3} x^(n)=−k=1∑mam(k)x(n−k)(3)
其中 a ( k ) {a_(k)} a(k),k=1,2,⋯,m{a(k)}，表示m阶预测器的预测系数，负号是为了与技术文献保持一致。显然预测出来的结果与真实的结果存在预测误差（或前向预测误差），设误差为 e ( n ) e(n) e(n)：
e ( n ) = x ( n ) − x ^ ( n ) = x ( n ) + ∑ k = 1 m a m ( k ) x ( n − k ) (4) e(n)=x(n)-\hat x(n)=x(n)+\sum_{k=1}^{m} a_m (k)x(n − k )\tag{4} e(n)=x(n)−x^(n)=x(n)+k=1∑mam(k)x(n−k)(4)
把e(n)看成是系统的输出， x(n)看成是系统的输入，得到系统函数：
E ( z ) X ( z ) = 1 + ∑ k = 1 m a m ( k ) z − k (5) \frac {E(z)}{X(z)}=1+\sum_{k=1}^{m} a_m (k)z^{-k}\tag{5} X(z)E(z)=1+k=1∑mam(k)z−k(5)
设m=p，且预测系数和 AR 模型参数相同，比较式(1)和式(5)，把预测误差系统框图和 AR 模型框图给出：
即有 w ( n ) = e ( n ) w(n)=e(n) w(n)=e(n) ，即前向预测误差系统中的输入为x(n) ，输出为预测误差e(n) 等于白噪声。也就是说前向预测误差系统对观测信号起了白化的作用。由于 AR 模型和前向预测误差系统有着密切的关系，两者的系统函数互为倒数，所以求 AR 模型参数就可以通过求预测误差系统的预测系数来实现。
2.2 使用L-D算法估计AR模型参数
经过一系列推导，可以得到预测系数和均方误差估计的通式：
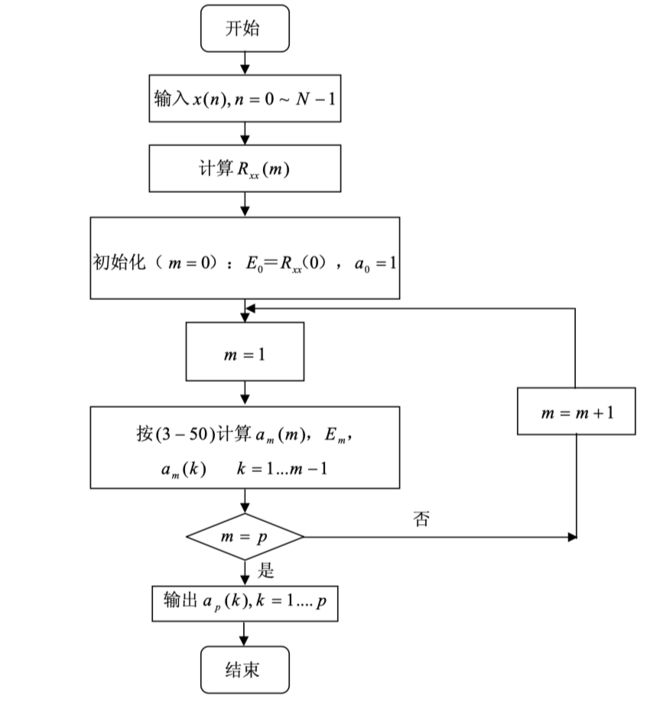
其中 a m ( m ) a_m (m) am(m)称为反射系数， 从上式知道整个迭代过程需要已知自相关函数， 给定初始值 E 0 = R ( 0 ) ， a 0 ( 0 ) = 1 E_0 = R(0) ， a_0 (0) = 1 E0=R(0)，a0(0)=1 ，以及 AR 模型的阶数 p ，就可以按照如下所示流程图进行估计：
2.3 L-D算法的特点
优点：
- 计算速度快
- 求得的AR模型必定稳定
- 且均方预测误差随着阶次的增加而减小
缺点：
- 有较大误差（原因：在求自相关序列时，假设是除了观测值之外的数据均为0）
2.4 L-D算法的Matlab实现
x_n = [0.4282 1.1454 1.5597 1.8994 1.6854 2.3075 2.4679 1.9790 1.6063 1.2804 -0.2083 0.0577 0.0206 0.3572 1.6572 0.7488 1.6666 1.9830 2.6914 1.2521 1.8691 1.6855 0.6242 0.1763 1.3490 0.6955 1.2941 1.0475 0.4319 0.0312 0.5802 -0.6177];
R_xx = zeros( 1, length(x_n) );
%Matlab从1开始计数，本例中所有下标为0的元素全部改为1计算，之后的元素同理顺延
%步骤1：求自相关序列
for m = 0 : length(x_n) - 1
i = 1;
while m + i <= length(x_n)
R_xx(m+1) = R_xx(m+1) + x_n(i) * x_n(i + m );
i = i + 1;
end
R_xx(m+1) = R_xx(m+1) / 32;
end
%步骤2：初始化
p = 4;
E = zeros(1, p);
E(1) = R_xx(1);
a = zeros(p, 3);
a(1 , 1) = 1;
a2=zeros(1,3);
%步骤3:计算
for m = 1:p-1
%计算a(m+1,m)
a( m + 1, m ) = R_xx(m + 1);
for k = 1:( m - 1 )
a( m + 1, m ) = a( m + 1, m ) + a( m, k ) * R_xx( m + 1 - k );
end
a( m + 1, m ) = - a( m + 1, m ) / E(m);
%计算a(m+1,k)
for k = 1:(m - 1)
a( m + 1, k ) = a( m, k ) + a( m + 1, m ) * a( m, m - k );
end
%计算E
E( m + 1 ) = ( 1 - a( m + 1, m ).^2 ) * E(m);
end
for k=1:3
a2(k)=a(4,k);
end
所得结果：
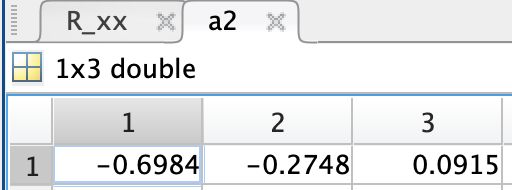
和例1的c结果一致，误差分析也一样。因此当计算阶数较高时，可以用递推程序实现。
Matlab 有专门的函数实现 L-D 算法的 AR 模型参数估计：[a E]＝aryule（x，p），输入 x表示观测信号，输入 p 表示要求的阶数，输出 a 表示估计的模型参数，e 表示噪声信号的方差估计。例如本题用该函数计算结果为：
[a, E]=aryule(x_n,p);
a =1.0000 -0.6984 -0.2748 0.0915
E = 0.4678
假如我们用更高阶的 AR 模型来估计：
[a E]=aryule(x,12)
a =1.0000 -0.6703 -0.3254 -0.0793 0.1407 0.3676 -0.2451 0.0483
-0.0912 -0.0522 0.0515 0.0186 -0.0955
E =0.3783
阶数越高均方误差越来越小。
三、AR 模型参数估计的各种算法的比较和阶数的选择
3.1 Burg算法
为了克服L-D算法导致的误差，1968年Burg提出了Burg算法，其基本思想是对观测的数据进行前向和后向预测，然后让两者的均方误差之和为最小作为估计的准则估计处反射系数，进而通过L-D算法的递推公式求出AR模型参数。Burg算法的优点是，求得的AR模型是稳定的，较高的计算效率，但递推还是用的L-D算法，因此仍然存在明显的缺点。
MATLAB中也有专门的函数来实现Burg算法的AR模型参数估计：[a E] = arburg(x_n, p)，例如上面例题中用Burg算法计算结果为：
p=3:
[a E]=arburg(x,3)
a =1.0000 -0.6982 -0.2626 0.0739
E =0.4567
p=12:
[a E]=arburg(x,12)
a =1.0000 -0.6495 -0.3066 -0.0934 0.0987 0.4076 -0.1786 -0.0126
-0.0805 -0.0899 0.0382 0.1628 -0.2501
E =0.3237
与L-D算法的结果略有不同，Burg算法略微更精确些。
3.2 Marple与FPE
