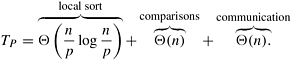cuda并行结构下的冒泡排序

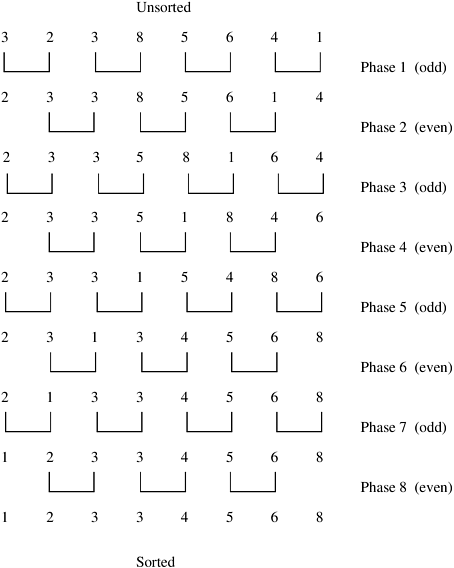
两两比较的冒泡排序

2n-1次 奇数和它右边的比较交换

2n次 偶数和他右边比较交换 

Algorithm 9.3 Sequential odd-even transposition sort algorithm.

1.   procedure ODD-EVEN(n) 
2.   begin 
3.      for i := 1 to n do 
4.      begin 
5.         if i is odd then 
6.              for j := 0 to n/2 - 1 do 
7.                  compare-exchange(a2j + 1, a2j + 2); 
8.         if i is even then 
9.              for j := 1 to n/2 - 1 do 
10.                 compare-exchange(a2j, a2j + 1); 
11.     end for 
12.  end ODD-EVEN 

Parallel Formulation

It is easy to parallelize odd-even transposition sort. During each phase of the algorithm, compare-exchange operations on pairs of elements are performed simultaneously. Consider the one-element-per-process case. Let n be the number of processes (also the number of elements to be sorted). Assume that the processes are arranged in a one-dimensional array. Element a_i initially resides on process P_i for i = 1, 2, ..., n. During the odd phase, each process that has an odd label compare-exchanges its element with the element residing on its right neighbor. Similarly, during the even phase, each process with an even label compare-exchanges its element with the element of its right neighbor. This parallel formulation is presented in Algorithm 9.4.

Algorithm 9.4 The parallel formulation of odd-even transposition sort on an n-process ring.

并行结构下的冒泡，基于刚才给出的奇偶比较法 

id即为线程号 第i个线程对应一个数列中的第i个数

1.   procedure ODD-EVEN_PAR (n) 
2.   begin 
3.      id := process's label 
4.      for i := 1 to n do 
5.      begin 
6.         if i is odd then 
7.             if id is odd then 
8.                 compare-exchange_min(id + 1); 
9.             else 
10.                compare-exchange_max(id - 1); 
11.        if i is even then 
12.            if id is even then 
13.                compare-exchange_min(id + 1); 
14.            else 
15.                compare-exchange_max(id - 1); 
16.     end for 
17.  end ODD-EVEN_PAR 

During each phase of the algorithm, the odd or even processes perform a compare- exchange step with their right neighbors. As we know from Section 9.1, this requires time Q(1). A total of n such phases are performed; thus, the parallel run time of this formulation is Q(n). Since the sequential complexity of the best sorting algorithm for n elements is Q(n log n), this formulation of odd-even transposition sort is not cost-optimal, because its process-time product is Q(n²).

To obtain a cost-optimal parallel formulation, we use fewer processes. Let p be the number of processes, where p < n. Initially, each process is assigned a block of n/p elements, which it sorts internally (using merge sort or quicksort) inQ((n/p) log(n/p)) time. After this, the processes execute p phases (p/2 odd and p/2 even), performing compare-split operations. At the end of these phases, the list is sorted (Problem 9.10). During each phase, Q(n/p) comparisons are performed to merge two blocks, and time Q(n/p) is spent communicating. Thus, the parallel run time of the formulation is