力扣 984 不包含aaa或bbb的字符串 python
给定两个整数 A 和 B,返回任意字符串 S,要求满足:
S 的长度为 A + B,且正好包含 A 个 ‘a’ 字母与 B 个 ‘b’ 字母;
子串 ‘aaa’ 没有出现在 S 中;
子串 ‘bbb’ 没有出现在 S 中。
示例 1:
输入:A = 1, B = 2
输出:“abb”
解释:“abb”, “bab” 和 “bba” 都是正确答案。
示例 2:
输入:A = 4, B = 1
输出:“aabaa”
提示:
0 <= A <= 100
0 <= B <= 100
对于给定的 A 和 B,保证存在满足要求的 S。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/string-without-aaa-or-bbb
这个题本来想用简单的循环暴力解,但是太麻烦还不能成功
用C写比较麻烦,C不能直接将字符之间加到字符串中,所有推荐python
大致思路都一样 贪心算法,
分类A>B
A=B
A
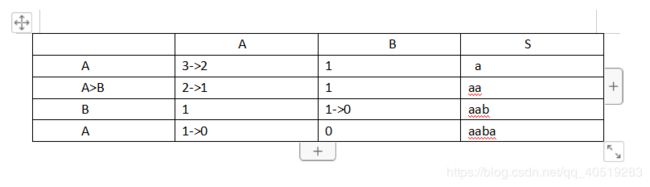
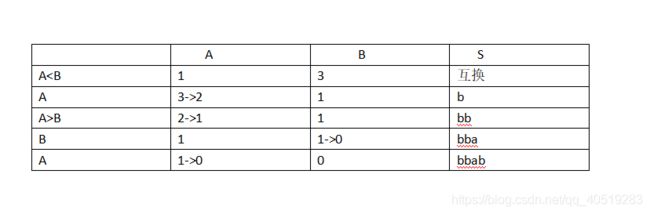
A>B时
判断A,B不空,A>B时,aab,否则ab即可
python:
def strWithout3a3b(self, A: int, B: int):
a='a'
b='b'
s=''
if(A==B):
return (a+b)*A
while A or B:
if A<B:
A,B=B,A
a,b=b,a
if A:
s=s+a
A=A-1
if A>B:
s=s+a
A=A-1
if B:
s=s+b
B=B-1
return s
C可以借助函数 strncat
char s[100]="hello world";
char s2[100]="abcefg";
//3.添加指定长度的字符串
strncat(s,s2,3);
还可以再优化
在A>B的情况下:
判断|A-B|与B的关系,若A-B的绝对值d大于B
则将(aab)(A-B)加入串中(此时在兼顾后面a,b个数且正确的情况下(A-B)时的aa最多)
然后再将’ab’(B2-A)添加到结果中
若A=11,B=7,A-B=4<7,虽然此时的aa最多数是5即10个a,但这样再加入ab时b只有6个
如果dif>B的话,我们首先将’aab’B添加到res中(因为此时aa的数量最多为B,并且此时我们的b也用完了),然后再将’a’(A-2B)添加到结果中。
class Solution:
def strWithout3a3b(self, A, B, a='a', b='b'):
"""
:type A: int
:type B: int
:rtype: str
"""
if A == B:
return (a+b)*B
if B > A:
A, B = B, A
a, b = b, a
if A >= B * 2:
return (a + a + b) * B + a * (A - B * 2)
return (a + a + b) * (A - B) + (a + b) * (B * 2 - A)
使用递归:
我们同样也只考虑三种情况,我们首先判断A>B,如果成立,我们返回a2+b+f(A-2,B-1),如果AB,我们返回(a+b)*A,如果A
class Solution:
def strWithout3a3b(self, A, B, a='a', b='b'):
"""
:type A: int
:type B: int
:rtype: str
"""
if B > A:
return self.strWithout3a3b(B, A, b, a)
if B == 0:
return a*A
if A > B:
return (a*2+b)+self.strWithout3a3b(A-2, B-1, a, b)
else:
return (a+b)+self.strWithout3a3b(A-1, B-1, a, b)
总结,看题最好先看出需要用到什么算法,数据结构,多加考虑,寻找题目规律,这个题就是aab与ab的相间分布,巧妙语言的特性,巧妙运用条件语句与判断语句,第一种方法中对条件语句的运用值得学习。
代码与思想部分借鉴于
https://blog.csdn.net/qq_17550379/article/details/86714870