并查集(Union-Find Algorithm)，看这一篇就够了

动态连接（Dynamic connectivity）的问题

所谓的动态连接问题是指在一组可能相互连接也可能相互没有连接的对象中，判断给定的两个对象是否联通的一类问题。这类问题可以有如下抽象：

• 有一组构成不相交集合的对象
• union: 联通两个对象
• find: 返回两个对象之间是否存在一条联通的通路
  ˇ
  在使用union-find处理动态连接的问题时，我们一般将这一组对象抽象为一个数组。

对于这组对象，其中相互连接的一些对象构成的子集称为联通集。

算法目的：能够在如下条件下高效解决动态连接的问题

• Union命令和Find命令可能交替被调用
• 操作的总数M可能很大
• 集合中的对象数目N可能很大

Quick find

数据结构：

• 输入数组id[]的长度为N。且每一个对象最初的id都为其本身。
• 当且仅当p和q具有相同的id时p和q才是联通的。
• id[]数组中存储对应对象所属的联通集的root的id。

算法：

• Union：欲将p和q相连，相当于合并包含p的联通集和包含q的联通集，也就是将所有id与id[p]相同的对象的id改为id[q]。
• Find：检查p和q的id是否相同即可。

示例：

对于下表所示的对象集合，如果我们调用union(1,3)，则需要将所有id为2的对象的id改为4。经过这个操作之后，原先的两个联通集[1,2]与[3,4]如今成为了一个联通集。

|  i    | 0 | 1 | 2 | 3 | 4 |
| id[i] | 0 | 2 | 2 | 4 | 4 |

==> 

|  i    | 0 | 1 | 2 | 3 | 4 |
| id[i] | 0 | 4 | 4 | 4 | 4 |

Quick find的Java实现

public class QuickFind {
    int[] id;
    public QuickFind(int n) {
        id = new int[n];
        for (int i = 0; i < n; i++) {
            id[i] = i;
        }
    }

    public void union(int p, int q) {
        int pid = id[p];
        int qid = id[q];
        for (int i = 0; i < this.id.length; i++) {
            if (id[i] == pid) {
                id[i] = qid;
            }
        }
    }

    public boolean find(int p, int q) {
        return id[p] == id[q];
    }
}

时间复杂度分析

• find()操作的时间复杂度为O(1)。
• union()操作的时间复杂度为O(N)。

Quick union

显而易见，Quick find算法太慢了。如果我们想要重复调用union()N次，时间复杂度将为O(N^2)。那么我们如何优化其时间复杂度呢？

我们可以采用称为lazy approach的方法来进行优化。所谓的lazy approach，也就是我们在设计算法的时候，对于一个步骤尽量减少其工作量，直到我们不得不进行这些工作的时候才进行。对于优化Quick find算法而言，就是我们尽量减少union()中的工作量，知道我们在调用find()的时候再去补上之前偷懒没有做的工作。那么我们如何减少union()中的工作量呢？

答案是：直到有必要前，我们并不改变一个联通集中的每一个元素的id。

在Quick find算法中，我们每一次union()操作都会将一个联通集中的每一个元素的id改为联通集中root元素的id。现在我们将其改变为仅仅将新元素所属的联通集的root的id改为另一个元素所属的联通集的root的id。直到我们需要判断两个元素是否连通的时候，也就是调用find()的时候，我们就寻找两个元素所属的联通集的root id是否相同。

数据结构：

• 输入数组id[]的长度为N。且每一个对象最初的id都为其本身。
• 当且仅当p和q具有相同的root id时p和q才是联通的。
• id[]数组中存储相应对象的parent的id。
• i的root为id[id[id[...id[i]...]]]。

算法：

• Union：欲将p和q相连，也就是将q所属的联通集融合为p所属的联通集的root的子联通集，即将q所属的联通集的root的id改为p所属的联通集的root的id。
• Find：检查p和q的root id是否相同。

示例：

对于下表所示的对象集合，如果我们调用union(1,3)，则需要将3所述的联通集的root的id改为1所属的联通集的root的id，也就是将id[4]改为2。

|  i    | 0 | 1 | 2 | 3 | 4 |
| id[i] | 0 | 2 | 2 | 4 | 4 |

==> 

|  i    | 0 | 1 | 2 | 3 | 4 |
| id[i] | 0 | 2 | 2 | 4 | 2 |

Quick union的Java实现

public class QuickUnion{
    int[] id;

    public QuickUnion(int n) {
        this.id = new int[n];
                for (int i = 0; i < n; i++) {
                    id[i] = i;
                }
    }

    public void union(int p, int q) {
        int rootP = getRoot(p);
        int rootQ = getRoot(q);
        id[rootQ] = rootP;
    }

    public boolean find(int p, int q) {
        return getRoot(p) == getRoot(q);
    }

    private int getRoot(int i) {
        while (i != id[i]) {
            i = id[i];
        }
        return i;
    }
}

时间复杂度分析

• find()操作的时间复杂度最坏情况下为O(N)。
• union()操作的时间复杂度最坏情况下为O(1)。

Quick union的表现将随着我们不断调用union()构建联通集而变差。因为代表这个联通集的树越来越高，调用getRoot()的开销也就越来越大。

Weighted Quick Union with Path Compression

通过以上的分析，我们得到了一个稍快的算法Quick union，但其时间复杂度会随着联通集所对应的树越来越高而变差。我们是否可以进一步优化这个算法呢？

答案是可以的。既然其表现随着树的高度增长而变差，那么我们就需要找出一些方法来使联通集所构造的树更加扁平。通过以下两种方法，我们可以大大减少树的高度。

Weighted Quick union

以Quick union为基础，我们额外利用一个sz[]保存每一个联通集中对象的数量。在调用union()的时候，我们总是把对象数目较少的联通集连接到对象数目较多的联通集中。通过这种方式，我们可以在一定程度上缓解树的高度太大的问题，从而改善Quick union的时间复杂度。

算法

• Union：在Quick union的基础上，将较小的联通集并入较大的联通集中。并且在合并之后更新sz[]数组中对应的联通集的大小。
• Find：与Quick union相同。

时间复杂度分析

• find()操作的时间复杂度最坏情况下为O(lgN)。
  原因在于我们每次都将包含对象较少的联通集连接到包含对象较大的联通集上，因此产生的联通集在最坏情况下的高度为O(lgN)。
• union()操作的时间复杂度最坏情况下为O(lgN)。
  原因与find()相同。

Path compression

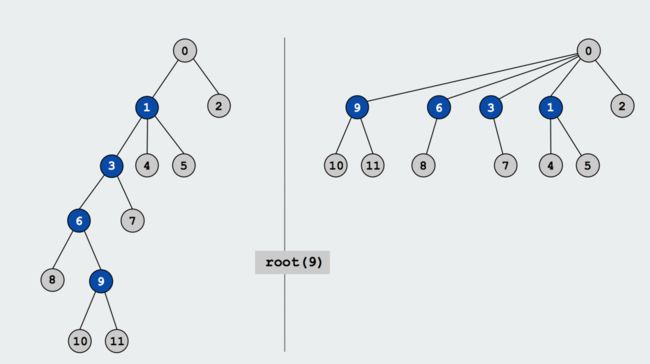
以Quick union为基础，在寻找对象i所对应的联通集的root的过程之后，将中途所检查过的每一个对象对应的id都改为root(i)。如下面的例子所示：

在实际代码实现的时候，为简单起见，我们并不将所有检查过的对象的id都改为root(i)，而是将每一个元素的id改为其parent的id。这样虽然无法完全将树扁平化，但可以达到近似的优化效果。

算法

• Union：在Quick union的基础上，每次在寻找某一个对象所对应的联通集的root的时候，将沿途遇到的每一个对象的id改为id[id[i]]。或者记录下root的id，用另一个循环来将沿途每一个对象的id改为root的id。
• Find：与Quick union相同。

时间复杂度分析

• union()：最坏情况下为O(lgN)。
• find()：最坏情况下为O(lgN)。

Weighted Quick Union with Path Compression时间复杂度分析

理论上，从一个完全不相连通的N个对象的集合开始，任意顺序的M次union()调用所需的时间为O(N+Mlg*N)。

其中lg*N称为迭代对数（iterated logarithm）。实数的迭代对数是指须对实数连续进行几次对数运算后，其结果才会小于等于1。这个函数增加非常缓慢，可以视为近似常数（例如2^65535的迭代对数为5）。

因此我们可以认为Weighed Quick Union with Path Compression是一个线性时间的算法。

Weighted Quick Union with Path Compression的Java实现

public class WeighedQuickUnionWithPathCompression{
    int[] id;
    int[] sz;

    public WeighedQuickUnionWithPathCompression(int n) {
        this.id = new int[n];
        this.sz = new int[n];
        for (int i = 0; i < n; i++) {
            id[i] = i;
            sz[i] = 1;
        }
    }

    public void union(int p, int q) {
        int rootP = getRoot(p);
        int rootQ = getRoot(q);

        // weighted quick union
        if (sz[rootP] >= sz[rootQ]) {
            id[rootQ] = rootP;
            sz[rootP] += sz[rootQ];
        } else {
            id[rootP] = rootQ;
            sz[rootQ] += sz[rootP];
        }
    }

    public boolean find(int p, int q) {
        return getRoot(p) == getRoot(q);
    }

    private int getRoot(int i) {
        while (i != id[i]) {
            // path compression
            id[i] = id[id[i]];
            i = id[i];
        }
        return i;
    }
}