数据结构——并查集Union Find
一、并查集解决了什么问题?
1、网络中节点间的连接状态:这里的网络是一个抽象的概念,指的是用户之间形成的网络
2、两个或两个以上集合之间的交集
二、对并查集的设计
对于一组数据,主要支持两个操作
public interface UnionFind {
//int getSize();
boolean isConnected(int p , int q);
void unionElements(int p , int q);
}
并查集版本1:Quick Find
并查集的基本数据表示
id为0、2、4、6、8它们都对应值0,所以可以认为它们属于同一个集合。这就解释了上面书写的方法isConnected(p,q),只要p和q的id所隐射的值是否一致即可,实际上就是find(p) == find(q)?,这种查询称为:Quick Find,它的时间复杂度:O(1)。
那么union合并这个操作是怎样的呢?
如上图所示,id为单数对应一个集合1,id为双数对应一个集合0,如果我们进行union(1,4),即把集合1与集合2进行合并,变为:
//version 1
public class UnionFind1 implements UnionFind{
//创建一个id数组
private int [] id;
public UnionFind1(int size){
id = new int[size];
for(int i = 0 ; i < id.length ; i++)
id[i] = i;
}
public int getSize() {
return id.length;
}
//查找元素p所对应的集合编号
private int find(int p){
if(p < 0 && p >= id.length)
throw new IllegalArgumentException("p is out of bound");
return id[p];
}
//查询元素p或元素p是否属于同一个集合
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
//合并元素p与元素q所属的集合
public void unionElements(int p, int q) {
int pId = find(p);
int qId = find(q);
//元素p和元素q已经所属同一个集合
if(pId == qId)
return ;
for(int i = 0 ; i < id.length ;i++){
if(id[i] == pId)
id[i] = qId;
}
}
}我们使用数组实现了版本1 Quick Find并查集的并查集,其中:
boolean isConnected(int p , int q); //时间复杂度O(1)
void unionElements(int p , int q); //时间复杂度O(n)下面我们使用树结构实现并查集,且这个树十分奇怪,是由孩子节点指向父节点的。
并查集版本2:使用树实现
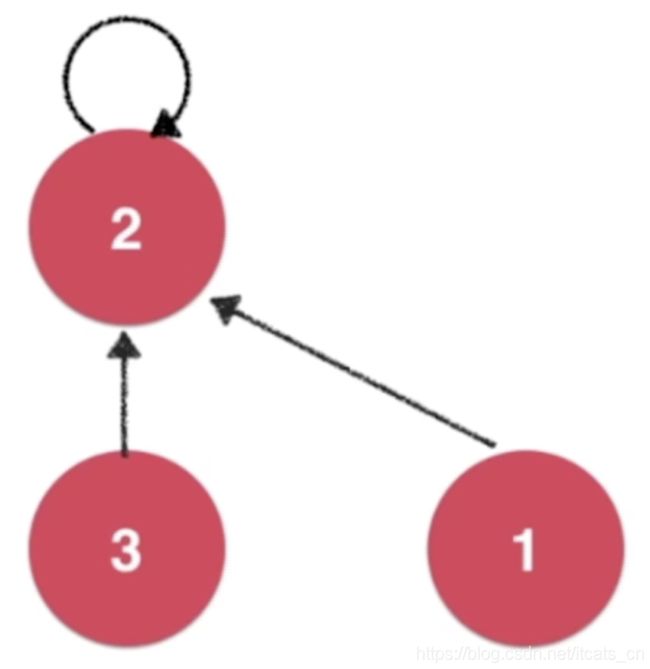
①我们将每一个元素看做是一个节点,图中节点3指向节点2,节点2作为根节点,对于节点2而言,它也有一个指针指向自己。
②如果节点1所对应的元素需要和节点3所对应的元素进行合并union,实际就是将节点1的指针指向节点3的根节点,如图:
③图中5是根节点,6和7都是5的孩子节点同时指向节点5,若想让7节点和2节点进行合并,则只需让7的根节点5指向2即可
如果想让节点7与节点3合并,实际图是一样的,即节点7的根节点5指向节点3的根节点2。
我们发现,每一个节点都只有一个指针,我们可以使用数组来表示这个指针的关系,在初始化的时候,我们让每一个节点都指向自己,如总共有10个元素:
严格来说我们的并查集并不是一个树形结构,而是一个森林。
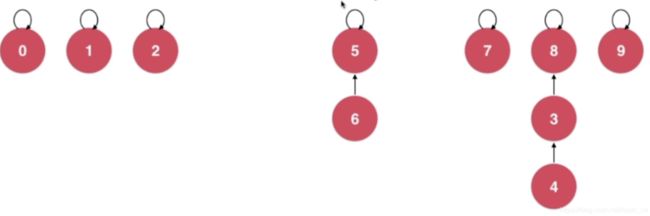
如果我们要union(4,3)的话,实际上就是将4的指针指向节点3
如果我们要union(3,8)的话,实际上就是将3的指针指向节点8
如果我们要union(6,5)的话,实际上就是将6的指针指向节点5
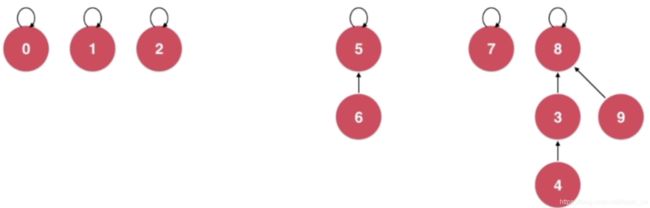
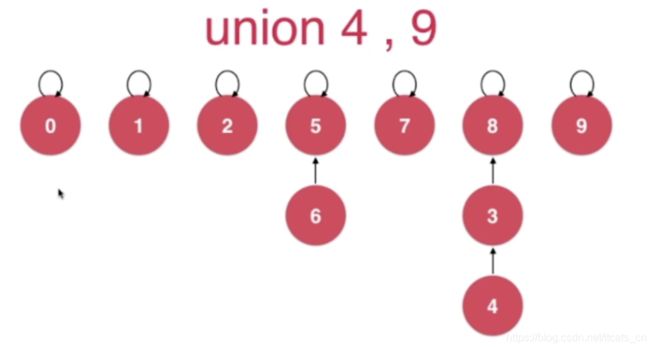
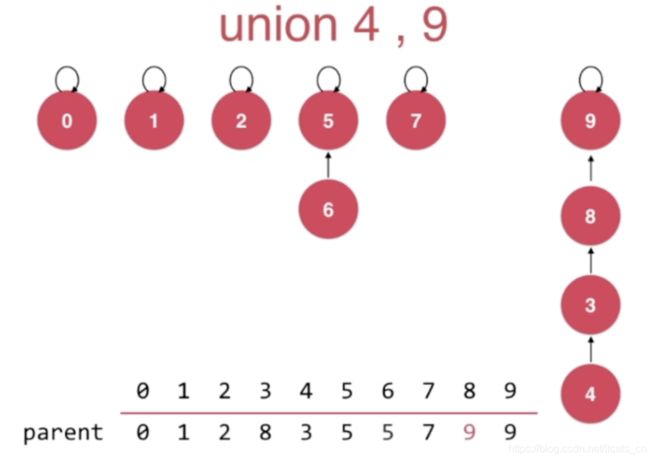
如果我们要union(9,4)的话,实际上就是将9的指针指向节点4所在树的根节点,此时就涉及一个查询操作了,查看上图中的数组图,4指向了3,3指向了8,而8指向了自己,那么就让节点9指向节点8
为什么我们不让节点9直接指向节点4呢?如果9指向4,实际就是生成一个链表,树的优势无法体现,现在节点9指向节点8,若我们需要查询节点9的根节点是什么?只需要一次查询即可,所以对应的数组图改变为:
实际上我们的这种数据结构中,union操作的时间复杂度为O(h),h为树的深度
public class UnionFind2 implements UnionFind{
//创建一个id数组
private int [] parent;
public UnionFind2(int size){
parent = new int[size];
for(int i = 0 ; i < parent.length ; i++)
parent[i] = i;
}
public int getSize() {
return parent.length;
}
//查找元素p所对应的集合编号
//O(h)复杂度,h为树的高度
private int find(int p){
if(p < 0 && p >= parent.length)
throw new IllegalArgumentException("p is out of bound");
while(p != parent[p])
p = parent[p];
return p;
}
//查询元素p或元素p是否属于同一个集合
//O(h)复杂度,h为树的高度
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
//合并元素p与元素q所属的集合
//O(h)复杂度,h为树的高度
public void unionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot)
return;
parent[pRoot] = qRoot;
}
}
并查集版本3:基于size进行优化
目前我们完成了两个版本的Union Find。在版本2中,find()方法时间复杂度是O(h) ,查询的过程实际上是一个不断索引的过程,需要在不同的地址空间完成跳转,在find次数过多的情况下,有可能造成union过程合并后树的高度h过大,造成查询性能降低。
慢的原因实际为:我们总让 parent[pRoot] = qRoot; 而并没有考虑过两个树的特点。于是我们考虑基于size进行优化,我们需要考虑合并的两棵树分别有多少个节点,如:
此时高度为4,我们完全可以让节点9指向4所在的根节点,这样高度仅为3。
让节点个数少的树的根节点指向节点个数多的树的根节点,这样union后所形成的树深度较低。
具体编程优化:
public class UnionFind3 implements UnionFind{
//创建一个id数组
private int [] parent;
//新增一个数组
private int[] sz; //表示以i为根的集合中元素的个数
public UnionFind3(int size){
sz = new int[size]; //对sz进行初始化
parent = new int[size];
for(int i = 0 ; i < parent.length ; i++) {
parent[i] = i;
sz[i] = 1;
}
}
public int getSize() {
return parent.length;
}
//查找元素p所对应的集合编号
//O(h)复杂度,h为树的高度
private int find(int p){
if(p < 0 && p >= parent.length)
throw new IllegalArgumentException("p is out of bound");
while(p != parent[p])
p = parent[p];
return p;
}
//查询元素p或元素p是否属于同一个集合
//O(h)复杂度,h为树的高度
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
//合并元素p与元素q所属的集合
//O(h)复杂度,h为树的高度
public void unionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot)
return;
if(sz[pRoot] < sz[qRoot]){
parent[pRoot] = qRoot;
sz[qRoot] += sz[pRoot];
}else{
parent[qRoot] = pRoot;
sz[pRoot] += sz[qRoot];
}
}
}
并查集版本4:基于rank进行优化
即在每一个节点上记录这个节点为根的对应树它的最大深度是多少,在合并时候应使用深度比较低的树指向深度比较高的树。
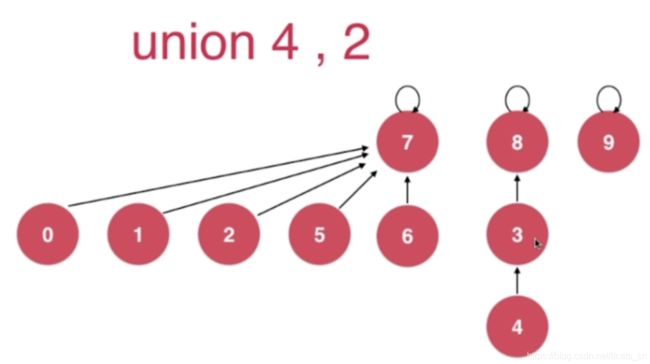
图中我们需要union(4,2),如果我们使用版本3:基于size进行优化的话,节点4所在的树节点总数为3个,节点2所在树节点总数为6个,即将节点个数少的树根节点8指向节点较多的树根节点7,如图:
合并之后树的最大深度由3增加为了4,更加合理的方案是让根节点7指向根节点8,即深度低的树指向深度高的树,如图:
树的最大深度仍然为3,这样的优化称为基于rank的优化,使用rank[i]表示根节点为i的树的高度。
package cn.itcats.unionFind;
public class UnionFind4 implements UnionFind{
//创建一个id数组
private int [] parent;
//新增一个数组
private int[] rank; //表示以i为根的集合中元素的深度
public UnionFind4(int size){
rank = new int[size]; //对sz进行初始化
parent = new int[size];
for(int i = 0 ; i < parent.length ; i++) {
parent[i] = i;
rank[i] = 1;
}
}
public int getSize() {
return parent.length;
}
//查找元素p所对应的集合编号
//O(h)复杂度,h为树的高度
private int find(int p){
if(p < 0 && p >= parent.length)
throw new IllegalArgumentException("p is out of bound");
while(p != parent[p])
p = parent[p];
return p;
}
//查询元素p或元素p是否属于同一个集合
//O(h)复杂度,h为树的高度
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
//根据两个元素所在树的rank不同判断合并方向
//将rank比较低的集合合并到rank高的集合上
public void unionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot)
return;
if(rank[pRoot] < rank[qRoot]){
parent[pRoot] = qRoot;
}else if(rank[qRoot] < rank[pRoot]){
parent[qRoot] = pRoot;
}else{
parent[pRoot] = qRoot;
rank[qRoot] += 1;
}
}
}
三、路径压缩
图示的三棵树实际上都是等效的,他们都相互连接,但它们深度不同,对应的查询效率也不同。
之前我们在对树进行union操作的时候,都是将某个树的根节点指向另外一个树的根节点,在操作数量大的情况下,就难免造成树的深度过大。所谓的路径压缩所解决的问题就是将一个比较高的树压缩称为矮的树。对于并查集而言,每一个树的子树个数并没有限制,理想情况下我们希望我们的树是上图所示中间那个形状【即只有两层,根节点在第一层,子节点在第二层】
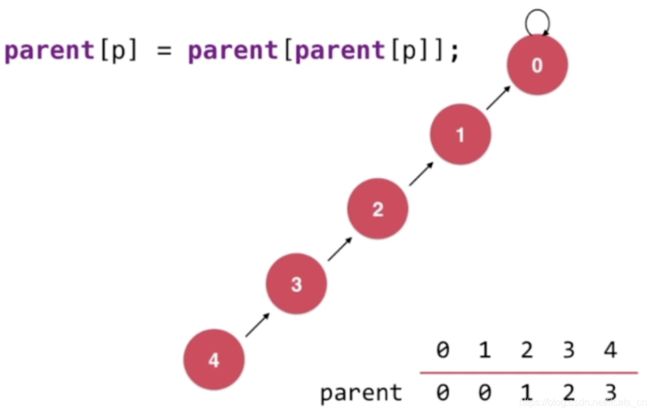
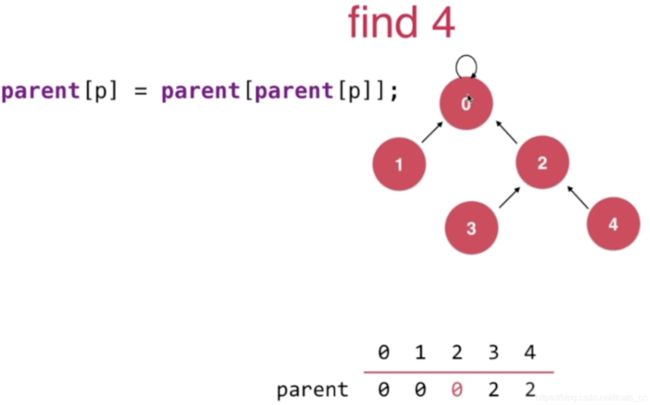
如我们进行find(4)操作,需要经过4次寻址,树的高度为5,即:
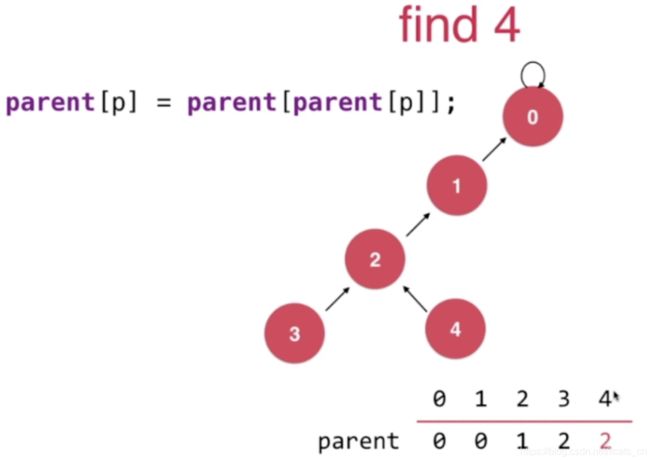
当我们向上遍历的时候执行 parent[p] = parent[parent[p]],即将节点p的父节点设置为节点p父亲节点的父亲节点。
此时0已经是根节点无需继续向上查找了。整棵树从原来的深度为5降到了深度为3,也就是我们在查询节点4的根节点时候,把树的结构也改变了。在version4基础上,只需要修改find()方法即可具体的编码实现:
//新增路径压缩的过程
private int find(int p){
if(p < 0 && p >= parent.length)
throw new IllegalArgumentException("p is out of bound");
while(p != parent[p]) {
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
基于路径压缩版本6
如果我们想将路径压缩为下图形状,需要借助递归实现:
同样,只需要在version4的基础上,修改find()方法即可
//新增路径压缩的过程
private int find(int p){
if(p < 0 && p >= parent.length)
throw new IllegalArgumentException("p is out of bound");
if(p != parent[p])
parent[p] = find(parent[p]);
return parent[p];
}经过性能测试发现还是version5性能最好,因为递归调用本身就是有性能开销的。
四、压缩后的并查集时间复杂度分析
O(1) < O(log*n) < O(logn)