高精度算法:做一个支持正负、小数高精度运算的C++类
一、算法理论
1.概述
2.储存大数字
3.1乘法运算
3.2加法运算
3.3减法运算
3.4除法运算
二、类的构思
三、完整代码
四、拓展想法
一、算法理论
(第一部分旨在说明思路,完整的代码会在第三部分给出)
1. 概述
基本数据类型无法对过大的数据进行精确存取与运算,所以我们需要用高精度算法来对这些大数字进行运算。高精度算法需要考虑两个问题:①如何存储 ②如何运算。
先对于后者,我们可以选择竖式运算,这可以把大数字的运算转换成若干步小数字运算;
所以相应的,对于前者,我们需要选择一种适合竖式运算的存储方式——数组。竖式运算按数位运算,而数组可以把大数字按数组存储。
2.1储存大数字:正整数
用数组存储数字的方式我建议以具体运算而改变。因为某些运算的运算的开始点不同。
比如加法,是从最低位开始加的(如在竖式中,200+4是先个位的0和4相加);
而除法,是从最高位开始除的(如200/25是25先尝试和最百位的2相除,不够除再向十位借位除……)
但存储是为了运算的,所以应该选择方便运算的方式。
举个例子:
int a[101];
如果我要储存12345,且我要进行加法,那么我存储在数组里面就应该是(这里a[0]为了方便而忽略):
| a[1] | a[2] | a[3] | a[4] | a[5] |
|---|---|---|---|---|
| 5 | 4 | 3 | 2 | 1 |
| 个 | 十 | 百 | 千 | 万 |
这样做可以方便相加后对高位进行进位
而如果我要进行除法,那么就应是:
| a[1] | a[2] | a[3] | a[4] | a[5] |
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 |
| 万 | 千 | 百 | 十 | 个 |
这样做可以方便相除后对低位借位或求商
然而这么做问题又来了,一个数组可能存储的是顺序或者倒序数字,那么我怎么知道我存储的是12345还是54321?因此我们还需要一个字符串来以字符形式把数字存储起来,在需要运算时再把它以恰当的规则转换至数组,而且这个字符串应该先用某些方法排除前导0和后导0(也只是为了方便,或者你有更好的储存方式也是可以的)。如果我们想存储012345,则应该想办法把最前面的0去掉,再赋值给字符串:
#include 2.2存储大数字:小数及负数
小数与负数会产生一些特殊符号,无法存储至数组中,那是否也应该存储至字符值中呢?
我的建议是不要(因为我试过,这样会极大地增加字符串处理的难度),而是新建两个变量,一个存储正负号,一个存储小数的长度,而字符值只存储“纯数字”(去除所有符号,所有前导0后导0的值)
举个例子:
我要存储-123.45,那么就应该:
int sign = -1;//正负
int decimal = 2;//小数位
string numString = "12345";//纯数字
2.3存储大数字:字符纯数字补充说明
(这只是我使用的一种储存方式,如果有更好的想法可自行改良)
numString中储存的应该是无符号除前导0后导0值,但保留小数位的所有有效0
下面一组例子能更清晰地读懂这句话:
| 数字 | numString值 |
|---|---|
| 2 | 2 |
| 02 | 2 |
| 2.0 | 2 |
| 0.2 | 2 |
| -2 | 2 |
| -2.3 | 23 |
| 0.002 | 002(保留两个有效0) |
0.002写成002可以使字符串输出时简单一些,但是会导致运算的时候(特别是除法)比较复杂
2.4储存大数字:总结
所以我们需要一些数组容器用于运算,一些变量示意正负与小数,一个字符串存储数字的纯数字字符值
当然如果我们需要输出完整的数字还需要一个额外的函数来组装数字为字符串
为方便运算起见这里还多储存了几个新的变量
#include 3.1.1运算:乘法:数组容器处理
和加法一样,乘法从低位开始相乘,所以应该倒序存放于数组运算容器中。
3.1.2运算:乘法:正负号处理
乘法的正负号好办,直接用两个因数的符号相乘就好了
3.1.3运算:乘法:小数处理
- 运算:无需处理
- 结果:乘法的小数也好办,直接用两个因数的小数相加再排除后导0就好了
3.1.4运算:乘法:纯数字处理
模拟乘法竖式,每位进行相乘,但结果应该存储在哪一位?其实不难找到规律,
个位x个位=个位;
个位x十位=十位;
十位x十位=百位;
所以第i位与第j位相乘,结果将存储于第i+j-1位
另外还需考虑到进位问题,如果出现进位,将增加i+j位的结果值,而i+j-1位只存其与10求余的余数。
举个例子:
18x8=144
先是个位x个位,结果在个位;出现进位,十位要进6,而个位要保留个位结果与10取余的结果4。
再是个位x十位,结果在十位;由于刚刚十位已经有6,十位也溢出需要进位,百位进位至1,十位保留与10取余的结果4
| 百 | 十 | 个 |
|---|---|---|
| 1 | 8 | |
| 8 | ||
| 1(进位1) | 4(进位6+1x8)%10=4) | 4(8x8%10=4) |
运算次数:遍历完每个因数
实现为代码则如下:
//length1和length2是两个因数的长度
for (int secondDigit = 1; secondDigit <= length1; secondDigit++)//遍历到竖式的第二个数
{
for (int firstDigit = 1; firstDigit <= length2; firstDigit++)//遍历到竖式的第一个数
{
//模拟竖式中的某两位数相乘
digitsR[firstDigit + secondDigit - 1] += digits1[firstDigit] * digits2[secondDigit];
//处理进位
digitsR[firstDigit + secondDigit] += digitsR[firstDigit + secondDigit - 1] / 10;
digitsR[firstDigit + secondDigit - 1] = digitsR[firstDigit + secondDigit - 1] % 10;
}
}
值得注意的是那两个+=很关键,不要漏掉了+!
3.2.1运算:加法:数组容器处理
加法从低位开始相加,所以应该倒序存放于数组运算容器中。
3.2.2运算:加法:正负号判断与处理
- 加数同号:可以使用加法竖式进行相加,结果与加数同号
- 加数异号:交给减法处理或再写一次减法的逻辑(详见减法部分,实现方法类似)
3.2.3运算:加法:小数处理
- 运算:需要在存入运算容器前对齐,比如12.3+4,2应该与4对齐
| 十 | 个 | 十分 |
|---|---|---|
| 1 | 2 | 3 |
| 4 | 0 |
换句话说,存储在数组里面的应该是321和04
| digits1[1] | digits1[2] | digits1[3] |
|---|---|---|
| 3 | 2 | 1 |
| 十分 | 个 | 十 |
| digits2[1] | digits2[2] | digits2[3] |
|---|---|---|
| 0 | 4 | 0 |
| 十分 | 个 | 十 |
- 结果:小数先取两个加数中较长的,再排除后导0
3.2.4运算:加法:纯数字处理(仅同号相加,异号参考减法思路)
i位相加存于结果i位中,若要进位则i+1位结果+1,i位结果与10取余
运算次数LoopTime = 两个加数的较长整数位+较长小数位
for (int i = 1; i <= loopTime; i++)
{
digitsR[i] += digits1[i] + digits2[i];
digitsR[i + 1] += digitsR[i] / 10;
digitsR[i] = digitsR[i] % 10;
}
3.3.1运算:减法:数组容器处理
减法从低位开始相减,所以应该倒序存放于数组运算容器中。
3.3.2运算:减法:正负号判断与处理
- 同号:大减小,结果符号结合减数大小判断
被减数大:结果符号与减数一致
减数大:结果符号与减数(或被减数)相反 - 异号:交给加法处理或再写一次加法逻辑
3.3.3运算:减法:小数处理
(同加法一样,详见加法的小数处理)
- 运算:需要对齐
- 结果:取减数与被减数较大者,再排除后导0
3.3.4运算:减法:数字比较
减法竖式需要选出较大的数,比如5-7=-2,应该是较大的7减去5,再修正结果符号为负
由于我们使用字符串类来存储“纯数字”,所以比较的代码比较简短
//integer1和integer2为两个数的整数位
//numString是两个string类字符串
if (integer1 > integer2)
return 1;
else if (integer1 < integer2)
return -1;
else if (numString1 > numString2)
return 1;
else if (numString1 == numString2)
return 0;
else
return -1;
3.3.5运算:减法:纯数字处理(仅同号相减,异号参考加法思路)
第i位相减,借位时需要向被减数借位,此时第i位+10,而第i+1位的减数-1
运算次数LoopTime = 两个加数的较长整数位+较长小数位
注意:这里要确保digits1存的数一定比digits2要大,这点可配合上一步实现
for (int i = 1; i <= loopTime; i++)
{
//digits1的值一定要比digits2要大!!!
if (digits1[i] + digitsR[i] >= digits2[i])//在可能的借位后还够不够减?
digitsR[i] += digits1[i] - digits2[i];
else
{
digitsR[i + 1]--;
digitsR[i] += 10 + digits1[i] - digits2[i];
}
}
3.4.1运算:除法:数组容器处理
除数和被除数的处理和以上的不同,应该以顺序存放于数组(详见2.1)
3.4.2运算:除法:正负号处理
两符号相乘即可
3.4.3运算:除法:小数处理
- 运算:如除数为0.02这种,要想办法跳过多余的0,只把2录到运算数组中,否则会影响后面的试商
- 结果:注意除数的小数也会导致结果小数位改变
3.4.4.1运算:除法:纯数字处理:简述
高精度除法是用减法模拟乘法试商,比如10/2=5,我们在列竖式的时候会用1~9乘2去试商,从而得出某数位的商。然而在计算机进行乘法试商计算量并不少,而且会用到多次高精度除法,所以我们可以选择用减法来代替乘法。
举个例子:对于10/2(可能需要联想一下除法竖式进行的过程)
1先与2对齐,由于不够减,于是除数移动到下一位
0就与2对齐,由于此时有十位的借位1,于是可以进行相减,被除数由10变为8,个位商+1=1
8就与2对齐,可以相减,被除数由8变6,个位商+1=2
……
不够减就执行到下一位
直到执行到除数运算容器的末尾为止
3.4.4.2运算:除法:纯数字处理:引入标记变量(这步只是为了方便说明后面的步骤)
为了减法试商,我们需要准确地获取当前是哪个数位在进行试商。为了方便起见这里对处理除法的函数再引入三个变量
int checkPointFront = 1;//当前试商时被除数的最前检查点(用于减法试商前比较的标记)
int checkPointTrail = 除数的长度;//当前试商时被除数的最后检查点(用于相减的标记)
int divisorcheckTrail = 除数的长度;//记录试商时除数的最后检查点(用于相减的标记)
比如三个变量记录的位置依次如图所示:
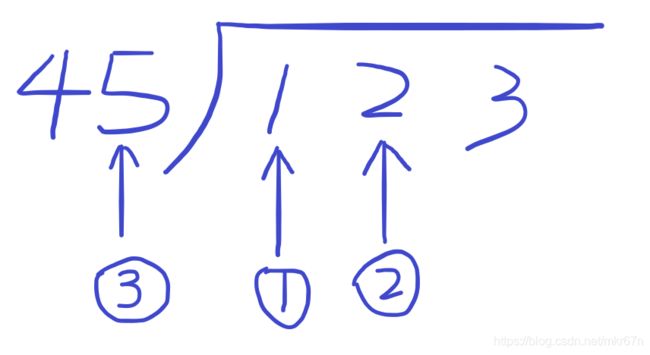
其中①和②每轮试商完毕之后都会向后跳一位
具体作用会在后面两步体现
3.4.4.3运算:除法:纯数字处理:试商比较
怎么才能知道当前数位的试商已经结束(被除数当前位不够减了)?显然我们又需要进行判断,并且每减一次之前都要执行这个判断
这是一个被除数的局部数字和除数进行比较,显然之前减法提及的数字比较不适用
//先假定可以减
bool canSub = true;
//判断是否能够进行减法试商(够不够减)
if (digits1[checkPointFront - 1] == 0)//如果没有借位才判断,否则直接跳出
{
//看看够不够减
for (int i = checkPointFront, j = 1; i <= checkPointTrail; i++, j++)
{
//如果大于,则肯定够减,直接跳出
if (digits1[i] > digits2[j])
{
break;
}
//如果执行到这一句,唯一的情况就是前若干位都等于,且这一位小于,因此整体值为小于,不能减
if (digits1[i] < digits2[j])
{
canSub = false;
break;
}
}
}
最后可以得到一个准确的判断结果
3.4.4.4运算:除法:纯数字处理:减法试商
整体思路:
//遍历到运算数组结束为止
//checkPointTrail恰好也指向当前试商结果的位置
//checkPointFront, checkPointTrail都要在每次循环结束后往后跳一
for (checkPointTrail; checkPointTrail <= 100; checkPointFront++, checkPointTrail++)
{
while (1)
{
这里插入上面的比较代码,得到一个canSub值
if (canSub)
{
进行减法试商,相减后该位的商+1
具体代码详见下面
}
else
{
break;//跳出循环,代表试商结束
}
}
}
减法试商具体代码:
for (int i = checkPointTrail, j = divisorcheckTrail; j > 0; i--, j--)
{
//如果直接能减那就减
if (digits1[i] >= digits2[j])
digits1[i] -= digits2[j];
else
{
//否则进行借位减法
digits1[i - 1]--;
digits1[i] = 10 + digits1[i] - digits2[j];
}
}
digitsR[checkPointTrail]++;//商++ 这是我们最终的目标
当大循环执行完毕后,就可以得到商的完整的结果
而此时digits1会变成全为0的数组,所以这个除法运算是会改变原数组的,这也是为什么要把数字值存储在string中,而不存在数组中的原因之一
二、类的构思
首先定义一个Number类
class Number{//包含以下的成员...};
需要使用字符串类
#include 需要使用变量来记录大数字
int sign = 1;
int length = 0;
int integer = 0;
int decimal = 0;
string numString;//储存无符号的数字(同时去除前导0和后导0,但保留小数位的有效0)
需要有3个运算容器用于二元运算及结果
考虑到所有类共用3个容器,且容器需要在第一次使用时初始化为0,这里定义为static变量
容器的大小决定了最大运算范围,这里101代表最多可进行约50位数×50位数的乘法运算
static int digits1[101];
static int digits2[101];
static int digitsR[101];
//注意static成员在类外需要再定义一次
需要有录入数字的构造函数,考虑到实际使用,这里定义了多个构造函数
函数的具体代码参考后面的完整代码
Number(const string& inputString){//...}
Number(const int& inputNumber){//...}
Number(const long long int& inputNumber){//...}
//这个函数的实现精度只有大概6位,太长的浮点数应用字符串录入
Number(const double& inputNumber){//...}
//用于运算结果的Number对象构造,包含对-0的修正
Number(int resultSign, int resultLength, int resultInteger, int resultDecimal, string resultString){//...}
需要获得完整数字(字符串)的函数
函数的具体代码参考后面的完整代码
string GetFullNumber(){//...}
需要有Number类的四则运算符重载
函数的具体代码参考后面的完整代码
Number operator + (const Number& addend){//...}
Number operator - (const Number& subtractor){//...}
Number operator * (const Number& factor){//...}
Number operator / (const Number& divisor){//...}
需要有若干个类内部运算所需的private函数
三、完整代码
(运算符重载中部分又长又臭的代码可能在第一部分有解释到)
#include 这里再给出2个测试用函数
//字符输入测试
void textCheck()
{
while (1)
{
char ch[100];
cout << "请输入一个数字";
cin >> ch;
Number number(ch);
cout << "numString存储字符值为"<< number.numString << endl;
string copy = number.GetFullNumber();
cout << "获取数字函数输出字符值为" << copy << endl;
}
}
//运算测试,可以把倒数第二行的+改成-*/,即可测试其它三个运算
void additionCheck()
{
while (1)
{
char ch1[100];
char ch2[100];
cout << endl << "请输入第一个数字" << endl;
cin >> ch1;
cout << endl << "请输入第二个数字" << endl;
cin >> ch2;
Number a(ch1);
Number b(ch2);
Number c = a + b;
cout << c.GetFullNumber() << endl;
}
}
四、拓展想法
- BUG修复:其实这个类应该还会有我没发现的bug
(因为字符串与数组的相互转换带来了太多细节操作= =) - 考虑加入开根等更多运算
(可以直接用现有的公式,比如牛顿法,都是基于四则运算的) - 可以加入字符串的录入检测,当输入不正确的字符串时应该有相应处理
- 加入Number类到标准类型的转换,以便必要时数据交互