曼德博集合|最直观的数学之美——用Python看到“上帝的指纹”

1. 关于曼德博集合的简单介绍：

曼德博集合（Mandelbrot set，或译为曼德布洛特复数集合）是一种在复平面上组成分形的点的集合，以数学家本华·曼德博的名字命名。曼德博集合与朱利亚集合有些相似的地方，例如使用相同的复二次多项式来进行迭代。
将曼德博集合无限放大都能够有精妙的细节在内，而这瑰丽的图案仅仅由一个简单的公式生成。因此有人认为曼德博集合是“人类有史以来做出的最奇异、最瑰丽的几何图形”，曾被称为“上帝的指纹”。

---

这是引自百度百科的一段介绍。总而言之，曼德博集合的发现使我们能以最直观的方式看到所谓的“数学之美”。

---

2. 如何获得曼德博集合：

从上一段介绍中，我们知道首先曼德博集合是定义在复平面上的。实际上关于复数概念，我们可以把它看作一种将(x,y)两个变量用一个复变量z代替的简单写法，无需顾虑太多。其次，曼德博集合是通过一个迭代方程以及一些分类规则获得的点的集合，我们来考虑这些问题。

曼德博集合使用到的简单的迭代方程如下：

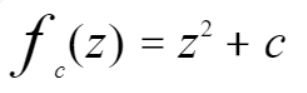
其中，z是复数变量，c是一个复数常量，而非我们通常见到的实数常量。
我们从z = 0开始对这个函数进行迭代，即

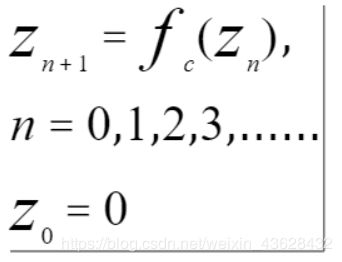
上面这个迭代公式最终可能趋近于无穷大，也可能趋近于某一个收敛值，这取决于复数常量c。所以，我们将所有可以产生收敛值的c归为一类，用某种颜色的点把它们都绘制出来，另一类产生无限大的c则用另一种颜色绘制。通过这几个简单的步骤，我们就能得到“上帝的指纹”——曼德博集合。

借助于计算机，我们将尝试进行这一过程。

---

3. 一些基础知识：

由于曼德博集合需要进行迭代，如果我们使用简单的方法进行计算的话（可能要用到许多层循环），既存在运行时间过长的问题，而且绘制的图形通常比较粗糙。为了快速获得漂亮的图形，我们将使用到NumPy来对计算过程进行矢量化，也就是在计算过程中加入矩阵表示。

下面介绍一些在编程方面的有用知识以及一些数学内容。

---

(1). 绘图必备——函数meshgrid()：

在使用matplotlib进行绘图时，需要传入x和y的坐标值，而通常情况下我们使用向量来进行（也就是使用列表），比如说

import matplotlib.pyplot as plt

plt.figure()
plt.plot([1,2,3],[1,2,3],marker='.',linestyle='')
plt.show()

通过设置参数，我们将得到三个散点，如图：

但是，我们的画布是二维的，如果能使用二维数组传递坐标值，我们将方便的多。matplotlib也为我们提供了支持：

import matplotlib.pyplot as plt

plt.figure()
plt.plot([[1,2,3],[1,2,3],[1,2,3]],[[1,1,1],[2,2,2],[3,3,3]],marker='.',linestyle='')
plt.show()

通过具有平面结构的二维数组，我们更加直观的绘制了这些点：

在上面的例子中，传递坐标值时，我们使用的是矩阵而不是简单的列表。

这样的二维矩阵，我们把它称为坐标矩阵，而meshgrid()就是在需要绘制大量点，而这些点的平面位置有一点规律（比如网格点）时用来帮助我们生成这样的坐标矩阵的。

我们通过使用这个函数绘制上一幅图，来看看这个函数的用法：

import matplotlib.pyplot as plt
import numpy as np

plt.figure()
X,Y = np.meshgrid([1,2,3],[1,2,3])
plt.plot(X,Y,marker='.',linestyle='')
plt.show()

print(X)
print(Y)

绘制的图片和上一幅图相同：

产生的网格状的坐标矩阵也是我们希望的：

[[1 2 3]
 [1 2 3]
 [1 2 3]]
[[1 1 1]
 [2 2 2]
 [3 3 3]]

这种方法远比使用列表快速、方便的多。

---

(2). 小技巧：数组的逻辑索引

为了既能绘制优美的曼德博集合，又能免去考虑复杂的colormap参数，我们将使用数组的逻辑索引作为简化问题的小技巧。

下面我们来介绍一个数组如何使用逻辑数组来进行索引：

import numpy as np

arr = np.array([1,2,3,4,5])
index = np.array([True,False,True,False,True])
print(arr[index])

上面的代码创建了两个相同形状的数组，其中一个是逻辑数组。使用逻辑数组作为数组的索引，我们看到结果是

[1 3 5]

也就是只返回了布尔值为True的位置的值。

下面我们看看二维数组的情况：

import matplotlib.pyplot as plt
import numpy as np

arr = np.array([[1,2,3],[4,5,6],[7,8,9]])
bool_index = np.array([[True,True,True],[True,False,True],[True,True,True]])
print(arr[bool_index])

结果是

[1 2 3 4 6 7 8 9]

也就是说，即使是二维数组，经过逻辑索引之后也只能得到一维的向量。

这种方式看起来似乎用处不大，但是看下面的代码：

arr[bool_index] = 100
print(arr)

这样做的结果是

[[100 100 100]
 [100   5 100]
 [100 100 100]]

也就是说，我们使用这种索引方式进行赋值操作时，数组将只改变逻辑数组为True位置的数组值，而数组的形状与其它的值都不会变化。

(3). 大大简化工作——两条数学定理：

在百度百科的【曼德博集合】词条中我们可以发现两条十分有用的定理：

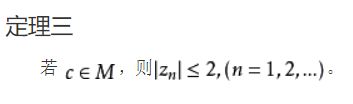
定理二告诉我们，如果我们的坐标点在曼德博集合中，那么它将被包含在一个半径为2的圆内，如果我们简化一点的话，我们可以说：我们想要的图形坐标范围将在（-2，2）以及（-2，2）之间，这为我们确定了一个很准确的范围。

定理三告诉我们，如果某一次迭代中z的值超过了2，那么我们就可以结束了——因为这时我们就确定了这个点不属于曼德博集合。所以，我们不需要以迭代一定次数之后值是否为无穷大作为分类依据了——无穷大这个值包含太多不确定。我们只需要使用小小的、可爱的2作为无穷大的替代。

我们真应该感谢百度百科，唯一的遗憾是它没有给出证明。

这里我们不想证明它们，或许以后我们会做做尝试。

---

上面这三点将帮助我们理解代码并绘制出我们想要的曼德博集合。下面我们将直接给出代码，如果你能读懂上面的全部内容的话，阅读下面代码将很简单。

4. 所有的代码：

import numpy as np
import matplotlib.pyplot as plt

def my_meshgrid(width,step):
	'产生用于复变量c的X、Y网格矩阵。'

	x = np.linspace(-width,width,step)
	y = np.linspace(-width,width,step)

	X,Y = np.meshgrid(x,y)

	xmax,xmin,ymax,ymin = x.max(),x.min(),y.max(),y.min()

	return (X,Y),(xmax,xmin,ymax,ymin)

def draw_mandelberg_set(X,Y):
	'根据传入的网格矩阵生成一个用于可视化的矩阵。'

	c = np.array(X + 1j*Y,dtype=complex)
	z = np.zeros(c.shape,dtype=complex)

	bool_index = np.ones(c.shape,dtype=bool)
	matrix_map = np.ones(c.shape)

	for i in range(50):
		z[bool_index] = pow(z[bool_index],2) + c[bool_index]

		bool_index = (np.abs(z) < 2)
		matrix_map += bool_index

	return matrix_map

def main(width=2,step=1000):
	'主函数'

	plt.figure()
	plt.axis('off')

	(X,Y),extent = my_meshgrid(width,step)

	matrix_map = draw_mandelberg_set(X,Y)
	
	plt.imshow(matrix_map,extent=extent,cmap=plt.cm.hot)

	plt.show()

5. “上帝的指纹”——最终结果

简单的运行一遍主函数，我们即可获得“上帝的指纹”——曼德博集合：

为了一窥“上帝的指纹”更美的细节，我们对一些函数做一些修改，使我们能更灵活的通过调整X与Y的范围看到我们希望的细节，同时，我们会将图片写入文件中，用大量的图片满足我们对数学之美的渴望。

完整的代码如下：

import numpy as np
import matplotlib.pyplot as plt

def my_meshgrid(rangex,rangey,step):
    '产生用于复变量c的X、Y网格矩阵。'

    x = np.linspace(rangex[0],rangex[1],step)
    y = np.linspace(rangey[0],rangey[1],step)

    X,Y = np.meshgrid(x,y)

    xmax,xmin,ymax,ymin = x.max(),x.min(),y.max(),y.min()

    return (X,Y),(xmax,xmin,ymax,ymin)

def draw_mandelberg_set(X,Y):
    '根据传入的网格矩阵生成一个用于可视化的矩阵。'

    c = np.array(X + 1j*Y,dtype=complex)
    z = np.zeros(c.shape,dtype=complex)

    bool_index = np.ones(c.shape,dtype=bool)
    matrix_map = np.ones(c.shape)

    for i in range(50):
        z[bool_index] = pow(z[bool_index],2) + c[bool_index]

        bool_index = (np.abs(z) < 2)
        matrix_map += bool_index

    return matrix_map

def get_images(rangex=(-2,2),rangey=(-2,2),step=1000):
    '主函数'

    plt.figure()
    plt.axis('off')

    (X,Y),extent = my_meshgrid(rangex,rangey,step)

    matrix_map = draw_mandelberg_set(X,Y)
    
    return plt.imshow(matrix_map,extent=extent,cmap=plt.cm.hot)

def main(start,step,bias):
    
    while start <= 2:

        get_images((start,start+step),(start+bias,start+step+bias))
        plt.savefig('image{}.png'.format(start))
        start += step

下面是我在一段时间内获得几张图片，我们也可以自己运行获得更多（这个过程中将产生大量的黑色图片，使得找到一个曼德博集合的图片很令人兴奋）。在调整参数的时候，我们要记得曼德博集合与分形——这意味着不论我们的参数如何小，我们在那个尺度下的某个位置任然看得到复杂的曼德博集合。

6. 欣赏时间