从A*算法看AI寻路问题

一.寻路问题

寻路问题一直以来都是十分经典和有趣的问题，在我们生活中以及人工智能方面有着及其重要的研究价值。简而言之，寻路问题就是在给定起点和终点的情况下，找出一条可到达的最短路径，一路上可能有墙，坑，湖等不可经过的地段。

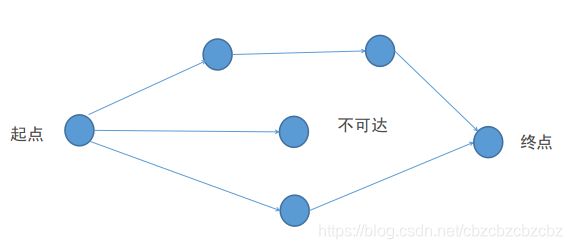
表现在数据结构里面就是一张图，如下所示。

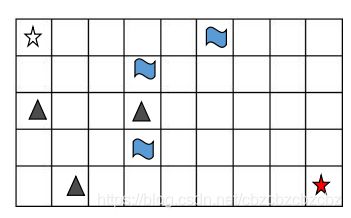
我们可以对模型进行一下简化，便于我们分析问题。我们将寻路问题简化成一张方格表，类似于棋盘一样：

 

 

图中，空五角星为起点，红五角星为终点，图上有河流，山峰等无法穿越的地区，需要从空五角星走到红五角星。

 

 

二.寻路问题的几种解法

寻路问题很古老也很经典，目前比较常见的算法有广度优先，Dijkstra算法，A*算法以及“万能的”遗传算法等等。

 

1.深度优先搜索也是遍历图的一种方法，但是对于求最短路径作用不大。广度优先算法比较适合用来求最短路径，因为它本质上是从起点遍历所有相邻点，继而往外扩散直到找到终点。

   广度优先的基本步骤如下：

   a.将根节点加入队列

   b.从队列取出节点，判断是否是目标节点，是则输出，否则遍历所有相邻节点，并加入队列

   c.如果队列为空，则输出无法找到目标节点

   可以看出来，BFS算法存在盲目搜索的感觉，简单的遍历所有节点而不考虑可能性大的节点。

 

2.遗传算法也可用于寻路问题，之所以说遗传算法是“万能”的，因为只要是演化计算求最优解的案例都可以采用遗传算法。基本步骤如下：

   a.对基因进行编码，每个基因代表一条路径

   b.对基因进行交叉，变异，表现为交换路径某处的格子，或者直接替换某处的格子

   c.选择距离终点最近的路线，即优秀的基因，产生下一代种群

   d.循环往复，直到找出包含终点的路径

   可以看出，遗传算法的通用性决定了它肯定不是最佳解法。种群的数量，筛选的机制等都会影响最终结果，并且会很容易陷入局部最优，从而无法得到全局最优解。

 

3.Dijkstra算法是十分优秀的求单源最短路径的算法，相比于BFS算法，增加了权值的概念，这样我们就能找到到达终点的最短路径，而不仅仅是某条路径而已。基本步骤如下：

   a.每个顶点都有一个代价值，每条边都有一个权值，起点首先加入到路径中

   b.遍历当前顶点的相邻子节点，代价值等于父节点的代价值加上边的权值，若新代价值小于原代价值，则更新加入到路径中

   c.查找代价值最小的顶点，加入到路径中

   d.重复b，c两步，直到访问完所有的节点

  可以看出，Dijkstra算法只考虑了当前顶点到起始点的代价值，而忽略了当前点到终点的距离

 

三. A*算法

A*算法汲取了Dijkstra算法的优点，同时加入了顶点到终点的代价值，使得它在寻路问题中处于至关重要的地位。寻路问题一直是人工智能中的有趣问题，如何选择最短路径以及最短时间将是首要解决的问题。

 

A*算法的基本步骤如下所示：

1.从起点开始，遍历九宫格的其他8格的代价值，其中代价值F等于当前点到起点的距离G加上当前点到终点的距离H，所有顶点加入到开放列表中，父节点都是起点

2.将起点加入关闭列表，选取F值最小的顶点，将其作为中心点继续遍历九宫格，对于关闭列表的点暂时不考虑，新的顶点加入到开放列表中，同时已在开放列表中的点需要更新代价值F，若新的F值较小，则更新当前点的父节点

3.重复以上步骤，直到九宫格包含终点则输出最短路径，若最终开放列表为空，表示没有路径

 

A*算法的关键概念有以下几处：

1.开放列表表示所有待检查的点集合，这些点都有可能成为最短路径中的某个点。关闭列表表示已经检查过的中心点集合。

2.代价值F=G+H，其中G指的是当前点到周围点的直接距离，如直角为1，斜边为1.4，H指的是周围点到终点的距离。H值我们采用的是“曼哈顿”距离，等于周围点到终点的水平距离加上垂直距离，忽略障碍物的存在。可以看出，H值的计算有着启发式搜索的思想，这是Dijkstra算法所没有的。

3.欧氏距离与曼哈顿距离，欧氏距离指的是两个点之间的直线距离

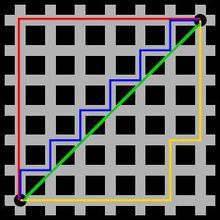
曼哈顿距离指的是两个点之间的水平加垂直距离，下图中绿色表示欧氏距离，红，黄，蓝表示等价的曼哈顿距离(此图来源于网络)

欧氏距离往往伴随着浮点运算，浮点运算相比于整数运算较费时，并且会产生一定的误差，而曼哈顿距离只是简单的加减法，运算起来快速且不会产生误差。

 

 

A*算法图解

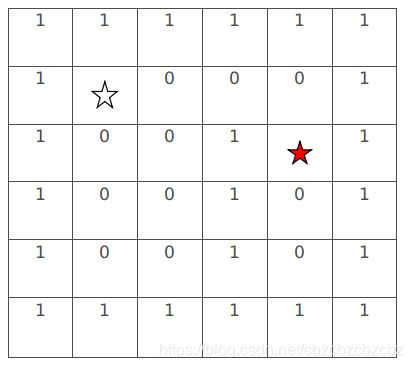
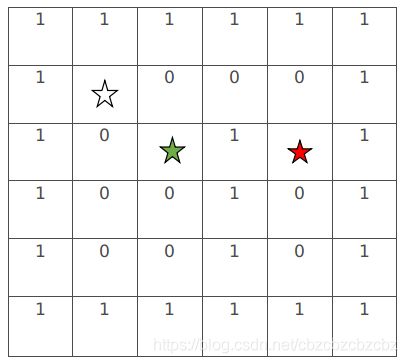
step1：初始状态，空星是起点，红星是终点，0表示可达，1表示不可达

 

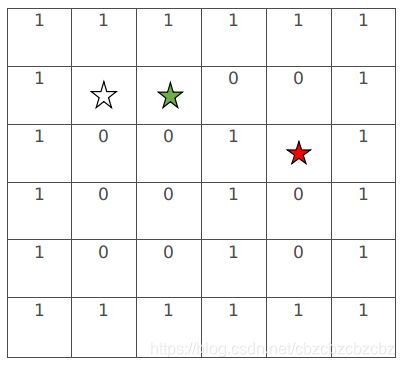
step2：空星点作为当前中心点，检查周围九宫格的点，计算每个点的G值和H值，并加入开放列表，父节点都指向起点。显然，图中绿星是F值最小的，F=1.4+2=3.4，则绿星作为下一轮的中心点，此时空星已加入关闭列表

 

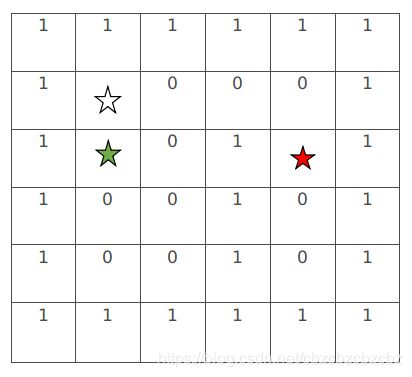
step3：上一步中的绿星同样检查周围九宫格，对于已经在开放列表的点，我们会比较此时的F值和旧的F值，显然，此时还是老的F值最小，F=4，即图中新的绿星位置，绿星再次加入关闭列表

 

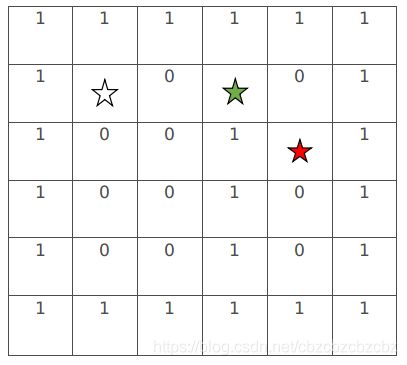
step4：同理，继续检查九宫格，当前中心点变成了下面的绿星，检查原理同上

 

step5：再次从开放列表里面选择F值最低的，此时是下面的绿星

 

 

step6：上一步中的绿星，检查九宫格之后，发现终点就在它的附近，于是直接跑到了终点，程序结束

A*算法的基本思路

1.定义节点信息

class Node  {
    int x;   //点的x坐标
    int y;   //点的y坐标
    Node parent;   //点的父节点
    int F;   //点的代价值F
    int G;   //点距离父节点的距离
    int H;   //点距离终点的距离
 
 
}

2.主要的遍历流程

while (没达到终点)
{
  centerNode=开放列表中最小F值的点
  if (tNode==终点)//tNode表示当前中心点centerNode周围的某个点
  {
     跳出循环,终点指向centerNode;
  }
  while(遍历centerNode的周围点)
    {
        if (tNode==墙，坑，山)//不可达的点
        {
            忽略这个点
        }
        else if(tNode在关闭列表中)
        {
            也无需关注
        }
        else
        {
            tNode.G=centerNode.G+1;//根据tNode相对于centerNode的方向赋予G值，直边取1，斜边取1.4
            tNode.H=getManhattanDistance(tNode,终点);//计算曼哈顿距离
            tNode.F=tNode.G+tNode.H;
            if (开放列表包含tNode)
            {
                检查tNode和已有node的F值,小则更新F值和父节点
            }
            else
            {
                开放列表加入tNode,并指向父节点centerNode
            }
        }
    }
 
    if (开放列表为空或者到达终点)
    {
        跳出while循环
    }
    开放列表移除中心点centerNode,并加入关闭列表
     
}

 

A*算法的运行

上述的伪代码已经比较清楚的介绍了算法思路，我自己写了个demo，算法+UI。个人一直以来都比较喜欢这样做，光写算法不得劲，算法枯燥耗脑，不写个UI来实现一下不舒服。正所谓没有算法的界面是空壳，没有界面的算法不直观，哈哈（其实是我自己说的）。我把运行结果做成了GIF，图中生成了两张地图，一大一小，最外围边上都是墙，中间随机有山峰和湖面，小旗子是终点，大家可以很清楚的看到小人的跑动路径。

 欢迎大家留言，大家一起讨论，一起进步！