2月11日 TensorBoard+DNN+CNN

参考1：http://m.elecfans.com/article/916036.html
参考2：http://www.auto-mooc.com/chapter/study?class_id=6E198952943FF0A4904D4F253B9EC07A&item_id=281AF5DF498C52007E986C0E96FFDDA8
学习资料汇总：暂未提供

修订：深度学习补充2月14 ，深度学习的提出2月17

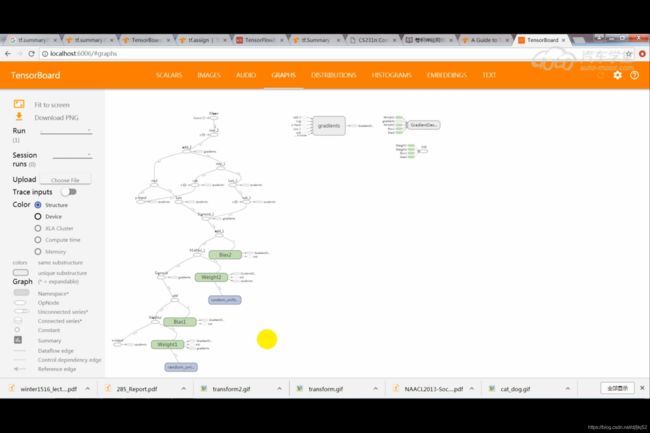
9.4 TensorBoard

Tensor board 是辅助复杂TensorFlow 的可视化工具，就是图的方式来展示整个计算的架构

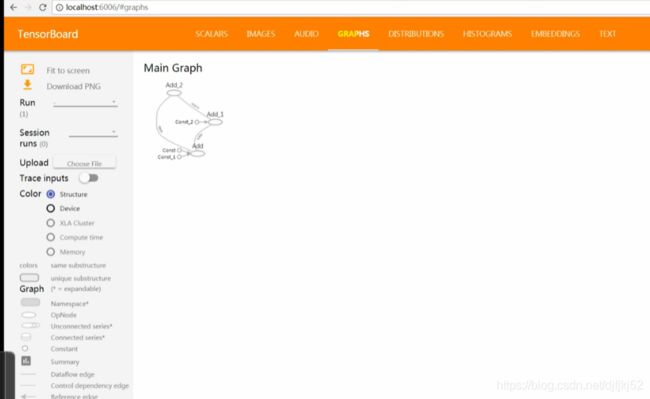
import tensorflow as tf 
a = tf.constant(2) 
b = tf.constant(3) 
x =tf.add(a,b) 

With tf.Session() as sess:              
	print(sess.run(x))

# TensorBoard用法：writer = tf.sumary.FileWriter([logdir], [graph])

writer = tf.summary.FileWriter('./graph/',tf.get_default_graph())

writer.add_graph(s.graph)

writer.close()

tensorboard --logdir=logs --port=6006 ; tensorboard --logdir=./graph --port=8888

9.2 TensorFlow 实例：XOR

tf.reduce_mean 函数用于计算张量tensor沿着指定的数轴（tensor的某一维度）上的的平均值，主要用作降维或者计算tensor（图像）的平均值。

reduce_mean(input_tensor,
                axis=None,
                keep_dims=False,
                name=None,
                reduction_indices=None)
#第一个参数input_tensor： 输入的待降维的tensor;
#第二个参数axis： 指定的轴，如果不指定，则计算所有元素的均值;
#第三个参数keep_dims：是否降维度，设置为True，输出的结果保持输入tensor的形状，设置为False，输出结果会降低维度;
#第四个参数name： 操作的名称;
#第五个参数 reduction_indices：在以前版本中用来指定轴，已弃用;
#————————————————
#原文链接：https://blog.csdn.net/dcrmg/article/details/79797826
#类似函数还有:
#tf.reduce_sum ：计算tensor指定轴方向上的所有元素的累加和;
#tf.reduce_max  :  计算tensor指定轴方向上的各个元素的最大值;
#tf.reduce_all :  计算tensor指定轴方向上的各个元素的逻辑和（and运算）;
#tf.reduce_any:  计算tensor指定轴方向上的各个元素的逻辑或（or运算）;

XOR 代码：

• 首先定义输入,x-input,‘y-input’

import tensorflow as tf

INPUT_X = [[0,0],[0,1],[1,0],[1,1]]
INPUT_Y = [[0],[1],[1],[0]]
#输入占位符
x = tf.placeholder(tf.float32, shape=[4,2], name = 'x-input')
y = tf.placeholder(tf.float32, shape=[4,1], name = 'y-input')

定义权重w，这里面和之前python编程的区别,权重的维度不用加上偏差bias，并另外单独定义偏差：
权重w1是输入层与隐藏层之间的权重，维度[2,2] ;w2是隐藏层与输出层之间的维度[2,1];

#生成随机权重
W1 = tf.Variable(tf.random_uniform([2,2], -1, 1), name = "Weight1")
W2 = tf.Variable(tf.random_uniform([2,1], -1, 1), name = "Weight2")

#每一层的偏差
Bias1 = tf.Variable(tf.zeros([2]), name = "Bias1")
Bias2 = tf.Variable(tf.zeros([1]), name = "Bias2")

然后定义激活函数，cost 代价函数,梯度下降中可以自动求解cost函数的偏导

#Activation 隐藏层的值:使用了激活函数产生的结果A
A = tf.sigmoid(tf.matmul(x, W1) + Bias1)
#所计算出来的输出，Hypothesis
H = tf.sigmoid(tf.matmul(A, W2) + Bias2)

#交叉熵代价函数
cost = tf.reduce_mean(((y * tf.log(H)) +((1 - y) * tf.log(1.0 - H))) * -1)

#梯度下降，反向传播
train_step = tf.train.GradientDescentOptimizer(0.05).minimize(cost)

设置超参数

#初始化参数
init = tf.global_variables_initializer()
with tf.Session() as s:
    s.run(init)
    for i in range(30000):
        s.run(train_step, feed_dict={x: INPUT_X, y: INPUT_Y})
        if i % 1000 == 0:
            print('Hypothesis ', s.run(H, feed_dict={x: INPUT_X, y: INPUT_Y}))
            print('cost ', s.run(cost, feed_dict={x: INPUT_X, y: INPUT_Y}))


writer = tf.summary.FileWriter("./graph", s.graph)

writer.add_graph(s.graph)
writer.close()

10.1DNN深层神经网络

• 计算层数，只计算隐藏层+输出层

感知器：

浅层神经网络：（左图两层；有图三层）

深层神经网络：

分割下列图像

采用多层神经网络，每一层进行操作：

最后：

使用深层神经网络可以减少浅层神经网络所需要的“节点数”。

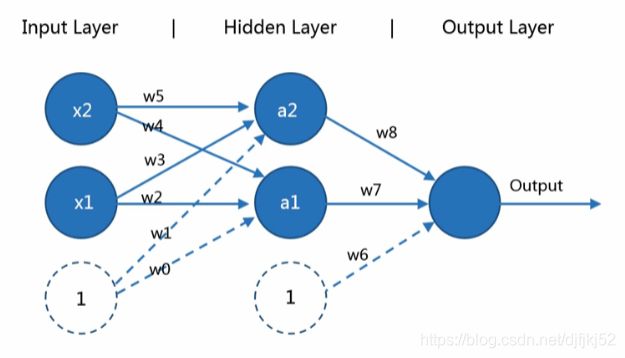
对于只有一个隐藏层的神经网络：

对于下列XOR问题

由数理逻辑可知道：3个元素XOR，2^(3-1)个隐藏层节点。

n个元素输入，进行XOR，2^(n-1)个隐藏层节点。

对DNN来说：

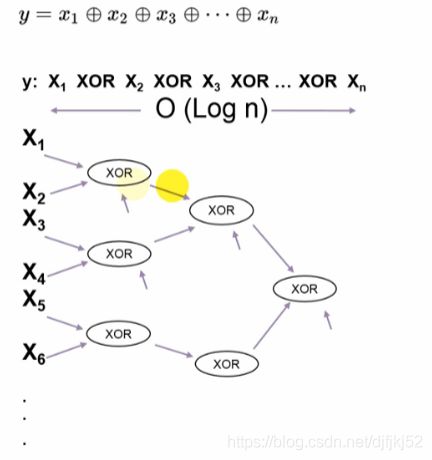
n个元素输入，进行XOR，2(n-1)个隐藏层节点，有O(log N )个层数。

# 权重和偏置；增加一层
# 初始值不能为0；否则无法改变权重
W1 = tf.Variable(tf.truncated_normal([784, 100],  stddev=0.1, dtype=tf.float32))
B1 = tf.Variable(tf.zeros([100]))

W2 = tf.Variable(tf.truncated_normal([100,10], stddev=0.1, dtype=tf.float32))
B2 = tf.Variable(tf.zeros([10]))

#给定输入，计算输出
layer1 = tf.nn.sigmoid(tf.matmul(x, W1) + B1)
H = tf.nn.softmax(tf.matmul(layer1, W2) + B2)

深度学习补充2月14

https://www.cs.toronto.edu/~hinton/

Hinton, G. E. and Salakhutdinov, R. R. (2006)
Reducing the dimensionality of data with neural networks.
Science, Vol. 313. no. 5786, pp. 504 - 507, 28 July 2006.
[ full paper ] [ supporting online material (pdf) ] [ Matlab code ]

可以学习

11.1 CNN

CNN的基本结构包括两层，其一为特征提取层，其二是特征映射层。主要用来识别位移、缩放及其他形式扭曲不变性的二维图形。

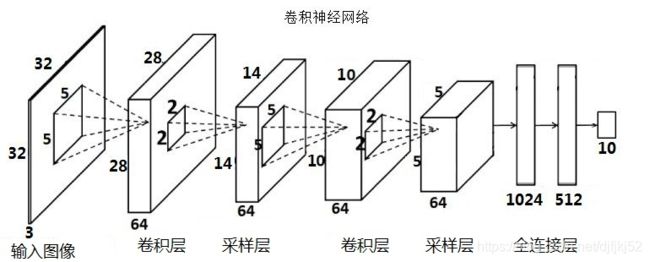
详细参考：https://zhuanlan.zhihu.com/p/33855959

CNN假设了输入就是图像，简化了参数设定与计算。

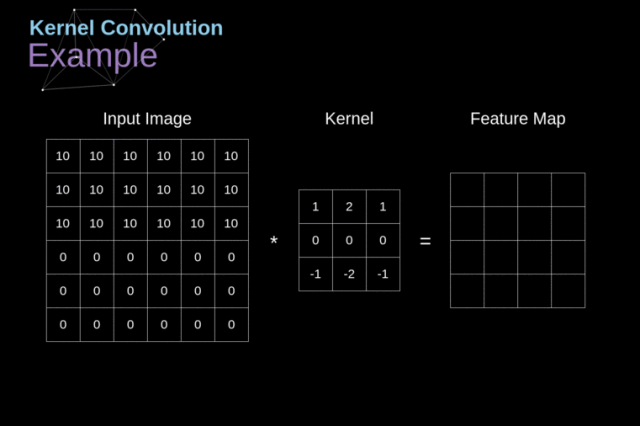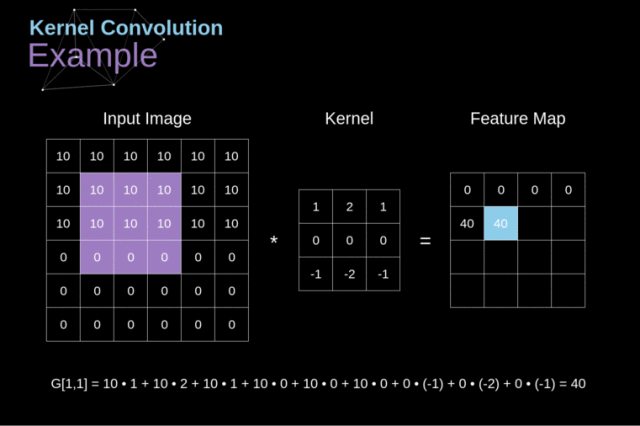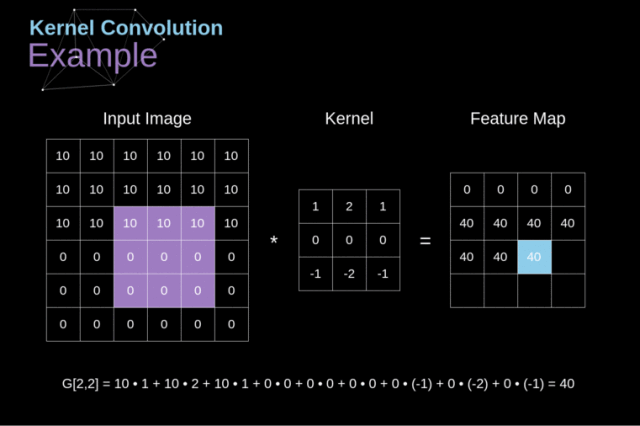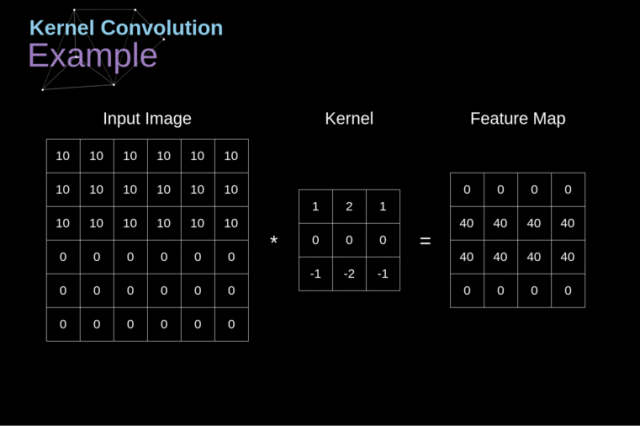
卷积核

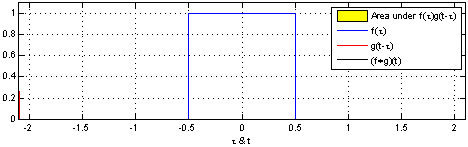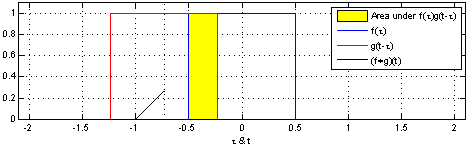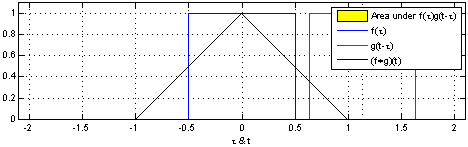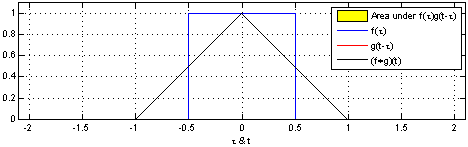
核卷积（kernel convolution）不仅仅用于CNN，它还是许多其他计算机视觉算法的关键要素。核卷积就是将一个小数字矩阵（滤波器，也称作 kernel 或 filter）在图像上进行滑动，并根据 kernel 的值，对图像矩阵的值进行转换的过程。对图像经过卷积操作后得到的输出称为特征映射（feature map）。特征映射的值的计算公式如下，其中 f 代表输入图像，h 代表滤波器 。结果矩阵的行数和列数分别用 m 和 n 表示。

http://m.elecfans.com/article/916036.html

python 中进行卷积计算，卷积核会自动旋转，然后进行计算

input = np.array([[4.0,0,1,0,0], [4,0,3,3,4],[0,1,2,4,4],[3,4,2,4,4],[4,2,1,1,0]])
input = np.matrix(input)
#a = a.transpose()
print(input)

horizontal=np.array([[-1,-2,-1],[0,0,0],[1,2,1]]) #设置水平边缘的卷积核 #核会旋转
print(horizontal)

horizontal_edge3=signal.convolve2d(input,horizontal,boundary='symm',mode='valid') 

tensorflow中的卷积核不会旋转。调用不同接口时，虽然都是进行卷积计算，但是结果却是不同的。

a = np.array([[4.0,0,1,0,0], [4,0,3,3,4],[0,1,2,4,4],[3,4,2,4,4],[4,2,1,1,0]],dtype='float32')
b = a.reshape(1,5,5,1)
#b = b.transpose()
input = tf.constant(b)

c = np.array([[-1.0,-2,-1],[0,0,0],[1,2,1]],dtype='float32')
#c = np.array([[1.0,2,1],[0,0,0],[-1,-2,-1]],dtype='float32')
d = c.reshape(3,3,1,1)
filter = tf.constant(d)

op = tf.nn.conv2d(input, filter, strides=[1, 1, 1, 1], padding='VALID')

下图展示了使用几个不同 kernel 的卷积结果。

问题：

问题：	措施
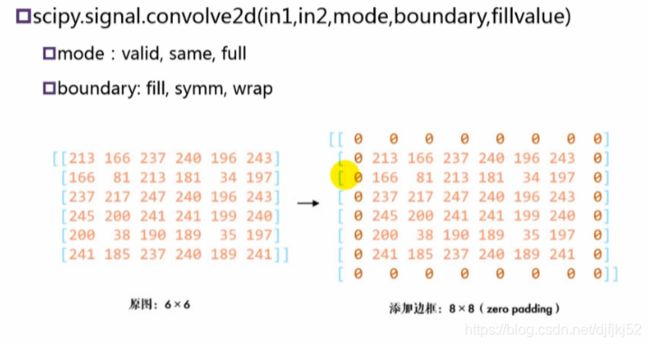
由于每次执行卷积时我们的图像都会缩小，因此在我们的图像完全消失之前，我们只能进行有限次数的卷积。另外，如果对kernel 在图像中移动的过程进行观察，我们就会发现图像外围像素的影响远小于图像中心像素的影响。	为了解决这两个问题，我们可以使用额外的边框来填充图像（padding）。例如，如果使用 1像素进行填充，我们将图像的大小增加到 8x8，因此使用 3x3 的 kernel 的卷积，其输出尺寸将为 6x6 。在实践中，我们通常用零值来填充额外的边界。

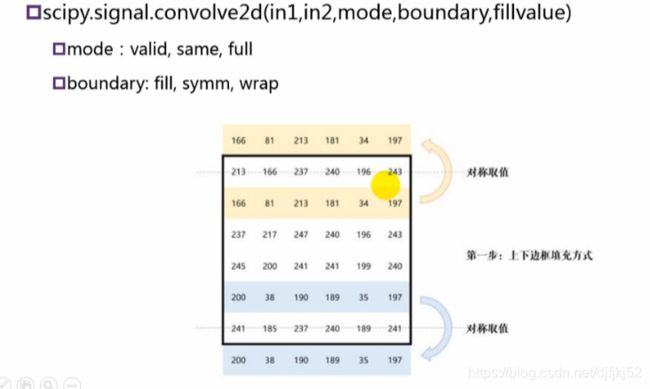
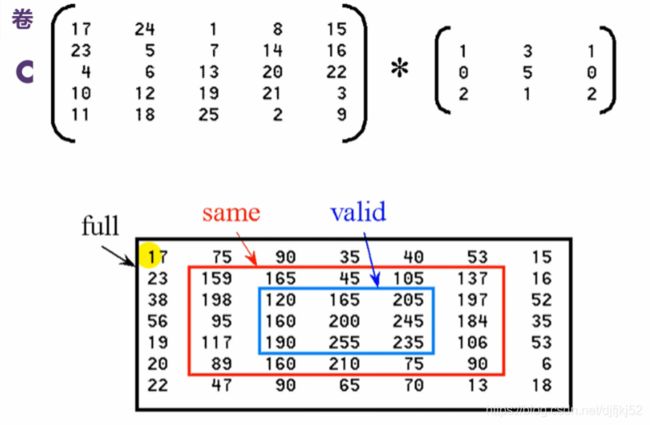
填补填充两种方式

根据是否使用填充，我们将处理两种类型的卷积——Valid 和 Same	有效卷积&相同卷积（Valid and Same Convolution）
Valid——使用原始图像	Same——使用原始图像并使用它周围的边框，以便使输入和输出的图像大小相同。

在Same情况下，填充宽度应满足以下等式，其中 p 是填充尺寸，f 是kernel 尺寸（通常是奇数）。

填充方式1：0填充

填充方式2：对称

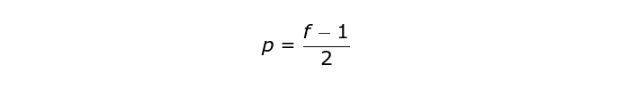
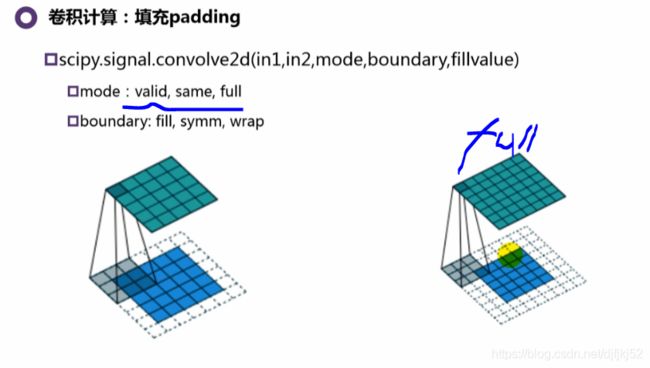
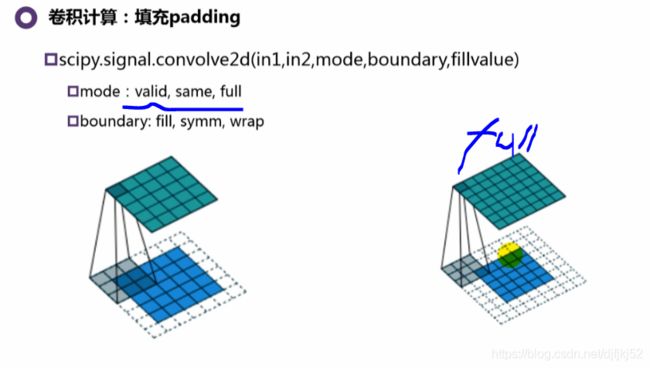
跨步卷积（Strided Convolution）	在设计CNN架构时，如果希望感知域重叠较少，或者希望让特征图的空间维度更小，我们可以增加每次将 kernel 移动几个像素步长。输出矩阵的尺寸（考虑填充和步长时）可以使用以下公式计算。其中：n - 图像大小，f  - 滤波器大小，nc  - 图像中的通道数，p - 填充大小，s -  步幅大小，nf  - kernel 的数量

input = tf.Variable(tf.random_uniform([1, 5, 5, 1],0,5))

filter = tf.Variable(tf.random_normal([3, 3, 1, 1]))

op = tf.nn.conv2d(input, filter, strides=[1, 2, 2, 1], padding='VALID')

体积卷积（Convolution over volume）

• 不仅使能够处理彩色图像，
• 更为重要的是，能够在单层网络中使用多个 kernel

第一个规则是 kernel 和图像必须具有相同数量的通道。一般而言，图像的处理过程是将三维空间中的值对相乘。
如果想在同一个图像上使用多个 kernel，首先我们要分别对每个kernel执行卷积，然后将结果从顶层向下进行叠加，最后将它们组合成一个整体。
输出张量的尺寸（可以称为3D矩阵）满足以下等式，其中：n - 图像大小，f  - 滤波器大小，nc  - 图像中的通道数，p - 填充大小，s -  步幅大小，nf  - kernel 的数量。

CNN图形特征

计算机对于图像识别输出的是三维矩阵：255 X 255 的二维像素，加上第三维深度。

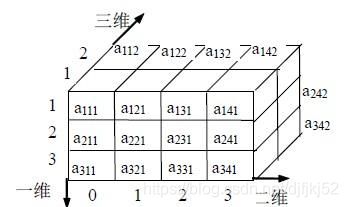
#将RGB图转换为灰度图
def rgb2gray(rgb):
    return np.dot(rgb, [0.299, 0.587, 0.114])#参数是权重

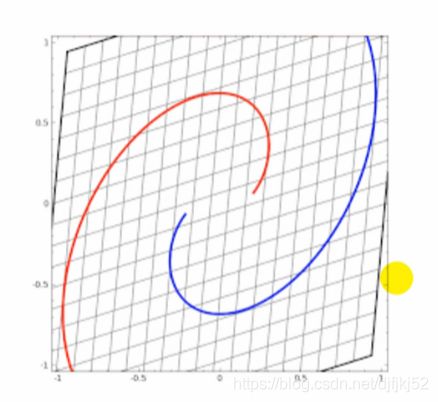
卷积在图像识别的作用：

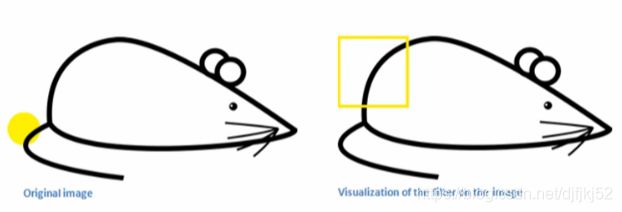
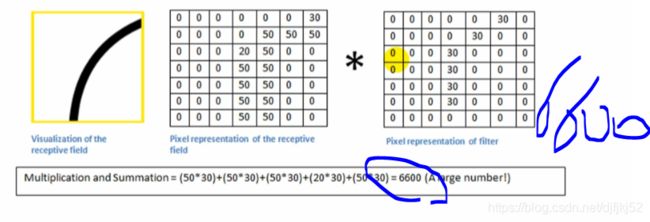
为了能识别黄色框框的曲线，需要定义“卷积核”，如下图就是卷积核

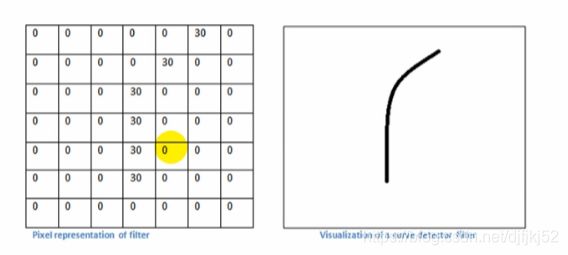
如下图是7x7卷积核矩阵

p = np.array([0,0,0,0,0,30,0,0,0,0,0,30,0,0,0,0,0,30,0,0,0,0,0,0,30,0,0,0,0,0,0,30,0,0,0,0,0,0,30,0,0,0,0,0,0,0,0,0,0])
print(len(p))
m = p.reshape(7,7)

不是卷积核想要的形状就会是“0”。

一开始也不知道有哪些卷积核，在不断的训练后，得到适合的卷积核，卷积核就是CNN的参数。

#将RGBA图转换为灰度图
def rgb2gray(rgb):
    return np.dot(rgb[...,:3], [0.299, 0.587, 0.114])

img = plt.imread("android.png") #结果为[256,256,4],RGBA
#print(img)
#plt.imshow(img)
#转换为灰度图；将图变为二维矩阵；便于与卷积核进行卷积
img = rgb2gray(img)
plt.imshow(img)

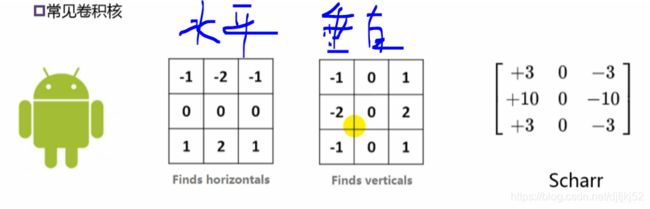
horizontal=np.array([[-1,-2,-1],[0,0,0],[1,2,1]]) #设置水平边缘的卷积核
vertical = np.array([[-1,0,1],[-2,0,2],[-1,0,1]])
scharr = np.array([[3,0,-3],[10,0,-10],[3,0,-3]])
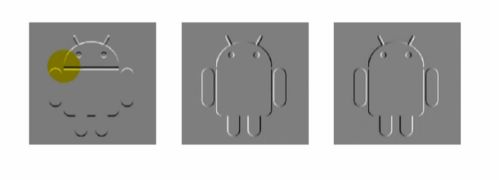
horizontal_edge=signal.convolve2d(img,horizontal,boundary='symm',mode='same') #把图像和水平卷积核作二维卷积运算,设计边界处理方式为symm
vertical_edge=signal.convolve2d(img,vertical,boundary='symm',mode='same') #把图像和设计好的垂直卷积核作二维卷积运算,设计边界处理方式为symm
scharr_edge=signal.convolve2d(img,scharr,boundary='symm',mode='same') #把图像和设计好的垂直卷积核作二维卷积运算,设计边界处理方式为symm
print(horizontal_edge.size)

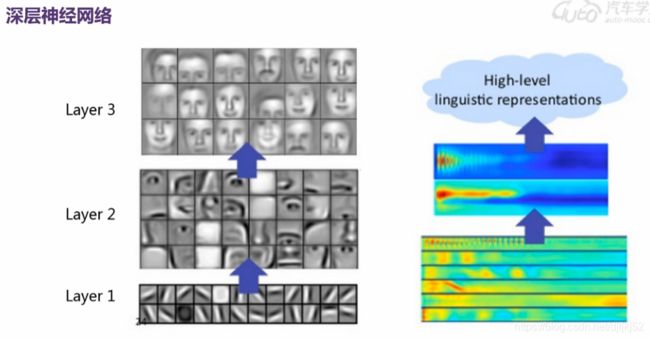
CNN网络中，第一层使用简单的卷积核通常识别的是：竖线、横线、斜线。第二层就可以在第一层的基础上生成长方形，正方形，园等

全连接神经网络，数字识别中，16x16的图片，有28326个参数，数据量太大

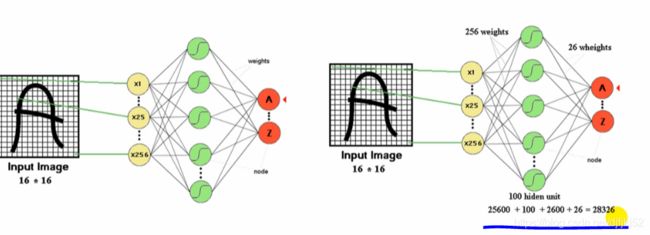
卷积层

• http://m.elecfans.com/article/916036.html
• 明天继续