写这个东西只是记录一下我学过圆方树 \(\text{/cy}\)。
建树
圆方树是一种将图变成树的方法。
首先,把原图中的所有点都看成圆点,我们需要求出图中所有的点双连通分量,可以使用 Tarjan 算法。
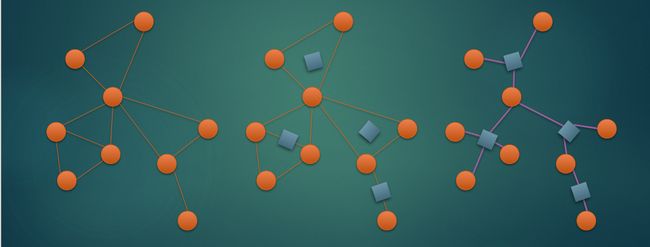
然后,在每一个点双连通分量中间建立一个方点,将此点双连通分量中的所有点向这个方点连边。
这样就可以把图转成树,利用一些树上的性质解题了。
放一张来自 WC PPT 的图。
代码:
int dfn[N], low[N], tim, stk[N], tp, cnt;
int tot, head[N], headc[N], ver[M], nxt[M];
//headc: 原图 head: 圆方树
inline void add(int h[], int u, int v)
{
ver[++tot] = v, nxt[tot] = h[u], h[u] = tot;
}
void Tarjan(int u)
{
dfn[u] = low[u] = ++tim, stk[++tp] = u;
for (int i = headc[u]; i; i = nxt[i])
{
int v = ver[i];
if (!dfn[v])
{
Tarjan(v);
low[u] = min(low[u], low[v]);
if (low[v] == dfn[u])
{
++cnt;
int y = -1;
do
{
y = stk[tp--];
add(head, y, cnt), add(head, cnt, y);
} while (y != v);
add(head, cnt, u), add(head, u, cnt);
}
}
else low[u] = min(low[u], dfn[v]);
}
}
//主函数
int main()
{
n = gi (), m = gi ();
for (int i = 1; i <= m; i+=1)
{
int u = gi (), v = gi ();
add(headc, u, v), add(headc, v, u);
}
cnt = n;
for (int i = 1; i <= n; i+=1)
if (!dfn[i]) Tarjan(i), --tp;
}
性质
- 圆方数上原点和方点交替出现。
- 圆方数的点数小于 \(2n\),因此做题时注意开两倍空间。
- 圆方树上所有不是叶子节点的圆点都是原图中的一个割点。
应用
道路相遇
题面
题意:
\(q\) 次询问,每次询问点 \(u\) 到点 \(v\) 所有简单路径的交。
建出圆方树,问题就转换成圆方树上点 \(u\) 与点 \(v\) 之间圆点的个数。
记录一下树上前缀和,树上差分即可。
代码:
#include
#define DEBUG fprintf(stderr, "Passing [%s] line %d\n", __FUNCTION__, __LINE__)
#define File(x) freopen(x".in","r",stdin); freopen(x".out","w",stdout)
using namespace std;
typedef long long LL;
typedef pair PII;
typedef pair PIII;
template
inline T gi()
{
T f = 1, x = 0; char c = getchar();
while (c < '0' || c > '9') {if (c == '-') f = -1; c = getchar();}
while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return f * x;
}
const int INF = 0x3f3f3f3f, N = 1000003, M = N << 2;
int n, m, q;
int tot, head[N], headc[N], ver[M], nxt[M];
int dfn[N], low[N], tim, stk[N], tp, cnt;
int sum[N];
inline void add(int h[], int u, int v)
{
ver[++tot] = v, nxt[tot] = h[u], h[u] = tot;
}
void Tarjan(int u)
{
dfn[u] = low[u] = ++tim, stk[++tp] = u;
for (int i = headc[u]; i; i = nxt[i])
{
int v = ver[i];
if (!dfn[v])
{
Tarjan(v);
low[u] = min(low[u], low[v]);
if (low[v] == dfn[u])
{
++cnt;
int y = -1;
do
{
y = stk[tp--];
add(head, y, cnt), add(head, cnt, y);
} while (y != v);
add(head, cnt, u), add(head, u, cnt);
}
}
else low[u] = min(low[u], dfn[v]);
}
}
void dfs(int u, int f)
{
sum[u] = (u <= n) + sum[f];
for (int i = head[u]; i; i = nxt[i])
{
int v = ver[i];
if (v == f) continue;
dfs(v, u);
}
}
int dep[N], fa[N], sz[N], son[N], topp[N];
void dfs1(int u, int f)
{
dep[u] = dep[f] + 1, fa[u] = f, sz[u] = 1;
for (int i = head[u]; i; i = nxt[i])
{
int v = ver[i];
if (v == f) continue;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v] > sz[son[u]]) son[u] = v;
}
}
void dfs2(int u, int f)
{
topp[u] = f;
if (!son[u]) return;
dfs2(son[u], f);
for (int i = head[u]; i; i = nxt[i])
{
int v = ver[i];
if (v == fa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
inline int LCA(int u, int v)
{
while (topp[u] != topp[v])
{
if (dep[topp[u]] < dep[topp[v]]) swap(u, v);
u = fa[topp[u]];
}
if (dep[u] < dep[v]) return u;
return v;
}
int main()
{
//File("");
n = gi (), m = gi ();
for (int i = 1; i <= m; i+=1)
{
int u = gi (), v = gi ();
add(headc, u, v), add(headc, v, u);
}
cnt = n;
Tarjan(1);
dfs(1, 0);
q = gi ();
dfs1(1, 0); dfs2(1, 1);
while (q--)
{
int u = gi (), v = gi ();
int lca = LCA(u, v);
printf("%d\n", sum[u] + sum[v] - sum[lca] - sum[fa[lca]]);
}
return 0;
}
APIO2018 铁人两项
题面
题意:
问有多少组 \(s\),\(c\) 和 \(f\),满足存在从 \(s\) 到 \(c\) 和从 \(c\) 到 \(f\) 的简单路径。
首先介绍一个点双的性质:对于一个点双中的两个点 \(u\) 和 \(v\),它们之间简单路径的并集恰好等于这个点双。
然后问题就转换成了:固定 \(s\) 和 \(f\),问有多少个合法的 \(c\)。
考虑圆方树上两圆点在原图中所有简单路径的并,将这个问题转换到圆方树上就变成 两圆点之间的路径 与 路径上方点所在点双中的所有点。
这个问题很好求解,我们把圆方树上每个方点的权值设为这个点双中的点数,圆点的权值设为 \(-1\),答案即为圆方树上 \(\sum\) 两点之间所有点的权值之和。
代码:
#include
#define DEBUG fprintf(stderr, "Passing [%s] line %d\n", __FUNCTION__, __LINE__)
#define File(x) freopen(x".in","r",stdin); freopen(x".out","w",stdout)
using namespace std;
typedef long long LL;
typedef pair PII;
typedef pair PIII;
typedef pair PLI;
template
inline T gi()
{
T f = 1, x = 0; char c = getchar();
while (c < '0' || c > '9') {if (c == '-') f = -1; c = getchar();}
while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return f * x;
}
const int INF = 0x3f3f3f3f, N = 200003, M = N << 3;
int n, m;
int tot, head[N], headc[N], ver[M], nxt[M];
int dfn[N], low[N], tim, stk[N], tp;
int val[N], sz[N];
int cnt;
LL ans;
int num;
inline void add(int h[], int u, int v)
{
ver[++tot] = v, nxt[tot] = h[u], h[u] = tot;
}
void Tarjan(int u)
{
++num;
dfn[u] = low[u] = ++tim, stk[++tp] = u;
for (int i = head[u]; i; i = nxt[i])
{
int v = ver[i];
if (!dfn[v])
{
Tarjan(v);
low[u] = min(low[u], low[v]);
if (low[v] == dfn[u])
{
val[++cnt] = 0;
int y = -1;
do
{
y = stk[tp--];
add(headc, y, cnt), add(headc, cnt, y);
++val[cnt];
} while (y != v);
add(headc, u, cnt), add(headc, cnt, u);
++val[cnt];
}
}
else low[u] = min(low[u], dfn[v]);
}
}
void dfs(int u, int f, int mn)
{
sz[u] = (u <= n);
for (int i = headc[u]; i; i = nxt[i])
{
int v = ver[i];
if (v == f) continue;
dfs(v, u, mn);
ans += (LL)2 * val[u] * sz[u] * sz[v];
sz[u] += sz[v];
}
ans += (LL)2 * val[u] * sz[u] * (mn - sz[u]);
}
int main()
{
//File("");
n = gi (), m = gi ();
for (int i = 1; i <= m; i+=1)
{
int u = gi (), v = gi ();
add(head, u, v), add(head, v, u);
}
for (int i = 1; i <= n * 2; i+=1) val[i] = -1;
cnt = n;
for (int i = 1; i <= n; i+=1)
if (!dfn[i])
{
num = 0;
Tarjan(i);
--tp;
dfs(i, 0, num);
}
printf("%lld\n", ans);
return 0;
}
参考学习
- https://www.cnblogs.com/PinkRabbit/p/10446473.html
- https://www.cnblogs.com/cjyyb/p/9098400.html