最大公约数几种算法分析
程序设计方法学上机——(一)
- 题目:
运行最大公约数的常用算法,进行程序的调试与测试,要求程序设计风良好,并添加异常处理模块(如非法输入)。
- 辗转相除法:
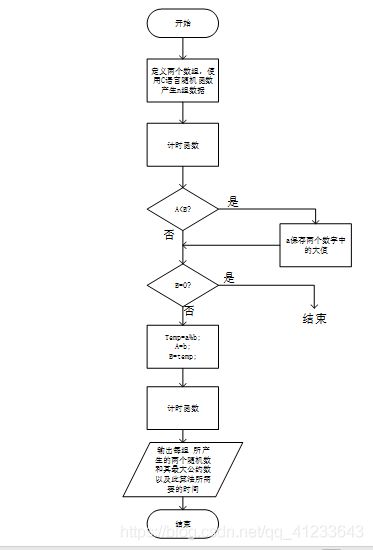
其算法过程为: 前提:设两数为a,b设其中a 做被除数,b做除数,temp为余数
==>大数放a中、小数放b中;
==>求a/b的余数;
==>若temp=0则b为最大公约数;
==>如果temp!=0则把b的值给a、temp的值给a;
==>返回第二步;
(1)非递归
(2)递归
- 穷举法:
穷举法(也叫枚举法)穷举法求两个正整数的最大公约数的解题步骤:从两个数中较小数开始由大到小列举,直到找到公约数立即中断列举,得到的公约数便是最大公约数 。
- 更相减损法:
==>任意给定两个正整数;判断它们是否都是偶数。若是,则用2约简;若不是则执行第二步。
==>以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止。
则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。
其中所说的“等数”,就是最大公约数。求“等数”的办法是“更相减损”法。所以更相减损法也叫等值算法。
- Stein算法
对两个正整数 x>y :
1.均为偶数 gcd( x,y ) =2gcd( x/2,y/2 );
2.均为奇数 gcd( x,y ) = gcd( (x+y)/2,(x-y)/2 );
2.x奇y偶 gcd( x,y ) = gcd( x,y/2 );
3.x偶y奇 gcd( x,y ) = gcd( x/2,y ) 或 gcd( x,y )=gcd( y,x/2 );
现在已经有了递归式,还需要再找出一个退化情况。注意到 gcd( x,x ) = x ,就用这个。
- 非递归
- 递归
- 算法构造:
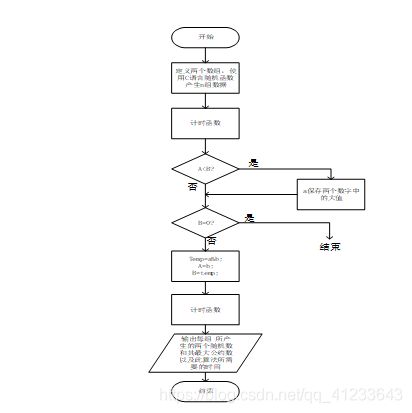
- 辗转相除流程图:
(1)非递归:
(2)递归:
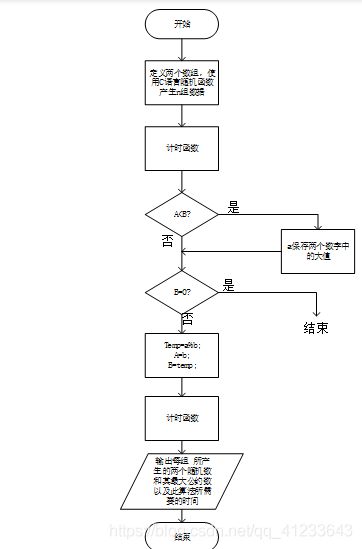
- 穷举法流程图:
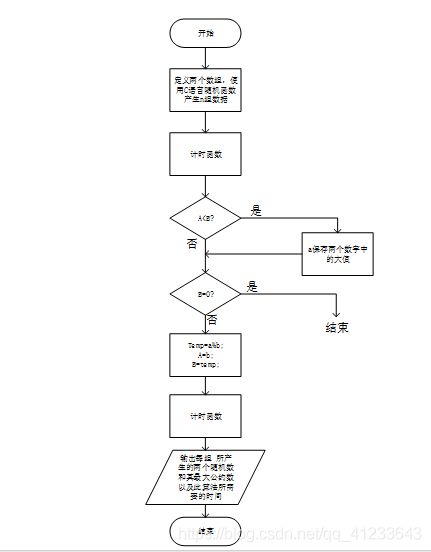
- 更相减损法流程图:
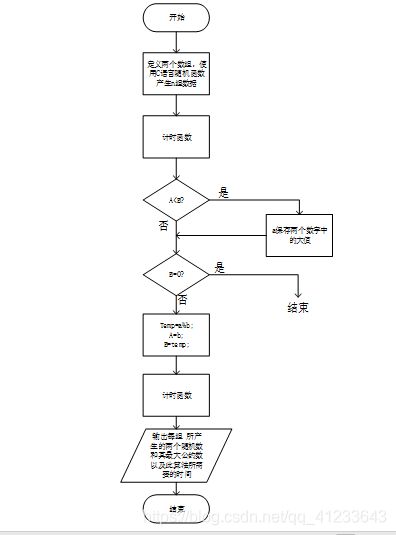
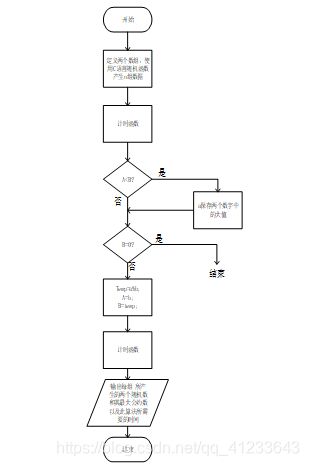
- Stein算法流程图:
- 非递归:
- 递归:
- 算法实现:(源码)
- 辗转相除法:
(1)非递归:
//辗转相除法
/*函数嵌套调用*/
#include /*输入输出类头文件*/
#include
#include
#include
int GCD (int a,int b) /*自定义函数求两数的最大公约数*/
{
int temp; /*定义整型变量,用于交换变量时做临时变量*/
if(a - 递归:
//辗转相除法
/*函数递归*/
#include /*输入输出类头文件*/
#include
#include
int GCD (int a,int b) /*自定义函数求两数的最大公约数*/
{ if(a%b==0) /*看b是否是最大公约*/
return b;
else
return GCD(b,a%b);
}
int main() /*主函数*/
{
/*计时函数所需定义语句*/
double dur;
LARGE_INTEGER time_start;
LARGE_INTEGER time_over;
double dqFreq;
LARGE_INTEGER f;
QueryPerformanceFrequency(&f);
dqFreq=(double)f.QuadPart;
int gcd; /*变量用于存最大公约数*/
int i,a[100001],b[100001]; /*定义两个数组*/
srand(10); /*随机函数*/
for(i=0;i<100000;i++)
{
a[i]=1+rand()%100;
b[i]=1+rand()%100;
}
QueryPerformanceCounter(&time_start);
for(i=0;i<100000;i++)
{
gcd=GCD(a[i],b[i]); /*自定义主调函数*/
printf("随机数为%d,%d",a[i],b[i]);
printf("这两个整数的最大公约数是 %d\n\n",gcd); /*输出最大公约数*/
QueryPerformanceCounter(&time_over);
dur=(time_over.QuadPart-time_start.QuadPart)/dqFreq;
}
printf("所需时间%f seconds\n",dur);
return 0;
}
- 穷举法:
//穷举法
#include /*输入输出类头文件*/
#include
#include
#include
#include
int GCD (int a,int b) /*自定义函数求两数的最大公约数*/
{
int temp; /*定义义整型变量*/
temp=(a>b)?b:a; /*采种条件运算表达式求出两个数中的最小值*/
while(temp>0)
{
if (a%temp==0&&b%temp==0) /*只要找到一个数能同时被a,b所整除,则中止循环*/
break;
temp--; /*如不满足if条件则变量自减,直到能被a,b所整除*/
}
return (temp); /*返回满足条件的数到主调函数处*/
}
int main()
{
/*计时函数所需定义语句*/
double dur;
LARGE_INTEGER time_start;
LARGE_INTEGER time_over;
double dqFreq;
LARGE_INTEGER f;
QueryPerformanceFrequency(&f);
dqFreq=(double)f.QuadPart;
int gcd; /*变量用于存最大公约数*/
int i,a[100001],b[100001]; /*定义两个数组*/
srand(10); /*随机函数*/
for(i=0;i<100000;i++) /*通过循环输入规模*/
{
a[i]=1+rand()%100;
b[i]=1+rand()%100;
}
QueryPerformanceCounter(&time_start);
for(i=0;i<100000;i++)
{
gcd=GCD(a[i],b[i]); /*自定义主调函数*/
printf("随机数为%d,%d",a[i],b[i]);
printf("这两个整数的最大公约数是 %d\n\n",gcd); /*输出最大公约数*/
QueryPerformanceCounter(&time_over);
dur=(time_over.QuadPart-time_start.QuadPart)/dqFreq;
}
printf("所需时间%f seconds\n",dur);
return 0;
}
- 更相减损:
//更相减损
#include /*输入输出类头文件*/
#include
#include
#include
#include
int GCD(int m,int n)
{
int i=0,temp,x;
while(m%2==0 && n%2==0) //判断m和n能被多少个2整除
{
m/=2;
n/=2;
i+=1;
}
if(mx)?n:x;
n=(n
- Stein算法:
- 非递归:
//stein
/*非递归*/
#include /*输入输出类头文件*/
#include
#include
#include
#include
int SteinGCD( unsigned int x, unsigned int y )
/* return the greatest common divisor of x and y */
{
int factor = 0;
int temp;
if ( x < y )
{
temp = x;
x = y;
y = temp;
}
if ( 0 == y )
{
return 0;
}
while ( x != y )
{
if ( x & 0x1 )
{/* when x is odd */
if ( y & 0x1 )
{/* when x and y are both odd */
y = ( x - y ) >> 1;
x -= y;
}
else
{/* when x is odd and y is even */
y >>= 1;
}
}
else
{/* when x is even */
if ( y & 0x1 )
{/* when x is even and y is odd */
x >>= 1;
if ( x < y )
{
temp = x;
x = y;
y = temp;
}
}
else
{/* when x and y are both even */
x >>= 1;
y >>= 1;
++factor;
}
}
}
return ( x << factor );
}
int main()
{
//计时函数所需要定义的语句
double dur;
LARGE_INTEGER time_start;
LARGE_INTEGER time_over;
double dqFreq;
LARGE_INTEGER f;
QueryPerformanceFrequency(&f);
dqFreq=(double)f.QuadPart;
int gcd;//定义变量用于存放最大公约数
int i,a[100001],b[100001];//定义两个数组
srand(10); //随机函数
for(i=0;i<100000;i++)//通过循环控制规模
{
a[i]=1+rand()%100;
b[i]=1+rand()%100;
}
QueryPerformanceCounter(&time_start);
for(i=0;i<100000;i++)
{
gcd=SteinGCD(a[i],b[i]);
printf("随机数为%d,%d",a[i],b[i]);
printf("这两个整数的最大公约数是 %d\n\n",gcd); /*输出最大公约数*/
//printf("所需时间%f\n",(double)(end-start)/CLOCKS_PER_SEC);
QueryPerformanceCounter(&time_over);
dur=(time_over.QuadPart-time_start.QuadPart)/dqFreq;
}
printf("所需时间%f seconds\n",dur);
return 0;
}
- 递归:
//stein
/*递归实现*/
#include /*输入输出类头文件*/
#include
#include
#include
#include
int SteinGCD(int u,int v)
{
if (u == 0) return v;
if (v == 0) return u;
// look for factors of 2
if (~u & 1) // u is even
{
if (v & 1) // v is odd
return SteinGCD(u >> 1, v);
else // both u and v are even
return SteinGCD(u >> 1, v >> 1) << 1;
}
if (~v & 1) // u is odd, v is even
return SteinGCD(u, v >> 1);
// reduce larger argument
if (u > v)
return SteinGCD((u - v) >> 1, v);
return SteinGCD((v - u) >> 1, u);
}
int main()
{
//计时函数所需要定义的语句
double dur;
LARGE_INTEGER time_start;
LARGE_INTEGER time_over;
double dqFreq;
LARGE_INTEGER f;
QueryPerformanceFrequency(&f);
dqFreq=(double)f.QuadPart;
int gcd;//定义变量用于存放最大公约数
int i,a[100001],b[100001];//定义两个数组
srand(10); //随机函数
for(i=0;i<100000;i++)//通过循环控制规模
{
a[i]=1+rand()%100;
b[i]=1+rand()%100;
}
QueryPerformanceCounter(&time_start);
for(i=0;i<100000;i++)
{
gcd=SteinGCD(a[i],b[i]);
printf("随机数为%d,%d",a[i],b[i]);
printf("这两个整数的最大公约数是 %d\n\n",gcd); /*输出最大公约数*/
//printf("所需时间%f\n",(double)(end-start)/CLOCKS_PER_SEC);
QueryPerformanceCounter(&time_over);
dur=(time_over.QuadPart-time_start.QuadPart)/dqFreq;
}
printf("所需时间%f seconds\n",dur);
return 0;
}
- 调试、测试:
- 调试:
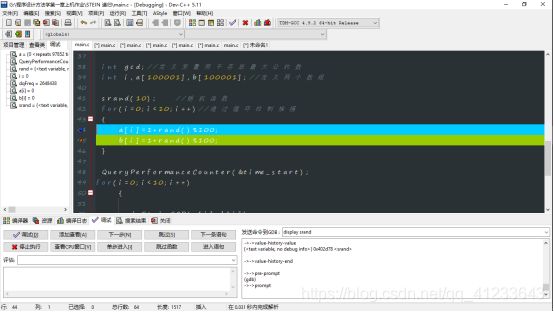
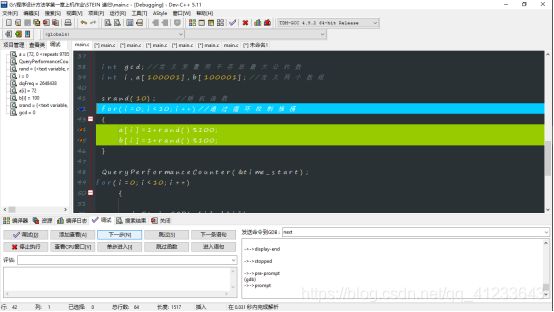
- 随机数调试:(以3组数据为例)
===>观察a[i],b[i]当i在变化是每次的不同随机数,此时为未开始,二者为0;
===>i=0时,a[i]=72,b[i]=100
===>i=1时,a[i]=73,b[i]=95
===>i=2,a[i]=98,b[i]=97
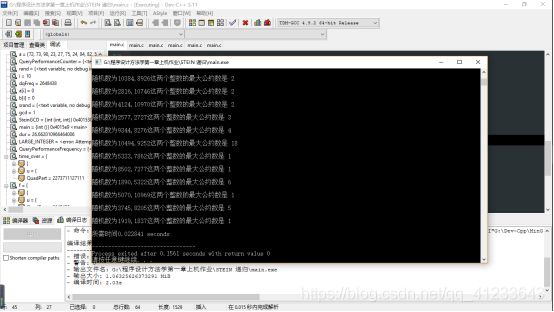
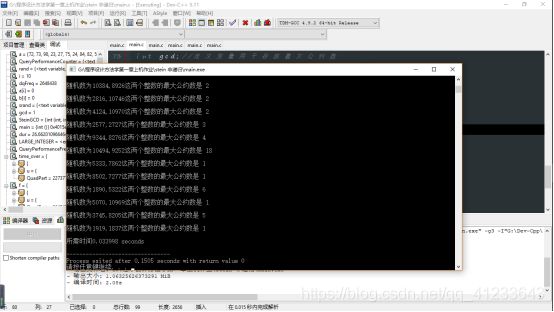
- 测试:
--Stein递归--
--Stein非递归--
--更相减损--
--穷举法--
--辗转相除递归--
--辗转相除非递归--
- 分析:
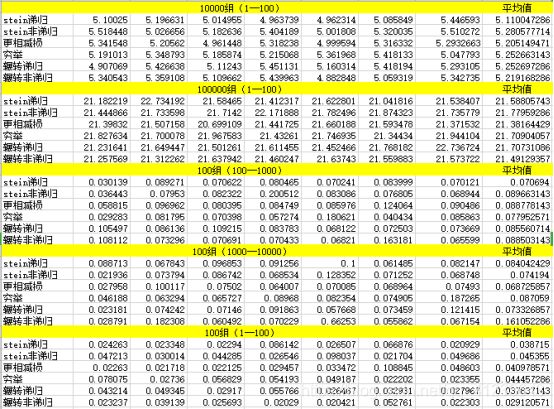
--测试时间的表格结果--
- 6种算法比较:规模相同,数据范围相同:
在100组数据和1000组数据:辗转相除非递归算法效率比较高;
在10000组数据:stein算法效率较高
- 同一种算法比较,数据范围不同时,运行时间的变化幅度:
对于6种方法,当规模相同,随着随机数的范围不同,运行时间都有所增加,其中辗转相除非递归增加最为明显,
- 总结:
本程序运用六种代码来测试效率,采取了平均值来避免偶然性误差。
本实验为了测试求最大公约数的算法效率,在实验过程中,遇到了一些问题。
- 刚开始手动输入两位两位数据,发现效率低且不能进行大规模数据测试
- 计时函数在用的时候是在网上看了一些程序采用到本程序上
不足:
- 测试数据没有实现数据为0时求公约数
- 每次运行时间差异较大,没有找到原因所在
- 感觉数据测试不是很准确,数据规模范围没有达到比较好的地步
如果有什么错误请各位大神指出来,完成之后记得撒花撒花~~