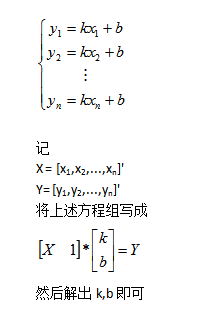MATLAB中的曲线拟合

1.最小二乘法

MATLAB提供了polyfit函数命令进行最小二乘的曲线拟合。

polyfit命令的调用格式如下：

调用格式                                                    说明

p = polyfit(x,y,n)                                  对x和y进行n维多项式的最小二乘拟合，输出结果p为含有n+1个元素的行向量，该向量以维数

                                                             递减的形式给出拟合多项式的系数

[p,s] = polyfit(x,y,n)                             结果中的s包括R、df和normr，分别表示对x进行QR分解的三角元素、自由度、残差

[p,s,mu] = polyfit(x,y,n)                      在拟合过和中，首先对x进行数据标准化处理，以在拟合中消除量纲等的影响，mu包含两个元素，

                                                              分别是标注化处理过程中使用的x的均值和标准差

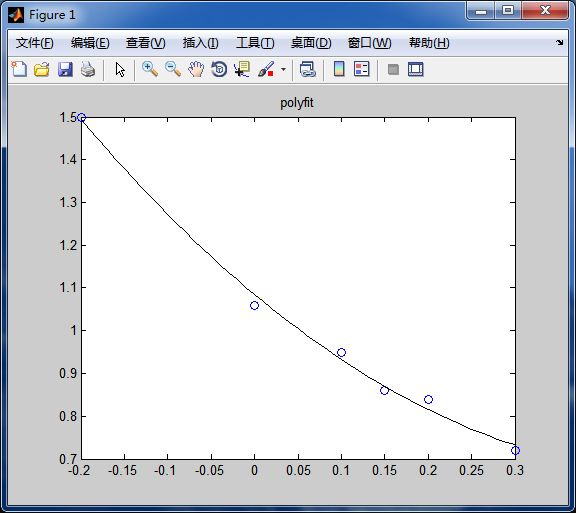
例： 用二次多项式拟合下列数据

x                          0.1                     0.2                      0.15                     0.0                       -0.2                     0.3

y                        0.95                    0.84                    0.86                     1.06                     1.50                    0.72

>> x = [0.1, 0.2, 0.15, 0, -0.2, 0.3];
>> y = [0.95, 0.84, 0.86, 1.06, 1.50, 0.72];
>> p = polyfit(x,y,2)

p =

    1.7432   -1.6959    1.0850

>> xi = -0.2 : 0.01: 0.3;
>> yi = polyval(p,xi);
>> plot(x,y,'o',xi,yi,'k');
>> title('polyfit');
>> 

 例：用二次多项式拟合下列数据：

x                         0.5                         1                       1.5                           2                             2.5                          3

y                          1.75                    2.45                   3.81                       4.8                           8                            8.6

>> clear
>> x = 0.5:0.5:3;
>> y = [1.75,2.45,3.81,4.8,8,8.6];
>> [p,s] = polyfit(x,y,2)

p =

    0.4900    1.2501    0.8560


s = 

        R: [3x3 double]
       df: 3
    normr: 1.1822

>> 

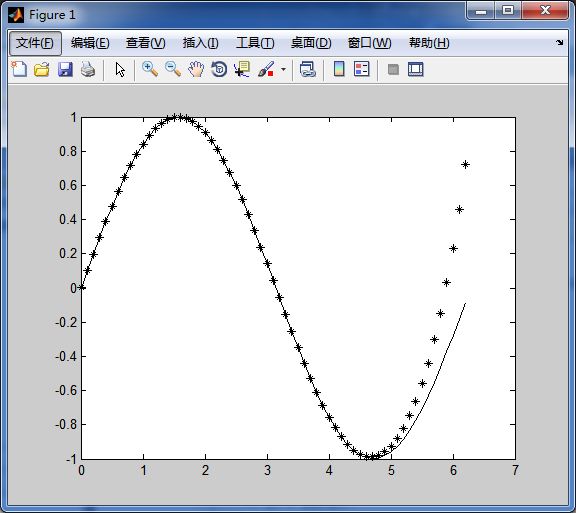
例：在[0,π]区间上对正弦函数进行拟合，然后在[0,2π]区间上画出图形，比较拟合区间和非拟合区间的图形，考察拟合的有效性。

>> clear
>> x = 0:0.1:pi;
>> y = sin(x);
>> [p, mu] = polyfit(x,y,9);
>> x1 = 0:0.1:2*pi;
>> y1 = sin(x1);
>> y2 = polyval(p,x1);
>> plot(x1,y2,'k*',x1,y1,'k-')
>> 

2.直线的最小二乘拟合

一组数据[x1,x2,...,xn]和[y1,y2,...yn]，已知x和y成线性关系，即 y = kx + b，对该直线进行拟合，就是求出选定系数k和b的过程。如果将直线拟合看作是一阶多项式拟合，那么可以直接利用最小二乘法来进行计算。由于最小二乘法直线拟合在数据处理中有其特殊的重要作用，这里再单独介绍另一种方法：利用矩阵除法进行最小二乘拟合。

先说下原理：

编写一个M文件如下：

function[k,b] = linefit(x,y)
n = length(x);
x = reshape(x,n,1);          %生成列向量
y = reshape(y,n,1);          
A = [x,ones(n,1)];           %连接矩接A
bb = y;
B = A'*A;
bb = A'*bb;
yy = B\bb;
k = yy(1);                   %得到k
b = yy(2);                   %得到b

例：将以下数据进行直线拟合

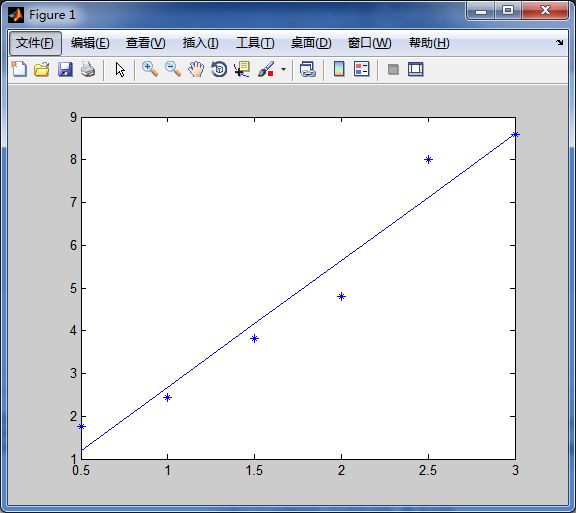
x                      0.5                        1                         1.5                        2                          2.5                            3

y                      1.75                     2.45                    3.81                    4.8                         8                              8.6

>> x = [0.5 1 1.5 2 2.5 3];
>> y = [1.75 2.45 3.81 4.8 8 8.6];
>> [k,b] = linefit(x,y)

k =

    2.9651


b =

   -0.2873

>> y1 = polyval([k,b],x);
>> plot(x,y1);
>> hold on
>> plot(x,y,'*')
>>