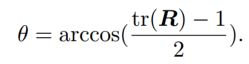视觉slam爬坑——高翔深蓝学院——第二讲——三维空间刚体运动

1月6日补充
Eigen补充参考学习的资料
Eigen官网：http://eigen.tuxfamily.org/dox/group__QuickRefPage.html#QuickRef_Types
Eigen解方程组：https://blog.csdn.net/u013354805/article/details/48250547
Eigen快速入门：https://www.cnblogs.com/python27/p/EigenQuickRef.html
Eigen讲解资料：https://blog.csdn.net/houjixin/article/details/8494582

补充的C++内容
C++这个东西博大精深，slam方面要用到的除了C++的基本操作外，要学习包括类和对象、继承、重载。可以通过这个网站了解入门操作
http://www.runoob.com/cplusplus/cpp-constructor-destructor.html
模板和模板类：http://www.cnblogs.com/gaojun/archive/2010/09/10/1823354.html
关键在于写代码和看代码，不是一两天可以学会搞定。

（1）本节课内容

1、旋转矩阵 2、旋转向量与欧拉角 3、四元数 4、Eigen库用法

（2）需要的基础知识

1、线性代数：高斯消元法解线性方程组，行列式基本运算，矩阵四则运算与基础知识，逆矩阵，伴随矩阵，矩阵初等变换，向量基本运算（注意矩阵和向量之间内积外积区别）基本上大学线性代数前4，5章节的内容都需要过一遍，看的快点，用时2小时内
2、C++：因人而异了，C++Primer第一部分基础章节过一遍，然后重点看下类、引用，继承，重载、模板类的部分。
3、有点空间想象力。

（3）开发环境

编译平台：ubuntu16.04，
编译软件：IDE：Clion 编译器：Cmake 语言标准：C++11
关于Clion安装请移步：https://blog.csdn.net/weixin_38593194/article/details/85122716
关于Cmake用法请移步：https://blog.csdn.net/weixin_38593194/article/details/85077946

（4）达成标准

线性代数：

1、说明Ax=b在什么情况下有解？有唯一解？无解？
2、高斯消元法原理，行列式计算
3、矩阵内外积运算区别，矩阵初等变换与四则运算
4、如何利用矩阵解线性齐次方程组
5、QR分解原理
6、Cholesky分解原理

旋转的表达：

1、理解坐标系间的欧氏变换，旋转矩阵的构成，旋转轴和旋转角与罗德里格斯公式。
2、理解欧拉角
3、四元数的四则运算
4、用四元数表示旋转矩阵

Eigen使用

1、使用Eigen进行矩阵的四则运算
2、编程实现 A 为 100 × 100 随机矩阵时，⽤ QR 和 Cholesky 分解求 x 的程序。

（5）填坑

三维旋转：旋转矩阵，欧拉角，四元数：http://www.cnblogs.com/yiyezhai/p/3176725.html
有兴趣可以看看

0、旋转矩阵

这块是学了李群和李代数后觉得需要补充出来的内容和性质，跟李群和李代数关系不大，跟本章后面需要理解和明确的定义和性质有关
首先先来定义旋转的作用对象——刚体
1、刚体：在外力作用下处于平衡状态的物体，如果物体的变形不影响其平衡位置及作用力的大小和方向，则该物体可视为刚体。（这个定义表示作用力带来的速度的方向和旋转等变换也是不受形变影响的）。
2、点：在几何学上点是 没有大小而只有位置，即点存在于三维空间中的某一个位置。
3、向量： 可以形象化地表示为 带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。 （请勿将向量与它的坐标两个概念混淆，向量有方向是矢量，坐标无方向是标量，坐标表示的是向量在某个坐标系下的位置）
例如，在线性空间的基（e1,e2,e3），向量a（a1,a2,a3）在该基向量下的坐标是

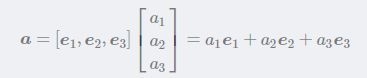
左手坐标系和右手坐标系，常用右手

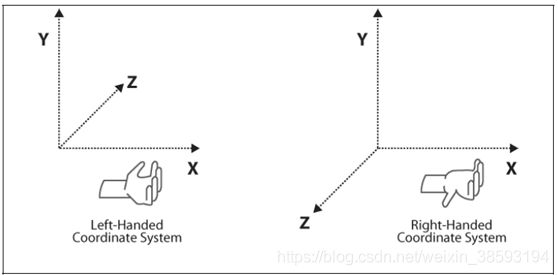
4、向量运算
对于三维向量a(a1,a2,a3),b(b1,b2,b3)
向量内积

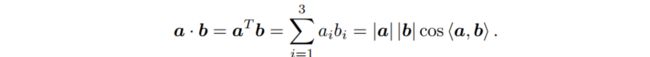
向量外积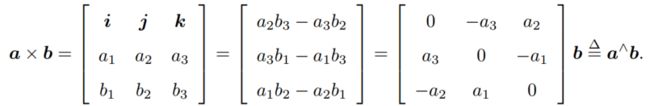
三维空间里，外积的方向垂直于a,b，是a，b共同的法向量，大小为两个向量张成的四边形面积。
即：a×b=|a||b|sin
符号^表示反对称矩阵。扩充反对称矩阵的县官定义和性质

性质1
两个反对称矩阵A,B，A±B也为反对称矩阵
性质2
对于反对称矩阵A，A的转置，xA都为反对称矩阵（x为常数）

上面向量外积的公式需要记住，后面会用到。

1、坐标系之间的欧式变换

两个坐标系之间的旋转关系和平移关系，统称坐标系之间的变换。
将地面设置为惯性坐标系或者世界坐标系W（认定其为固定不动的），机器人为移动坐标系C（随着运动可变坐标系）。如图Xw、Yw、Zw定义世界坐标系。机器人运动过程中，假设移动坐标系定义为Xc，Yc，Zc。某定点p，在移动机器人上的相机视野中Pc，在世界坐标系下看Pw，对同一个点有两个坐标，他们之间有什么关系？
这时可以用一个矩阵T表述其中的转换关系，T表述旋转和平移两种操作。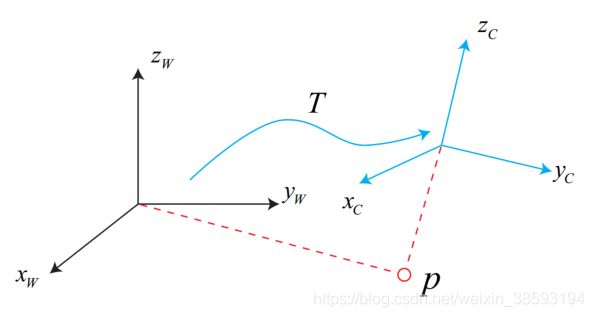
先理解旋转
我们设某个单位正交基(e1; e2; e3) 经过一次旋转，变成了 (e′ 1; e′ 2; e′ 3)。那么，对于同一个向量 a（注意该向量并没有随着坐标系的旋转而发生运动），它在两个坐标系下的坐标为 [a1; a2; a3]T 和 [a′ 1; a′ 2; a′ 3]T。根据坐标的定义，有：


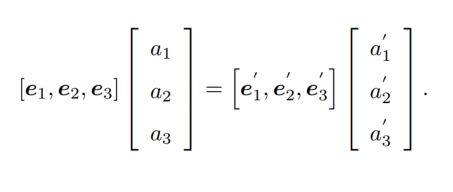
用旋转矩阵R可以用来描述相机的旋转。
旋转矩阵特殊的性质：
它是一个行列式为 1 的正交矩阵‹。反之，行列式为 1 的正交矩阵也是一个旋转矩阵。旋转角度越小，R越接近单位矩阵。旋转矩阵的集合定义如下：

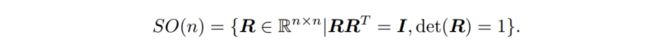
SO(n) 是特殊正交群（Special Orthogonal Group）的意思。解释“群”的内容留到下一讲
再看平移
搞定了旋转，任何变换的平移都可看作在世界坐标系W下的三维移动，所以平移是不需要进行任何矩阵变换 的，设世界坐标系中向量a，经过一次旋转R和一次平移t后得到a‘，则把平移和旋转合在一起，有：a’=Ra+t
这就是本节一开始所说的T（变换）。
——————————————————————1月7日补充内容————————————————————————

1.9变换矩阵

这里引出的是变换矩阵的定义，后面李代数会用到，本节中需要知道变换矩阵怎么来的，表现成什么样子就行。
上面我们使用a’=Ra+t表现了一次旋转后的关系，如果再进行2次连续的变换呢？a"=R1a’+t1。那n次该如何表示呢？


由此，旋转可用旋转矩阵R组成的特殊正交群SO(3)表示，将平移和旋转放在一起可用变换矩阵T组成的特殊欧式群SE(3)表述。

2、旋转向量

任意旋转都可以用一个旋转轴和一个旋转角来表示，于是有了旋转向量。使用一个向量，其方向与旋转轴一致，长度等于旋转角。旋转向量就是下节要讲的SO(3)的李代数so(3)，而变换矩阵的李代数则是se(3)旋转向量是三维的，变换矩阵的是6维（三维旋转+三维平移）
接下来具体推一下旋转向量和旋转矩阵之间如何转换的。从向量到旋转矩阵的过程由罗德里格斯公式。
假设旋转轴n，角度θ的旋转，则旋转向量为θn****这个公式很重要，需要看结论的移步本节最后分割线。
由图1得推导过程：

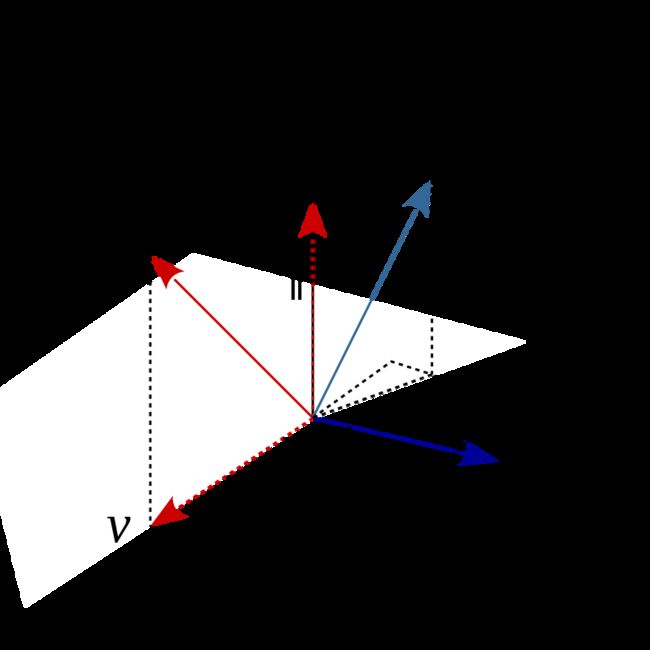
图1
设k是定义旋转轴的单位矢量，并且令v是任何矢量以k为角度θ旋转（右手规则，图中为逆时针）。
使用点和叉积，矢量v可以分解为平行和垂直于轴k的分量，

其中与k平行的分量是

ps：k是单位矢量，(v·k)k=|v||k|cosk=|v|k(k表示矢量方向)
称为矢量投影的v上ķ

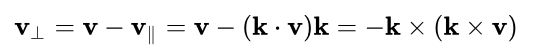
矢量ķ × v可以被看作是副本v ⊥由90°逆时针旋转ķ，所以它们的大小相等，但方向是垂直的。同样地，矢量ķ ×（ķ × v）的副本v ⊥通过逆时针旋转180°约ķ，使得ķ ×（ķ × v）和v ⊥是在幅度，但方向相反相等（即它们各自的底片其他，因此减号）。（推导过程是旋转向量的概念，用旋转轴和旋转角表示旋转向量）
则平行于轴的分量在旋转下不会改变幅度或方向，

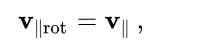
垂直分量会改变方向但保持其大小

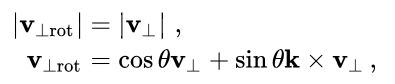
（上面公式描述的是一个旋转的过程，见下图）
ps：向量的加法表述向量=水平分量+垂直分量

这种旋转是正确的，因为矢量v ⊥和ķ × v具有相同的长度，并ķ × v是v ⊥通过逆时针旋转90°左右ķ。使用三角函数正弦和余弦对v⊥和k × v进行适当的缩放，得到旋转的垂直分量。旋转分量的形式类似于2D平面极坐标（r，θ）中的径向矢量 在笛卡尔的基础上
其中e x，e y是指示方向的单位矢量。

现在完全旋转的矢量是

通过替换的定义v ∥rot和v ⊥rot在方程结果


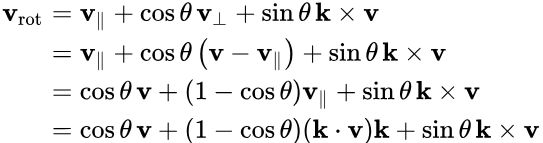
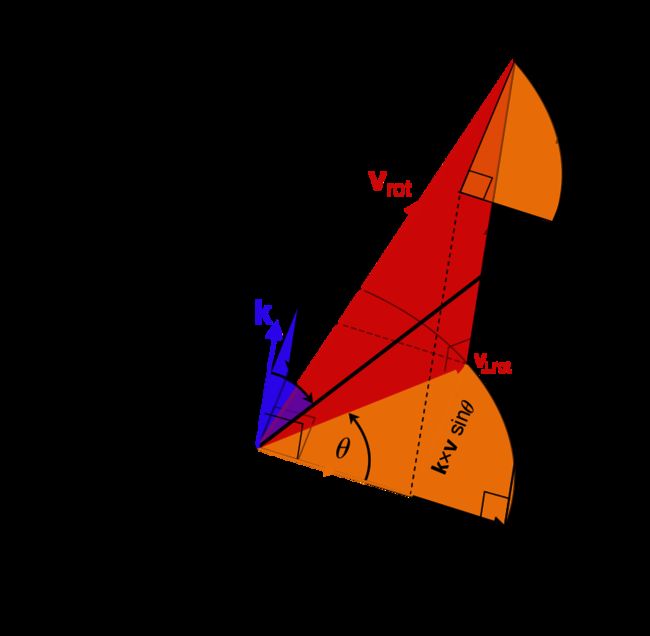
推导的罗德里格斯轮换公式

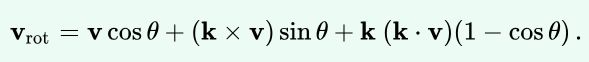
对于旋转矩阵R和旋转向量的关系可以表述为

反之可计算从一个旋转矩阵到旋转向量的转换，对于转角θ

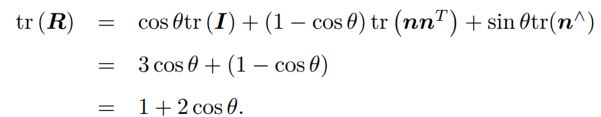
===================================================================分割线顶顶顶顶

3、欧拉角

在航空或者航模里经常用到，是一种符合人的思维、十分直观的描述物体在三个轴线上旋转的方式。
对欧拉角的理解参考：https://blog.csdn.net/sinat_27456831/article/details/50042915
但是欧拉角由万向节死锁的问题，在计算的过程中有奇异性，所以计算的时候不采用，在人机交互的时候采用欧拉角，会比较直观。

4、四元数

四元数是一种紧凑的无奇异的表述三维向量的方式。

i，j，k为三个虚部，他们满足关系式

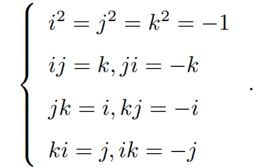
由于其特殊性，有时候也采用一个标量一个向量的形式来表达四元数

5、Eigen

Eigen是一个矩阵运算库，这部分其实不难，有个学习的例程，照着敲敲就会了，分享一个例子。
链接：https://pan.baidu.com/s/1Lb7H7YiceNo6lW_UF71ptg
提取码：k9p2

6、C++11

主要难点在于C++11，，，，引用，继承，模板类。等我学习两天再来补充。