【线代】行/列分块矩阵中向量正交有什么用？如何表述？向量正交和线性无关有什么关系？

目录

一、向量正交

二、向量线性无关

三、二者关系

1. 两个向量

2. 正交向量组

3. 一个向量与一个向量组正交

四、小结

---

一、向量正交

1. 定义

两向量正交，那么内积 (α，β)=0，或者写作点乘 α • β=0。

2. 表述

向量是一种有序数组，如a=(a1，a2，a3，……)，本身是表示方向的。内积或者说点乘，就是两向量坐标对应位置的乘积的和。

《向量正交是什么意思》：https://zhidao.baidu.com/question/1608819442654220827.html?qbl=relate_question_0

《向量内积（点乘）和外积（叉乘）概念及几何意义》：https://www.cnblogs.com/gxcdream/p/7597865.html

---

但是，在矩阵需要分块时，常引入向量，分为列向量或行向量。

行向量乘列向量才是内积，列向量乘行向量是矩阵。行向量不可乘行向量，列向量也不可乘列向量。

因此在表述时，有如下几种情况。由于矩阵常常按照列分块或按行分块，一般出现同类型向量较多，也即后两种。

• 行向量α与列向量β正交，则。
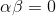• 行向量α与行向量β正交，则。
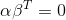• 列向量α与列向量β正交，则。

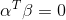二、向量线性无关

两个向量线性无关，即一个不可被另一个线性表示，即不平行。

一个向量与一个向量组线性无关，即不可被其线性表示，不

三、二者关系

1. 两个向量

证明过程：《线性代数：正交的向量一定线性无关吗？》：https://zhidao.baidu.com/question/1818343757400219548.html

结论：两个向量正交，那么一定线性无关。两个向量线性无关，不一定就是正交。

理解记忆：正交是指，两个向量的夹角为90°。（无所谓行向量、列向量，这里是一种n维空间的坐标关系）

线性无关是指，两个向量不平行（或者重合），就是夹角不为0°或180°。

2. 正交向量组

两两正交的非零向量组是正交向量组，其组内向量一定线性无关。反之未必，即线性无关未必正交。

《向量组的正交性》：https://wenku.baidu.com/view/859595d084254b35eefd3498.html

证明如这篇文章。最后的例题也可看出，一个向量与一个向量组正交，实际是它与组内向量分别两两正交。正交的定义是发生在两个向量间的。

3. 一个向量与一个向量组正交

一个向量与一个向量组正交，是它与组内向量分别两两正交。

---

《向量组和向量正交是什么意思？》：https://zhidao.baidu.com/question/1389218406721751020.html

显然是提问者（1）中的意思。不要看解答，答非所问。

《向量组a1....an和一个向量β正交，是什么意思？》：https://zhidao.baidu.com/question/332952536677157125.html?qbl=relate_question_0

这个解答清楚。

《证明：如果向量b与向量组a1,a2,...,as中的每个向量都正交，则b与a1，a2，...，as的任意线性组合k1a1+k2a2+...+ksas也正交》：https://zhidao.baidu.com/question/1179635885024901859.html?qbl=relate_question_5

一个相关的小证明题，帮助理解。

四、小结

1. 向量正交即垂直，发生在两个向量间。正交向量的坐标内积为0，注意区分表述形式。

• 行向量α与行向量β正交，则。
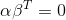• 列向量α与列向量β正交，则。

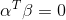2. 向量线性无关，即不可被线性表示，两向量不共线，也有向量与一个向量组线性无关（即不在向量组表示的空间内）。

3. 两个向量正交，那么一定线性无关。两个向量线性无关，不一定就是正交。

4. 两两正交的非零向量组是正交向量组，其组内向量一定线性无关。反之未必，即线性无关未必正交。

5. 一个向量与一个向量组正交，是它与组内向量分别两两正交。

强烈推荐一本书！《线性代数的几何意义》任广千（豆瓣主页）。

从几何意义去理解线性代数非常重要，可以把各种概念串联起来。

还在读，等读完应该要写一些读书笔记。