Javascript二维质点运动模拟
原创不易,未经允许不得转载
阅读提示
- 以下内容涉及到线性代数,如果你已经忘记线代或者没有学过,可以先看看平面向量。
- 绘制使用的JS canvas 2d,以及配合requestAnimationFrame进行循环,不熟悉的朋友可以看我之前的文章。不过本文主要讲碰撞测试以及碰撞响应的方法,绘制其实可以忽略。
- 为了方便,代码是在微信小游戏上运行的。文章结尾有本文中的示例代码,是以共享小程序片段形式给出来的,所以要运行本文示例需要安装微信开发者工具。
质点和圆形
质点定义1:“质点就是有质量但不存在体积或形状的点,是物理学的一个理想化模型。在物体的大小和形状不起作用,或者所起的作用并不显著而可以忽略不计时,我们近似地把该物体看作是一个只具有质量而其体积、形状可以忽略不计的理想物体,用来代替物体的有质量的点称为质点”。既然不考虑其形状,那么就不需要考虑其转动,而只要关注它的线性运动即可。
想象一下,我们在绘制的时候,如果不考虑转动,那么我们可以将一个圆形看作一个质点。以下我们将会用一个一个的圆形来代表质点,并模拟他们的运动。
绘制一个移动的圆形
Canvas 2d的context提供了一个方法:arc(x,y,radius,startRadian,endRadian),专门用于绘制一段正圆形的弧,参数含义:
x,y表示的是正圆形的圆心坐标radius表示半径startRadian,endRadian表示弧形开始的弧度以及结束的弧度
一个完整的圆形只要将起始弧度设置为0,终止弧度设置为2π即可。弧度和角度的换算如下:弧度=角度*180/π
根据这个方法,我们配合requestAnimationFrame即可在canvas绘制出一个可以移动的圆形,这是game.js代码:
const PI = Math.PI;
let deltaX, deltaY;// 圆形移动坐标增量
deltaX = deltaY = 1;
// 圆形的圆心坐标以及半径
let x = 0;
let y = 0;
let radius = 30;
let ctx = wx.createCanvas().getContext('2d');
// 绘制一个圆
function drawCircle(ctx, x, y, radius) {
ctx.save();
ctx.strokeStyle = 'red';
ctx.beginPath();
ctx.arc(x, y, radius, 0, 2 * PI);
ctx.closePath();
ctx.stroke();
ctx.restore();
}
// 循环绘制
function repeatDraw() {
ctx.clearRect(0, 0, ctx.canvas.width, ctx.canvas.height);
drawCircle(ctx, x, y, radius);
x += deltaX;
y += deltaY;
requestAnimationFrame(repeatDraw);
}
repeatDraw();
运行后会得到以下结果:
速度,加速度和位置
我们一起温习一下中学物理的匀加速运动:
定义物体的速度为 V ( t i ) V(t_i) V(ti),在 t i + 1 t_{i+1} ti+1时间点,那么我们的速度为 V ( t i + 1 ) V(t_{i+1}) V(ti+1),如果加速度为 a a a,则:
d t = t i + 1 − t i V ( t i + 1 ) = V ( t i ) + a / d t dt = t_{i+1} - ti\\ V(t_{i+1}) = V(t_i) + a/dt dt=ti+1−tiV(ti+1)=V(ti)+a/dt
这里的 V V V是一个向量,应该写成 V ⃗ \vec V V,因为我们现在讨论的是二维,所以可以看成 V ⃗ : [ V x , V y ] \vec V: [V_x,V_y] V:[Vx,Vy],即 V ⃗ \vec V V由 V x , V y V_x,V_y Vx,Vy组成。
我们再定义物体的位置为: P ( t i ) P(t_i) P(ti),则 t i + 1 t_{i+1} ti+1时间点的物体位置 P ( t i + 1 ) P(t_{i+1}) P(ti+1):
P ( t i + 1 ) = P ( t i ) + V ( t i + 1 ) d t P(t_{i+1}) = P(t_i) + V(t_{i+1}) dt P(ti+1)=P(ti)+V(ti+1)dt
P P P由坐标 X , Y X,Y X,Y组成。
我们看看如何用代码套用上面的公式来计算速度、加速度以及位置:
圆形的位置是由其圆心决定的,所以圆心坐标(x,y)就是公式里的 P P P。
我们在每次刷新到来之前都会重新计算圆心坐标,就像上面代码里写的:x += deltaX; y += deltaY;,如果套用上面的公式,那实际上应该是这么写:
// currentVx表示当前时间的x方向的速度
// deltaTime表示从上个速度变化到这次速度的时间
x = x + currentVx*deltaTime;
y = y + currentVy*deltaTime;
因为我们在绘制过程中是按照刷新次数来代替时间的(刷新之间间隔大约16毫秒,我之前文章有讲到),每次刷新之间的间隔都为1,也就是说这个deltaTime就是1,所以上面的代码其实应该这么写:
// currentVx表示当前时间的x方向的速度
x = x + currentVx;
y = y + currentVy;
同理currentVx和currentVy的计算可以这么写:
// currentVx表示当前时间的x方向的速度
let ax = x轴的加速度
let ay = y轴的加速度
currentVx = currentVx + ax; // 因为deltaTime为1
currentVy = currentVy + ay;
现在我们新建一个类:Vector2.js,该类描述了一个二维向量,并实现了向量的加法和减法,以及和标量的乘法,还有向量之间的点乘和叉乘。
let _value = Symbol('二维向量值的数组,0位是x,1位是y');
export default class Vector2 {
constructor(x, y) {
this[_value] = new Float32Array(2);
this.x = x;
this.y = y;
}
.......
//这里是一些属性设置,比如x,y
.......
get magnitude() {
return Math.sqrt(this.x * this.x + this.y * this.y);
}
static normalize(out, vector) {
let magnitude = vector.magnitude;
if (magnitude == 0) {
out.x = 0;
out.y = 0;
return out;
}
out.x = out.x / magnitude;
out.y = out.y / magnitude;
return out;
}
static add(out, v1, v2) {
out.x = v1.x + v2.x;
out.y = v1.y + v2.y;
}
static sub(out, v1, v2) {
out.x = v1.x - v2.x;
out.y = v1.y - v2.y;
}
static multiply(out, value) {
out.x *= value;
out.y *= value;
}
static div(out, value) {
this.multiply(out, 1 / value);
}
static dot(v1, v2) {
return v1.x * v2.x + v1.y * v2.y;
}
static cross(v1, v2) {
return v1.x * v2.y - v1.y * v2.x;
}
}
向量的叉乘实际上返回的应该一个向量而不是标量,可二维向量正好算出来只有一个值,所以这里的叉乘返回的只是一个标量而已。
现在我们就可以用这个类来表示速度以及加速度了,重新写之前的代码:
import Vector2 from "./example1208/Vector2";
const PI = Math.PI;
//实际位置算不上真正的向量,所以我们不用Vector2来表示它
let position = {x:0,y:0};
let velocity = new Vector2(1,1);
let a = new Vector2(0,0);//我们加速度为0
let radius = 30;
let ctx = wx.createCanvas().getContext('2d');
// 绘制一个圆
function drawCircle(ctx, x, y, radius) {
ctx.save();
ctx.strokeStyle = 'red';
ctx.beginPath();
ctx.arc(x, y, radius, 0, 2 * PI);
ctx.closePath();
ctx.stroke();
ctx.restore();
}
// 循环绘制
function repeatDraw() {
ctx.clearRect(0, 0, ctx.canvas.width, ctx.canvas.height);
drawCircle(ctx, position.x, position.y, radius);
Vector2.add(velocity,velocity,a);// 计算此刻的速度,相当于:v = v + a;
Vector2.add(position,position,velocity); //计算此刻的位置,相当于:x = x + vx;
requestAnimationFrame(repeatDraw);
}
repeatDraw();
我们还可以给加速度设置一些值,让这个圆形做变速运动。
如果给一个初速度 V = [ V x , 0 ] V = [V_x,0] V=[Vx,0],再模拟一个重力加速度 a = [ 0 , a y ] a = [0,a_y] a=[0,ay]即可模拟一个平抛运动。
碰撞判定
质点是没有大小的,所以这里我们如果讨论质点的碰撞判定是没意义的。但我们用正圆形来代替了质点,那就可以进行讨论了。
一个多边形,比如一个矩形,我们在碰撞判定的时候要考虑到它的4个顶点位置,同一个位置的同一个矩形,旋转角度不同判定结果也不同,有可能接触,也有可能没接触。而正圆形不管以什么角度、位置和其他的点、线接触其实都一样,我们只需要计算圆心和需要碰撞的参考物之间距离就可以判定是否接触。
正圆形碰撞其实也算到了多边形的碰撞范畴中,但我们常把其他多边形之间碰撞和圆形分开:圆形 vs 圆形,圆形 vs 多边形,多边形 vs 多边形。
其中多边形 vs 多边形的碰撞判定较为复杂,常用的有SAT和GJK判定算法,而这两个算法并不适用于圆形。
圆形和线段碰撞判定
我们学几何的时候知道:一个点到线的垂直距离最短。如果一个圆形的圆心到某条线的距离小于了圆形的半径,我们就可以认为这个圆形和这条线发生了接触。
可是如果是线段就要加上另外的判断条件了,因为线是无限长的,而线段是有限的,有可能圆到线的距离已经小于了半径,但是圆却在线段两端外,没有和线段接触。所以圆形和线段的碰撞分成两部分:
- 如果圆心到线段所在直线的投影坐标在线段外,检测圆心到线段端点的距离是否小于半径
- 如果圆心到线段所在直线的投影坐标在线段内,检测这段距离是否小于半径
计算出圆心到线段所在直线的投影点坐标是关键,我们注意到,计算圆心到直线的距离,其实就是计算圆心到投影点之间的距离,另外,我们还要计算圆心到端点距离,所以我们只需要做到:1. 计算出投影点的坐标位置;2. 实现一个方法能计算出点到点的距离。完成这两步就可以判断圆形是否和线段接触了。
投影点坐标的计算
通常我们可以根据直线斜率方程来计算出投影坐标,设线段所在直线方程为 y = k x + b y = kx+b y=kx+b,线外一点 p p p到该线段的投影点为 p 1 p_1 p1,这两点的连线必垂直于直线 y = k x + b y = kx+b y=kx+b,即可得出该直线的斜率一定是 k − 1 k^{-1} k−1,然后因为 p 1 p_1 p1一定在这两条直线上,再联立求解什么的即可得到 p 1 p_1 p1的坐标值。
我们不用这个方法,而用向量来求出该坐标。
设圆心为 p p p,线段上两个端点的坐标分别是 a a a和 b b b,那么向量 V ⃗ a p = p − a \vec V_{ap} = p - a Vap=p−a,向量 V ⃗ a b = b − a \vec V_{ab} = b - a Vab=b−a,向量 V ⃗ a p \vec V_{ap} Vap和向量 V ⃗ a b \vec V_{ab} Vab之间的夹角为 θ \theta θ,则向量 V ⃗ a p \vec V_{ap} Vap在向量 V ⃗ a b \vec V_{ab} Vab的投影长度(称为向量 V ⃗ a p \vec V_{ap} Vap在向量 V ⃗ a b \vec V_{ab} Vab上的分量)为 ∣ V ⃗ a p ∣ c o s ( θ ) |\vec V_{ap}|cos(\theta) ∣Vap∣cos(θ),根据公式:
a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ c o s ( θ ) \vec a \cdot \vec b = |\vec a||\vec b|cos(\theta) a⋅b=∣a∣∣b∣cos(θ)
得出: ∣ b ⃗ ∣ c o s ( θ ) = a ⃗ ⋅ b ⃗ / ∣ a ⃗ ∣ |\vec b|cos(\theta) = \vec a \cdot \vec b / |\vec a| ∣b∣cos(θ)=a⋅b/∣a∣, a ⃗ / ∣ a ⃗ ∣ \vec a /|\vec a| a/∣a∣正好是 a ⃗ \vec a a的单位向量(归一化,normalize)。矢量投影长度值如果乘以单位向量即可得到矢量投影:
p r o j e c t i o n a ⃗ b ⃗ = a ⃗ ⋅ b ⃗ ∣ a ⃗ ∣ a ⃗ ∣ a ⃗ ∣ projection^{\vec b}_{\vec a} = \frac{\vec a \cdot \vec b}{|\vec a|}\frac{\vec a}{|\vec a|} projectionab=∣a∣a⋅b∣a∣a
那圆心 p p p到线段 a b ab ab的投影坐标 p 0 p_0 p0就可以这样计算获得2:
p 0 = a + p r o j e c t i o n V ⃗ a b V ⃗ a p p_0 = a + projection^{\vec V_{ap}}_{\vec V_{ab}} p0=a+projectionVabVap
a ⃗ ⋅ b ⃗ \vec a \cdot \vec b a⋅b 这个点是向量点乘运算符号。
点到点的距离
这部分比较容易,设点A为 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),点B为 ( x 1 , y 1 ) (x_1,y_1) (x1,y1),他们的距离就是:
d = ( x 1 − x 0 ) 2 + ( y 1 − y 0 ) 2 d = \sqrt{(x_1 - x_0)^2 + (y_1 - y_0)^2 } d=(x1−x0)2+(y1−y0)2
我们用代码来实现上述两个计算过程:
function getDistance(point1, point2) {
let dx = point1.x - point2.x;
let dy = point1.y - point2.y;
return Math.sqrt(dx * dx + dy * dy);
}
function getProjectionPoint(point,line){
let p = point; // 线外一点p
let a = line.p1; // 线上端点a
let b = line.p2; // 线上端点b
let ap = new Vector2(p.x - a.x,p.y-a.y);
let ab = new Vector2(b.x - a.x,b.y-a.y);
let abN = Vector2.normalize(ab,ab);//计算出ab的单位向量
let compAP = Vector2.dot(ap,abN);//点乘计算出ap在ab上分量
Vector2.multiply(abN,compAP);//ap在ab上的投影,返回值就是abN
let p0 = {x:0,y:0};
Vector2.add(p0,a,abN);
return p0;
}
测试一下:
中学数学里计算点到线的距离计算方法:
设线段所在直线方程为 A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0,某点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)到该直线的距离为:
d = ∣ A x 0 + B y 0 + C A 2 + B 2 ∣ d = \left| \frac {Ax_0+By_0+C}{\sqrt {A^2+B^2}}\right| d=∣∣∣∣A2+B2Ax0+By0+C∣∣∣∣
我们可以通过线段两个端点的坐标带入到斜率式直线方程 y = k x + b y = kx+b y=kx+b 中,联立计算出 k , b k,b k,b的值,通过距离计算公式(此时 A = k , B = 1 , C = b A=k,B=1,C=b A=k,B=1,C=b)即可得到 d d d。但要注意,计算 k k k的时候一定要考虑到平行 x x x和 y y y轴的情况哦。
最终碰撞测试实现
既然知道了投影点坐标,那就可以先计算出圆心到直线的距离,如果距离大于半径,双方肯定没有接触;如果小于半径,首先看投影点是否在线段上,如果在,则说明双方接触,接触点就是投影坐标;如果不在,计算圆心到端点的距离,该距离小于半径就算接触,接触点是线段的端点:
function collideWithPoint(center, point, radius) {
let d = getDistance(center, point);
if (d < radius) {
return point;
}
return undefined;
}
function collideWithLine(center, line, radius) {
let projPoint = getProjectionPoint(center, line);
let distance = getDistance(center, projPoint);
// 如果圆到线距离小于半径
if (distance < radius) {
// 判断投影点是否在线段上:
let maxX = Math.max(line.p1.x, line.p2.x);
let maxY = Math.max(line.p1.y, line.p2.y);
let minX = Math.min(line.p1.x, line.p2.x);
let minY = Math.min(line.p1.y, line.p2.y);
if (projPoint.x >= minX && projPoint.y >= minY &&
projPoint.x <= maxX && projPoint.y <= maxY) {
// 如果在,则接触,接触点即投影点
return projPoint;
} else {
// 如果不在,判断是不是和线段端点接触
let p = collideWithPoint(center, line.p1, radius)
if (p == undefined) {
p = collideWithPoint(center, line.p2, radius);
}
return p;
}
}
return undefined;
}
圆形和圆形碰撞判定
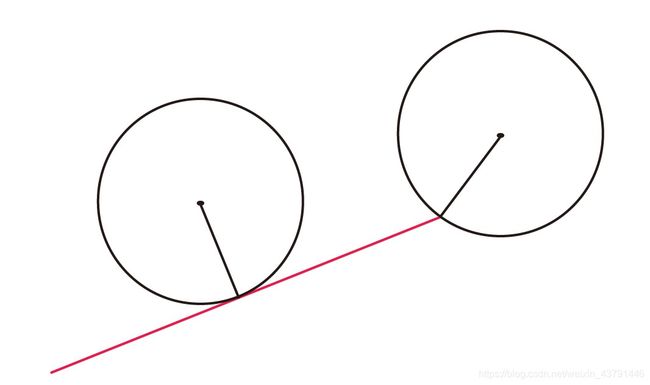
比起圆形和线段的碰撞判定,圆和圆的碰撞判定要简单得多。如果两个圆形的圆心之间的距离小于它俩的半径和,则认为两个圆形接触,接触点在两个圆心连线上,距各圆心距离分别为它们的半径。
接触点的计算我们可以根据之前给出的向量公式计算得出:
设圆A的圆心为 a a a,圆B的圆心为 b b b,则线段 a b = b − a ab = b - a ab=b−a,接触点 p p p到圆心 a a a的距离就是圆A的半径 r a r_a ra,根据上面的公式我们可以得知:
p r o j e c t i o n p ⃗ = r a a b ⃗ ∣ ∣ a b ⃗ ∣ p = a + p r o j e c t i o n p ⃗ projection_{\vec p} = r_a\frac{\vec {ab}|}{|\vec {ab}|}\\ p = a + projection_{\vec p} projectionp=ra∣ab∣ab∣p=a+projectionp
代码实现如下:
function collideWithCircle(center1, center2, radius1, radius2) {
let d = getDistance(center1, center2);
if (d < radius1 + radius1) {
// 距离小于半径和则认为两圆接触
let p = {x: 0, y: 0};
// 新建两圆心连线向量
let ab = new Vector2(center2.x - center1.x, center2.y - center1.y);
Vector2.normalize(ab, ab);// 归一化
Vector2.multiply(ab, radius1);// 计算出接触点投影向量,返回值就是ab
Vector2.add(p, center1, ab);//得到接触点坐标
return p;
}
return undefined;
}
碰撞处理
我们已经知道了如何判断圆形和线段、圆形和圆形是否接触,并且也计算出了接触点坐标位置,现在我们进行下一步处理,即碰撞后改变圆形的位置以及运动。
碰撞临界位置
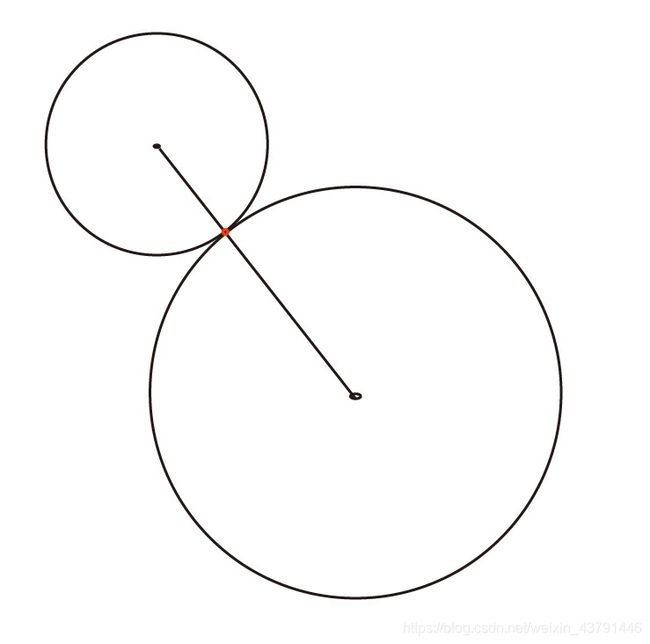
一个图形如果和另一个图形接触后,两个图形的位置是有一定重叠的。就拿圆和圆的碰撞测试来说,我们在绘制之前检测出两个圆形已经接触,这时候两个圆形其实已经相互插入了一小部分(如果速度过快会插入更深),基本上不可能正好相切。这两个圆形相互重叠的那部分距离就是两个圆形的半径和减去两个圆心的距离;如果是圆和线段碰撞,它们重叠的距离是圆半径减去接触点到圆心的距离。
插 入 深 度 圆 和 圆 = ∣ ( r a + r b ) − D i s t a n c e 两 个 圆 心 ∣ 插 入 深 度 圆 和 线 = ∣ r a − D i s t a n c e 圆 心 到 投 影 点 ∣ 插入深度_{圆和圆} = \left| (r_a+r_b) - Distance_{两个圆心}\right|\\ 插入深度_{圆和线} = \left| r_a- Distance_{圆心到投影点}\right| 插入深度圆和圆=∣(ra+rb)−Distance两个圆心∣插入深度圆和线=∣ra−Distance圆心到投影点∣
这个距离有什么用呢。如果我们让圆形朝着接触点到圆心的方向移动该距离,则圆形就会处在一个碰撞临界位置,这时候圆形和线段(或者圆形)没有碰撞,但刚刚接触上,我们称这段插入深度和接触点到圆心的方向为最小分离向量:
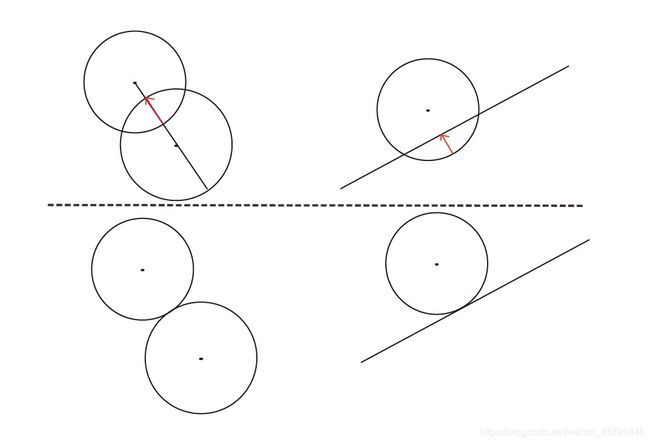
我们在代码中实现圆形运动的时候,都会在每次刷新到来时计算出它的位置并进行碰撞测试,如果圆形的位置一直处在和某个图形碰撞的位置上,那么下一次刷新到来时,我们还会检测出它俩是接触上的,然后又继续之前的计算,这就会造成错误。
一般的做法是让圆形移动到碰撞临界位置上,近似认为它是在该位置上和其他图形发生的碰撞。
这里要先明确一点,图形绘制并不是同时的,我们进行循环绘制的时候都是先计算出某图形的位置,然后进行碰撞测试,如果撞上了其他图形,那么重新给出该图形所在碰撞临界位置,最后才绘制。所以,每次我们要通过最小分离向量重新设置图形位置的时候,只需要更改相互碰撞图形中的一个即可,另一个可以认为是静止的。
例如,我有A和B两个圆形,先绘制A再绘制B,在绘制A的时候发现它和B碰上了,那就移动A,B则静止不管,当循环到绘制B的时候检测,是否和A进行过碰撞测试,测试过就跳过去,这样就不会重复计算。这里要注意,检测碰撞的时候都是用运动的图形作为检测主体,没有运动的都只作为参考,所以,如果上述中的小球A是静止的,那就没必要用它去和其他图形做碰撞测试。
小球要移到碰撞临界位置可以有两种办法:
- 直接将小球朝着分离法向量方向移动插入距离
- 朝着小球速度的反方向移动相应距离
第一种办法很容易做,但一定要确保移动小球在分离法向量的正方向上,即 V ⃗ A ⋅ n ⃗ > 0 \vec V_A \cdot \vec n > 0 VA⋅n>0。但这种方法很不好,这会让小球碰撞反弹的时候看上去很突兀,特别是在小球速度和分离向量之间的夹角很大的时候。
第二种是最好的,这需要重新计算小球的位置,设球B静止不动,球A和球B已经接触上了,则 ∣ O A − O B ∣ < R A + R B | O_A - O_B | < R_A + R_B ∣OA−OB∣<RA+RB,让 ∣ O A − O B ∣ | O_A - O_B | ∣OA−OB∣大于等于 R A + R B R_A + R_B RA+RB, O A O_A OA是通过速度和时间来计算,这样一来可以联立求出小球移动到临界位置的时间,再通过该时间和速度来确定 O A O_A OA的具值即可,然后重新计算出碰撞接触点。
运动改变
中学物理我们学过小球和小球的对心碰撞,并知道通过动量守恒和动能守恒可以计算出小球碰撞后的速度,公式好像是这样的:
m 1 v 1 + m 2 v 2 = m 1 v ’ 1 + m 2 v ’ 2 1 2 m 1 v 1 2 + 1 2 m 2 v 2 2 = 1 2 m 1 v ’ 1 2 + 1 2 m 2 v ’ 2 2 v ’ 1 = ( m 1 − m 2 ) v 1 + 2 m 2 v 2 m 1 + m 2 v ’ 2 = ( m 2 − m 1 ) v 2 + 2 m 1 v 1 m 1 + m 2 m_1v_1 + m_2v_2 = m_1v’_1 + m_2v’_2\\ \frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2=\frac{1}{2}m_1v’_1^2+\frac{1}{2}m_2v’_2^2\\ v’_1 = \frac{(m_1-m_2)v_1+2m_2v_2}{m_1+m_2}\\ v’_2 = \frac{(m_2-m_1)v_2+2m_1v_1}{m_1+m_2}\\ m1v1+m2v2=m1v’1+m2v’221m1v12+21m2v22=21m1v’12+21m2v’22v’1=m1+m2(m1−m2)v1+2m2v2v’2=m1+m2(m2−m1)v2+2m1v1
这种方法比较适合速度在同一方向上的碰撞,如果两个大小不同的球以不同的速度方向碰撞呢?
用上面公式也是可以算的:先把速度朝圆心和接触点方向以及它的垂直方向分解成两个速度,平行碰撞切线的速度不参与计算,碰撞线上的速度可以套用上面的那个公式计算出新的速度,然后新得到的速度再和平行碰撞切线的速度合成。如下图所示:
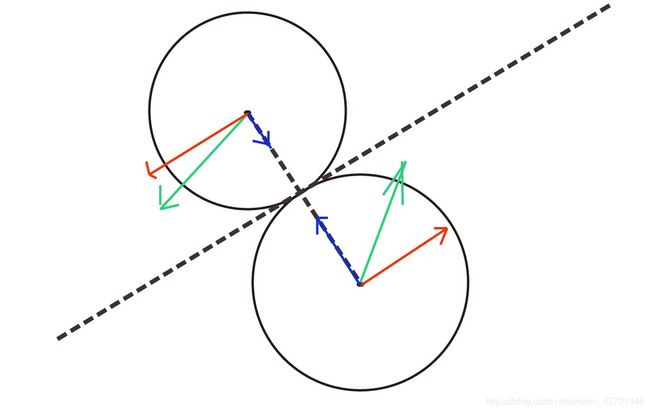
绿色表示小球的当前速度,蓝色表示该速度在碰撞方向上的分量,这个速度就可以需要通过上述公式进行计算获得新的速度,而红色分量是平行碰撞切线的,小球在这个方向上没有相互作用,则这个速度不需要计算,但它需要和蓝色速度计算出的新结果进行合成,得到小球的新的速度。但这样做很麻烦,也不好计算。
我这里用另外一个公式来计算,而这个公式是可以推导出刚体运动的碰撞响应速度公式的,只不过该公式没有加入角速度而已。在维基百科上可以找到该公式以及推导过程。
以下提到的速度等都是向量,为简化没有用向量符号表示
设物体 a a a的碰撞前速度为 V a i n V_a^{in} Vain,质量为 M a M_a Ma,物体 b b b的碰撞前速度为 V b i n V_b^{in} Vbin,质量为 M b M_b Mb。
我们认为两个物体碰撞的瞬间会产生一个很大力,且时间特别短,足以在瞬间改变两个物体的速度(力是需要时间累积才能改变物体运动的,所以我们需要一个新的量,足以在极短时间内改变速度)。我们定义一个冲量 j j j和碰撞法向量 n n n表示为: j n jn jn。
则物体 a a a和 b b b在碰撞后的速度是(公式1):
V a o u t = V a i n + j M a n V b o u t = V b i n − j M b n V_a^{out} = V_a^{in} + \frac{j}{M_a}n\\ V_b^{out} = V_b^{in} - \frac{j}{M_b}n\\ Vaout=Vain+MajnVbout=Vbin−Mbjn
只要知道 j j j的值,我们就能算出碰撞后的物体速度。
通过一系列推导可以计算出 j j j(公式2):
j = − ( 1 + e ) ( V a i n − V b i n ) ⋅ n n ⋅ n ( M a − 1 + M b − 1 ) j = \frac{-(1+e)(V_a^{in} - V_b^{in})\cdot n}{n \cdot n(M_a^{-1} + M_b^{-1} )} j=n⋅n(Ma−1+Mb−1)−(1+e)(Vain−Vbin)⋅n
将 j j j的值带入到公式1中,即可算出物体碰撞后的速度 V o u t V^{out} Vout。
这里的 e e e被称为恢复系数(The coefficient of restitution,具体怎么翻译我不知道,请懂的朋友告知),如果这个 e e e的值为1,则认为是完全弹性碰撞(我们可以通过设置 e e e的值来模拟出能量损失后的碰撞结果)。
n n n是碰撞法线,它是一个单位向量哦,其实就是圆心和接触点的连线,方向指向圆心,也就是上一节中所说的最小分离向量归一化。
如果有兴趣的话,你可以试着这样做:设 e = 1 e=1 e=1, n = [ 1 , 0 ] n = [1,0] n=[1,0](即只在x轴上碰撞),再将速度 V b i n , V a i n V_b^{in},V_a^{in} Vbin,Vain的y值设为0,即 [ V a x , 0 ] , [ V b x , 0 ] [V_{ax},0],[V_{bx},0] [Vax,0],[Vbx,0],带入到公式中算出 j j j,然后再把 j j j带回公式1中计算 V o u t V^{out} Vout,你会得到本节一开始给出的中学物理的完全弹性碰撞速度公式。
这个公式没有加入角速度,所以算我们圆形碰撞后的速度足够了。
记住这个公式,日后你会发现它和刚体碰撞的速度计算公式特别像。
最后我们用代码配合公式实现圆形碰撞后速度计算:
function collisionResponse(v1, m1, v2, m2, n, e) {
if (e == undefined) e = 1; // 恢复系数默认为1
let inverseM1= undefined;
let inverseM2= undefined;
if (m1 == Infinity) {
inverseM1 = 0;
}else{
inverseM1 = 1/m1;
}
if (m2 == Infinity) {
inverseM2 = 0;
}else{
inverseM2 = 1/m2;
}
let up = 0 - (1 + e);
let v12 = new Vector2(v1.x - v2.x, v1.y - v2.y);
up = up * Vector2.dot(v12, n);
let tempVector = new Vector2(n.x, n.y);
Vector2.multiply(tempVector, (inverseM1 + inverseM2 ));
let down = Vector2.dot(n, tempVector);
let j = up / down;
tempVector.x = n.x;
tempVector.y = n.y;
Vector2.multiply(tempVector, j * inverseM1 );
let newV1 = {x: 0, y: 0};
Vector2.add(newV1, v1, tempVector);
tempVector.x = n.x;
tempVector.y = n.y;
Vector2.multiply(tempVector, j * inverseM2 );
let newV2 = {x: 0, y: 0};
Vector2.sub(newV2, v2, tempVector);
return {newV1: newV1, newV2: newV2};
}
至此我们就已经完成了碰撞测试以及碰撞响应处理,剩下的就是写代码了,力气活儿就不多讲了,下图是示例demo:
(用微信开发者工具导入后即可看到示例源代码,还能运行。有bug自行修改)。
小结
本文我们模拟了质点运动,知道了什么是最小分离向量以及一个基于冲量的碰撞响应公式(仅有线速度),这两个概念在以后刚体运动模拟的时候还会用到。
质点运动不复杂,实现也很简单,而且很多地方可以用得上,比如二维的台球游戏啊,或者打方块的游戏啦,都可以用质点运动模拟来实现。
下一篇文章打算讲讲webgl了,如果有缘的话我们会再见的。下面二维码是我做的一个打泡泡的小游戏,就是基于质点运动模拟的,你可以玩一玩提提建议和意见:
百度百科:质点 ↩︎
维基百科:Distance from a point to a line ↩︎