汉诺塔问题：递归算法原理梳理

初学编程，接触汉诺塔递归算法
一开始就给我搞蒙了。
虽然以前有接触过汉诺塔，但是从编程的角度思考确实是第一回。
相信有很多刚接触编程的小伙伴跟我一样，看到这个解汉诺塔的递归算法以后
心里都是"WTF???"

经过一番苦思冥想，我终于算是找到了一点规律，在此总结
希望能够帮到一些跟我一样刚入门的朋友
同时也给自己做一个备查的记录
OK，开始正题

---

汉诺塔问题描述

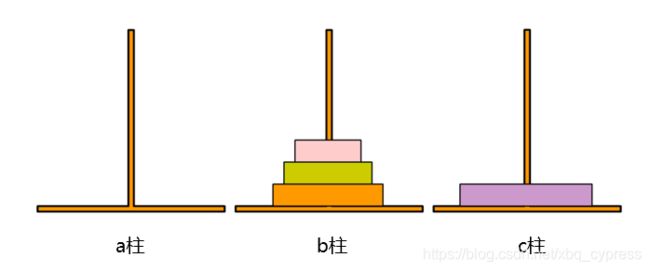
1. 有三根柱子，在其中一个柱子上，从上到下套着N个从小到大的盘子
2. 要求把左边所有的盘子移动到右边
3. 每次只能移动一个盘子
4. 大盘子不能放置在小盘子之上

如图所示
需要将左侧的盘子，按照大的在下，小的在上的规则，全部移动到右侧（如下）

汉诺塔递归代码

因为我学的是python，所以这里写的是python代码

def hanoi(n,a,b,c):#定义函数 名称 hanoi 意图 将a柱的 n个盘子 移动到c柱
	if n == 1:
		print(a,'-->',c) 
	else:
		hanoi(n-1,a,c,b) #把n-1个盘子，从a柱移动到b柱
		hanoi(1,a,b,c)   #移动第n个盘子，从a柱到c柱
		hanoi(n-1,b,a,c) #将b柱的n-1个盘子，移动到C柱
n=int(input('请输入层数：'))
hanoi(n,'tower1','tower2','tower3')

逻辑分析

这个问题我们可以简单类比为

把大象放进冰箱需要几步：

1. 打开冰箱
2. 把大象放进去
3. 把冰箱门关上

把a柱的n个盘子移动到c柱需要几步：

1. 把前n-1个盘子都移动到b柱
2. 把最大的盘子（第n个）移动到c柱
3. 把b柱上的n-1个盘子移动到c柱
   如下
   
   
   
   当n=1的时候，直接从a柱移动到c柱。

推导过程中的问题

很多同学可能会说
你说的这个逻辑我可以理解
但是为什么hanoi函数里
要用hanoi(n-1,a,c,b)
还有hanoi(n-1,b,a,c)
这都代表什么意思呢？
ok，现在我从自上而下的逻辑角度，还有自下而上的细节角度来解释这个问题

逻辑层(自上而下)

在这里，要明确一个概念，就是型参与实参
这也是为什么在代码中
实参输入的是tower1,tower2,tower3
而函数的形参我用a,b,c来定义
就是为了让大家更好的区分

如果不了解形参和实参的同学，可以去查一下资料

OK，了解了形参与实参，我们自上而下分析这段代码
首先我们假设，我们 def 一个函数 hanoi(n.a.b.c)
这个函数的作用是将a上的n个盘子全部移动到c （注意这里是形参）

hanoi 函数的逻辑内核是什么呢？（以下将hanoi简称h函数）
h(n,a,b,c):
if n =1:
a --> c
h1(将a上前n-1个盘子,从a移动到b)
h0(将a上第n个盘子,从a移动到c）
h2(将b上的n-2个盘子,从b移动到c)
(h0,h1,h2都是h函数，只不过参数不同)

假设h函数成立，只要证明h1,h0,h2是可以成立的，就可以反证h函数成立

怎么证明呢？以h1为例

假设h函数的实参是(n,tower1,tower2,tower3)

独立来看，在 h1(n,a,b,c) （我们先假定此时h1的参数与h函数还未建立关联）中

想把tower1上的n-1个盘子，移动到tower2
需要怎么做？
首先 形参 n 带入的 实参 是 n-1
其次 形参 a 带入的 实参 是 tower1
然后 形参 b 带入的 实参 是 tower3
最后 形参 c 带入的 实参 是 tower2

推导到这里，我们希望，将实参带入的时候，h1的形参设定，能够按照上面的规则赋值，我们再回头看下逻辑

h(n,a,b,c):
if n =1:
a --> c
h1(将a上前n-1个盘子,从a移动到b)
h0(将a上第n个盘子,从a移动到c）
h2(将b上的n-2个盘子,从b移动到c)

综上
h1 在 h 中的参数设定 为(n-1,a,c,b) #将a上前n-1个盘子,从tower1移动到tower2（此处b的值等于h函数中b的值）

然后再看公式，是不是就可以理解为什么中间这么设置了

后面的h0,h2就不做推论

def hanoi(n,a,b,c):#定义函数 名称 hanoi 意图 将a柱的 n个盘子 移动到c柱
	if n == 1:
		print(a,'-->',c) 
	else:
		hanoi(n-1,a,c,b) #把n-1个盘子，从a柱移动到b柱
		hanoi(1,a,b,c)   #移动第n个盘子，从a柱到c柱
		hanoi(n-1,b,a,c) #将b柱的n-1个盘子，移动到C柱
n=int(input('请输入层数：'))
hanoi(n,'tower1','tower2','tower3')

推演层(自下而上)

将n=1 n=2 n=3的情况分别带入



带入后，会发现，正是我们之前所预料的那样，除了n=1的时候之外，其他的时候，h1,h0,h2的步骤都是全的

然后我们看到n=3的时候，去看h1
他的h1其实就跟n=2的时候一样

如果还不好理解
可以将 a,b,c用 起始柱，中转柱，目标柱来代替（这里都是形参）
n=3的 h1 其实就是 n=2 的h函数 不过目标柱是 tower2

总结

汉诺塔的递归算法，是递归算法的代表。
在我的理解（刚开始学习，愚见，如果有错误还请各位指证）

一、递归算法有两个要点
1 找到一个普规律，定义函数，然后调用自己的n-1，n-2之类
2 有一个算法内核，这个内核可能是 n=1的时候的算式，可能是n=2的时候

在汉诺塔中

定义普遍规律“大象放冰箱”—>“开门”---->“放大象”----->“关门”

算法内核有两个
1.n=1的时候 直接移动
2.n=2的时候 是 “大象放冰箱” 的全过程的最简版本
二、目标柱与中转柱的不断换位，导致当n不同时，第一步走向