『算法』如何用链表从 0 开始实现一个 LRU 缓存

阅读本文仅需 5 分钟

常把编程比作习武，受到了一点金庸老爷子的武侠影响。

编程语言是武器，数据结构与算法是内功心法，网络，操作系统，组成原理等是基本功。各种技术是各式各样的武功路数。内功心法和基本功掌握的程度制约着我们能走的多远，能学到多深多强的技术。

武功之深，在于内功心法的深厚。因此万千变化的世界，我们要学着修炼自己的内功心法。

今天在此开辟一个专题模块，系统地讲述数据结构与算法相关知识。层层递进，不缺斤少两。

为什么我要选择一整个专题模块来写这里的内容呢？

就我个人而言，我觉得我的时间基本被移动互联网碎片化了，第一，找到一整块大量的时间很难，其次，一下子学太多了，也消化不了，再次，碎片化学习让我们陷入浅思考状态，殊不知有很多东西是需要我们去深入思考的，这就很容易陷入一个弊端：就是这个好像我会，然后一上手做，发现好像又不会。但是碎片化时间不利用一下又觉得亏，所以我觉得我们的碎片化时间需要合理利用一下，用来学一套系统的东西其实是很好的。平时在各大公号各大技术平台都能星星点点看到些有用的内容，我曾经也吃过这的苦头，学的很不痛快，看到某个地方，突然没了，或者某些东西突然断了。。。所以开个模块，一篇一篇递进，不缺斤少两，专门讲数据结构和算法。希望能带给大家一些帮助。

先开个篇：
给几个概念：
数据结构与算法的定义：
简单点讲：数据结构即使一组数据的存储结构，算法就是操作数据的一组方法。

下面数据结构与算法所需要掌握的相关内容，可以了解一下。

既然算法是操作数据的一组方法，那么这些方法必定有优劣之分，如何衡量一个算法的好坏呢，这里引入新的概念，复杂度。

• 时间复杂度：表示算法的执行时间与数据规模之间的增长关系。
• 空间复杂度：算法的存储空间和数据规模之间的增长关系。

一个算法衡量一般从几个角度来分析：

• 最好，最坏情况时间复杂度
• 平均时间复杂度：加权平均时间复杂度或者叫做期望时间复杂度
• 均摊时间复杂度：把耗时多的那一次操作均摊到耗时少的上面。

数组

数组大概就是最基本的一种数据结构了吧。虽然它很基础，但是这里我还是将它介绍一下，以便于为后面内容的展开。

数组是一种线性数据结构，它用一组连续的内存空间来存储一组具有相同类型的数据。

链表

链表：不需要一块连续的内存空间，通过指针将一组零散的内存块串联起来使用。

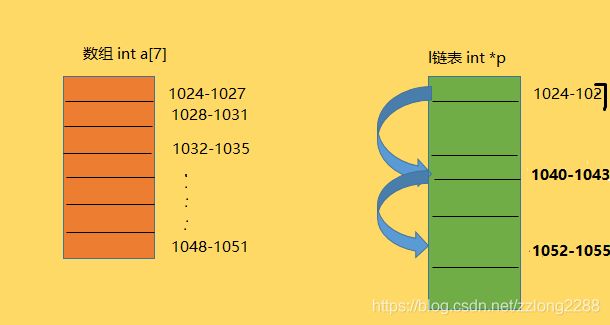
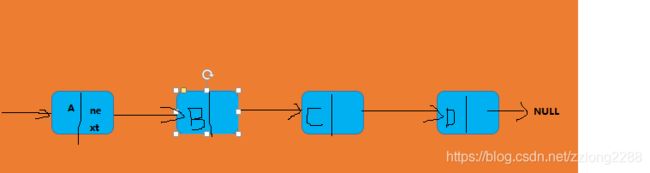
• 单链表
  从图中大致可以看出，头结点和尾结点比较特殊，头结点用来记录这个链表的基地址，我们通过头结点就可以遍历得到整个链表了。尾结点指向的是一个空地址 NULL，表示最后一个结点。
  上面的数组可以看到，一旦我们进行插入删除，由于内存的连续性，我们需要对大量的数据进行移动，而链表则不需要，只需要改变某个（些）结点的指针指向就可以了。

• 链表的插入
  

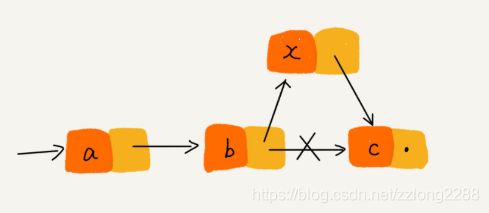
 ptr -> data = x;
 ptr -> next = b->next;
 b->next = ptr;

• 链表的删除
  

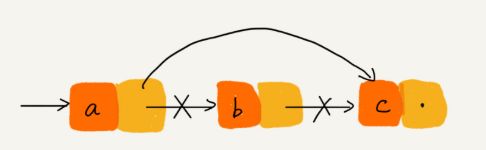
temp = a -> next; // 将 b 结点信息暂存
 a -> next = temp -> next; // 执行删除
 delete temp;   // 注意C/C++ 需要释放指针

循环链表，和单链表相比，循环链表的优点就是尾结点指向了头结点。
双向链表
顾名思义：双向链表有两个方向：即每个结点都会用两个指针，一个用来存储后一个结点的地址的 next 指针，另一个用来存储前一个结点的地址的 prev 指针。

时间复杂度比较

\时间复杂度\	数组	链表
插入	O(n)	O(1)
删除	O(n)	O(1)
随机访问	O(1)	O(N)

常用算法

结合代码看一下链表的一些基本操作，同时对一些经典的算法（面试常考的算法）做一些解释
由于单链表实现最简单，功能最少，所以最具有操作性，所以以下，均以单链表做示例。

/**
 * 1) 单链表反转
 * 2) 链表中环的检测
 * 3) 两个有序的链表合并
 * 4) 删除链表倒数第 n 个结点
 * 5) 求链表的中间结点
 */
 /** 链表结点定义 **/
 typedef struct SingleLinkedNode {
     int data;
     struct SingleLinkedNode* next;
 } SingleLinkedNode;
 /** 插入结点 **/
 void insertNode(SingleLinkedNode** head_ref, int data);
 /** 反转单链表 **/
 void reverse(SingleLinkedNode** head_ref){
    if(*head_ref == NULL) return;
    SingleLinkedNode *prev = NULL;
    SingleLinkedNode *current = *head_ref;
    while(current) {//当当前指针不为空，执行循环
        SingleLinkedNode *next = current->next;
        if(!next) { //如果当前指针的下一个指针为空，即当前指针为尾结点
            *head_ref = current;//将尾结点地址存入头结点中
        }
        current->next = prev;
        prev = current;
        current = next;
    }
 }

 /** 环的检测 **/
 int checkCircle(SingleLinkedNode** head_ref)
 {
     if(*head_ref == NULL) return 0;
     // 快慢指针解决环的问题
     SingleLinkedNode *slow = *head_ref;
     SingleLinkedNode *fast = *head_ref;
     while(fast != NULL && fast -> next != NULL){
         fast = fast->next->next;
         slow = slow -> next;
         if(slow == fast){
             // 有环，返回1
             return 1;
         }
     }
     return 0;
 }
 void moveNode(SingleLinkedNode** dest_ref,SingleLinkedNode** src_ref);
 /** 两个有序链表合并 **/
 SingleLinkedNode* mergeSortedLinkedList(SingleLinkedNode* list1, SingleLinkedNode* list2){
     //辅助结点,next 指针持有合并后的有序链表
     SingleLinkedNode temp;
     // 有序链表的尾结点
     SingleLinkedNode* tail = &temp;
     while(1){
         // 如果有一个链表为空，直接与另一个链表链接起来
         if(!list1){
             tail->next = list2;
             break;
         } else if(!list2)
         {
             tail -> next = list1;
             break;
         }
         //将头结点较小的优先添加到 tail
         if(list1->data <= list2->data){
             moveNode(&(tail->next),&list1);
         } else {
             moveNode(&(tail->next),&list2);
         }
         tail = tail -> next;

     }
     return temp.next;
 }

 /** 移动结点 **/
 void moveNode(SingleLinkedNode** dest_ref,SingleLinkedNode** src_ref){
     if(*src_ref == NULL) return;
     SingleLinkedNode* new_node = *src_ref;
     *src_ref = new_node -> next;
     // 目的结点接到新节点后面
     new_node->next = *dest_ref;
     *dest_ref = new_node;
 }

 /** 删除倒数第k个结点 **/
 void deleteLastKth(SingleLinkedNode** head_ref,int k){
     if(*head_ref == NULL) return ;
     SingleLinkedNode* fast = *head_ref;
     // fast 指针先走 k 步
     int i = 1;
     while(fast != NULL && i < k){
         fast = fast -> next;
         i++;
     }
     // 此处判断一下，fast 指针是否走了 K 步，即判断 fast 指针是否指向空，若为空，则表示链表元素个数小于k
     if(fast == NULL) return ;

     SingleLinkedNode* slow = *head_ref;
     SingleLinkedNode* temp = NULL;  //临时结点,保存 slow 结点的前一个结点，即哨兵结点避免对头和尾结点特殊处理
     while(fast -> next != NULL){
         fast = fast -> next;
         temp = slow;
         slow = slow -> next;
     }
     // 如果 temp（头结点的前一个结点） 为空，说明头结点刚好为第 k 个结点,则表明要删除的是头结点，则需要将头结点的下一个节点的地址存到头结点上，并释放掉头结点
     if(!slow){
         *head_ref = (*head_ref)->next;
     } else {
         // 将 slow 结点的 next 指针存到 slow 的前一个结点上的 next 上
         temp -> next = slow -> next;
     }
     free(slow);  // 释放掉 slow 指针
 }

 /** 求中间结点 **/
 SingleLinkedNode* findMiddleNode(SingleLinkedNode* head){
     SingleLinkedNode* fast = head;
     SingleLinkedNode* slow = head;
    // 用快慢指针即可解决，快指针速度是慢指针两倍，当快指针走完，即可得到慢指针正好到中间结点位置
     while(fast->next != NULL && fast->next->next != NULL) {
         slow = slow -> next;
         fast = fast -> next -> next;
     }
     return slow;
 }
 /** 插入新结点到链表头部 **/
 void insertNode(SingleLinkedNode** head_ref,int data){
     SingleLinkedNode* new_node = malloc(sizeof(SingleLinkedNode));  // 新建一个结点
     new_node -> data = data;
     new_node -> next = *head_ref;
     *head_ref = new_node;
 }

由于篇幅有限，测试方法以及整个源代码，可点击「阅读原文」查看。

应用

基于一些高速存储器空间通常是比较稀缺的，但是他们又和硬盘读取速度相差太大，所以导致读取的效率非常慢，这里我们就考虑用到缓存，可以实现更高性能地读取数据，同时由于缓存空间有限，所以我们需要设计一些淘汰算法来优化空间的使用，LRU 缓存算法就是其中一个，常见的缓存算法有

• FIFO：先进先出算法，使用队列的方式，淘汰最先进来的数据
• LFU：最少使用算法，淘汰最少的使用的数据
• LRU：最近最少使用算法，淘汰最近没有用过的数据

这里我们用单链表实现一个简单的 LRU 缓存算法，加深对单链表的理解的同时也能对 LRU 缓存算法有一定的了解。

LRU 算法：
最近使用得最少的就淘汰。使用链表可以如下实现：
用一个单链表作为缓存空间，越靠近尾部的结点是越早访问。当有一个新的数据被访问时：
我们从头遍历链表，

• 如果此数据之前已经被缓存到链表中，则删除链表中的那个数据，并将该数据插入到头结点处。
• 如果没有遍历到该数据，则说明该数据之前没有被缓存到链表中，则进行以下操作：
  • 判断链表未满：直接将该数据插入到头结点
  • 判断链表满了：则删除尾结点，并将该数据插入到头结点
    缓存访问的时间复杂度为O(n)

typedef int DataType;
// 定义结点
class SNode
{
public:
    DataType data;
    SNode * next;
};
class SList
{
public:
    SList();
    SList(int MaxSize);
    ~SList();
    void insertElemAtBegin(DataType x);     // 头部插入结点
    bool findElem(DataType x);    // 查找x,存在则返回true，否则返回false
    void deleteElemAtEnd();    //删除尾结点
    bool deleteElem(DataType x);    // 删除指定节点，如果存在则删除，返回true，否则删除失败返回false
    bool isEmpty();    // 查看链表是否为空，true表示空
    bool isFull();    // 查看链表是否已满，true 表示不满
    void printAll();    // 打印链表元素
private:
    int MaxSize;    // 链表可以存放最大的数据
    int length;    // 链表长度
    SNode * head;    // 指向头结点
};

/**
 * 1.单链表的插入，删除，查找操作
 * 2.链表中存储的是 int 类型
 *
 */
#include 
using namespace std;

//初始化单链表
SList::SList() {
    head = new SNode;  //申请头结点
    head -> next = NULL;
    this -> length = 0;
    this -> MaxSize = 10;
}
SList::SList(int MaxSize) {
    head = new SNode;
    head -> next = NULL;
    this -> length = 0;
    this -> MaxSize = MaxSize;
}
//销毁单链表，要把开辟的空间都释放，然后再销毁
SList::~SList() {
    SNode* ptr,* temp;
    ptr = head;
    while(ptr -> next != NULL){
        temp = ptr->next;
        ptr->next = ptr->next->next;
        delete temp;
    }
    delete head; //最后删除头结点
    this->head = NULL;
    this->length = 0;
}

//链表头部插入结点
void SList::insertElemAtBegin(DataType x) {
    SNode * ptr = new SNode;
    ptr -> data = x;
    ptr -> next = head->next;
    head->next = ptr;

    this->length ++;
}
//查找x，存在则返回1，不存在则返回0
bool SList::findElem(DataType x) {
    SNode *ptr;
    ptr = head;
    while(ptr->next != NULL){
        if(ptr->next->data == x){
            return true;
        }
        ptr = ptr -> next;
    }
    return false;
}

// 删除尾结点
void SList::deleteElemAtEnd() {
    SNode * ptr ,* temp;
    ptr = head;
    while(ptr -> next != NULL && ptr -> next -> next != NULL){// 倒数第二个结点
            ptr = ptr -> next;
    }
    temp = ptr -> next;
    ptr -> next = temp -> next;
    this -> length--;
    delete temp;
}
//删除指定节点
//如果存在则删除返回true
//不存在则不删除，返回false,表示不存在该元素
bool SList::deleteElem(DataType x) {
    SNode *ptr, * temp;
    ptr = head;
   while(ptr -> next != NULL){
       if(ptr -> next -> data == x){
           temp = ptr -> next;
           ptr -> next = temp -> next;
           delete temp;
           this -> length --;
           return true;
       }
       ptr = ptr -> next;
   }
   return false;
}

// 查看链表是否为空，1表示不为空，0表示为空
bool SList::isEmpty()
{
    if(this -> length == 0){  //空
        return false;
    }
    else{
        return true;
    }
}

// 查看链表是否满，1表示不满，0表示满
bool SList::isFull()
{
    if(this -> length == this -> MaxSize){  //满
        return false;
    }
    else{
        return true;
    }
}
// 打印链表
void SList::printAll() {
    SNode *ptr;
    ptr = head;
    while(ptr -> next != NULL){
        ptr = ptr -> next;
        cout< data <<"   ";
    }
    cout << endl;
}
int main(){
    cout << "LRU 链表缓存测试： " << endl;
    SList sList(5);
    int num = 0;
    while(1){
        cout << "please enter a num,-1 EXIT" << endl;
        cin >> num;
        if(num == -1)
            break;
        if(sList.findElem(num)){  // 遍历数据是否存在
            sList.deleteElem(num);
            sList.insertElemAtBegin(num);
        }
        else {
            if(sList.isFull()){ // 链表未满
                sList.insertElemAtBegin(num);
            }
            else{  // 链表已满
                sList.deleteElemAtEnd();
                sList.insertElemAtBegin(num);
            }
        }
        sList.printAll();
    }
    return 0;
}

注意：链表使用注意事项
指针或者引用的含义：
对于指针的理解，其实这样理解就可以了：
将某个变量赋值给指针，实际上就是将这个变量的地址赋值给指针。p->next = q 其实就是将 q 的内存地址存储到了 p->next指针中了。

警惕指针丢失和内存泄露
链表代码中频繁操作指针，很容易丢失指针，当刚接触的时候可以动手画一下指针操作的图，这样可以避免我们由于考虑不周无端丢失指针。
引入哨兵结点简化头结点和尾结点的特殊处理

下文预告：栈以及栈的应用如需代码资源或者有疑问的地方可以关注我，即可获得对应详细注释的代码以及测试代码资源。