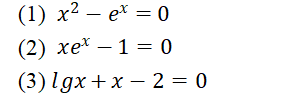非线性方程求根数值解法
非线性方程求根数值解法
一、 实验目的
（1）通过对二分法与牛顿迭代法做编程练习和上机运算，进一步体会二分法和牛顿法的不同。
（2）编写割线迭代法的程序，求非线性方程的解，并于牛顿迭代法作比较。
二、 实验内容
1、用牛顿迭代法求下列方程的根
2、编写割线法程序求解第一问的方程
三、 实验步骤、程序设计、实验结果及分析
1、牛顿迭代法
（一）若函数f（x）在点的某一邻域内具有直到（n+1）阶导数，则在该邻域内f（x）的n阶泰勒公式为：
f(x)=f(x0)+f`( x0)(x- x0)+f``( x0)(x-x0)²/2!+f```( x0)(x- x0)³/3!+...fn(x0)(x- x0)^n/n!+....
其中：fn(x0)(x- x0)^n/n!，称为拉格朗日余项。以上函数展开式称为泰勒级数。
（二） 取其线性部分，作为非线性方程f(x) = 0的近似方程，即泰勒展开的前两项，则有f(x0)+f'(x0)(x－x0)=0 。设f'(x0)≠0则其解为x1=x0－f(x0)/f'(x0) 这样，得到牛顿法的一个迭代序列：x n+1=x n －f(x n ) /f'(x n )。
2、二分法
（一）如果要求已知函数 f(x) = 0 的根 (x 的解)，那么
（二）先要找出一个区间 [a, b]，使得f(a)与f(b)异号。根据介值定理，这个区间内一定包含着方程式的根。
（三）求该区间的中点m=(a+b)/2，并找出 f(m) 的值。
（四）若 f(m) 与 f(a) 正负号相同，则取 [m, b] 为新的区间, 否则取 [a, m]。
（五）重复第三步和第四步，直到得到理想的精确度为止。
3、弦截法
任取两个数x1、x2，求得对应的函数值f(x1）、f(x2）。如果两 函数值同号，则重新取数，直到这两个函数值异号为止。连接（x1,f(x1））与（x2,f(x2））这两点形成的直线与x轴相交于一点x，求得对应的f(x），判断其与f(x1）、f(x2）中的哪个值同号。如f(x）与f(x1）同号，则f(x）为新的f(x1)。将新的f(x1）与f(x2）连接，如此循环。
4、程序设计
#include
#include
#include
/********************函数************************/
double f1(double x){ //函数f(x)
return (x*x - exp(x));
}
double f2(double x){ //函数f(x)
return (x*exp(x)-1);
}
double f3(double x){ //函数f(x)
return (log10(x)+x-2);
}
/*******************牛顿迭代*************************/
double df1(double x){ //f(x)的导数
return (2*x - exp(x));
}
double df2(double x){ //f(x)的导数
return (exp(x)+x*exp(x));
}
double df3(double x){ //f(x)的导数
return ((1/log(10))*(1/x)+1);
}
double Newton1(double x){ //牛顿迭代函数
return (x - f1(x) / df1(x));
}
double Newton2(double x){ //牛顿迭代函数
return (x - f2(x) / df2(x));
}
double Newton3(double x){ //牛顿迭代函数
return (x - f3(x) / df3(x));
}
/*****************二分法******************/
int erfenfa1(double &a,double &b){
double x0=(a+b)/2;double fx0=f1(x0);
double fa=f1(a),fb=f1(b);
if(fx0==0) return 1;
else if((fa*fx0)<0) {b=x0;return 0;}
else if((fb*fx0)<0) {a=x0;return 0;}
}
int erfenfa2(double &a,double &b){
double x0=(a+b)/2;double fx0=f2(x0);
double fa=f2(a),fb=f2(b);
if(fx0==0) return 1;
else if((fa*fx0)<0) {b=x0;return 0;}
else if((fb*fx0)<0) {a=x0;return 0;}
}
int erfenfa3(double &a,double &b){
double x0=(a+b)/2;double fx0=f3(x0);
double fa=f3(a),fb=f3(b);
if(fx0==0) return 1;
else if((fa*fx0)<0) {b=x0;return 0;}
else if((fb*fx0)<0) {a=x0;return 0;}
}
/*****************弦割法*******************/
double xiangefa1(double nu0,double nu1){
return (nu1-f1(nu1)*(nu1-nu0)/(f1(nu1)-f1(nu0)));
}
double xiangefa2(double nu0,double nu1){
return (nu1-f2(nu1)*(nu1-nu0)/(f2(nu1)-f2(nu0)));
}
double xiangefa3(double nu0,double nu1){
return (nu1-f3(nu1)*(nu1-nu0)/(f3(nu1)-f3(nu0)));
}
int main()
{
double num1,num2;//牛顿迭代初值
double a,b;int flag;//二分法初始区间
double nu0,nu1,nu2;//弦割法初值
int count; //迭代次数
double e=0.000001; //结果精度
double distance;
int i;
printf("牛顿迭代法：\n");
for (i=1;i<=3;i++){
num2=2.0;
for(count=1;count<=1000;count++){
switch(i){
case 1:num1=Newton1(num2);break;
case 2:num1=Newton2(num2);break;
case 3:num1=Newton3(num2);break;
}
//printf("%d %f\n",count,num1);
distance=fabs(num1-num2);
num2=num1;
if(distance