优先级队列PriorityQueue
在小顶堆或是大顶堆堆操作中经常会用到优先级队列PriorityQueue。网上有篇文章讲的不错,转载一波梭哈。
一、什么是优先级队列
1、概念
我们都知道队列,队列的核心思想就是先进先出,这个优先级队列有点不太一样。优先级队列中,数据按关键词有序排列,插入新数据的时候,会自动插入到合适的位置保证队列有序。(顺序有两种形式:升序或者是降序)
来一个标准点的定义:
PriorityQueue类在Java1.5中引入。PriorityQueue是基于优先堆的一个无界队列,这个优先队列中的元素可以默认自然排序或者通过提供的Comparator(比较器)在队列实例化的时排序。要求使用Java Comparable和Comparator接口给对象排序,并且在排序时会按照优先级处理其中的元素。
比如我们往队列里面插入1 3 2,插入2的时候,就会在内部调整为1 2 3(默认顺序是升序)。正是由于这个优良特性可以帮助我们实现一系列问题。我们先看一个例子,体会一下他的优点,然后再看一下为什么能够实现这样的功能。

我们看到就算是我们随意插入数据,但是输出的结果总是有序的,这样一来优先级队列就可以有了很多个使用场景。下面给出一道力扣题。体会一下他的优点。
2、案例演示特性
Leetcode215题:在未排序的数组中找到第 k个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
输入:3,2,3,1,2,4,5,5,6,k = 4。输出就是5,因此重复的并不考虑。我们一般情况下一般首先想到冒泡排序。每一次都冒出来一个最小的元素,这样冒K次,就是我们想要的结果。

其实冒泡排序还可以解决另外一个问题,那就是返回Z倒数第K大的元素,方法是每次冒出来一个最大的元素即可。
这样做很简单,但是需要我们自己手写冒泡排序,下面我们看使用优先级队列如何解决的。

就这几行代码就搞定了,是不是超级简单。为什么优先级队列能够实现呢?下面我们来分析一下他的数据结构:
3、数据结构
优先级队列底层的数据结构其实是一颗二叉堆,什么是二叉堆呢?我们来看看
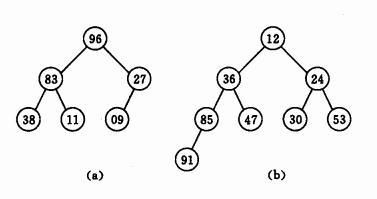
在这里我们会发现以下特征:
(1)二叉堆是一个完全二叉树
(2)根节点总是大于左右子节点(大顶堆),或者是小于左右子节点(小顶堆)。
如果我们要插入一个节点怎么办呢?
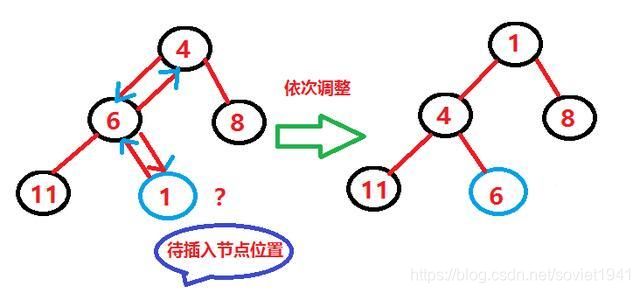
自己使用画图工具画的,能看懂就行,不要在意那些细节兄弟。过程如下:
(1)找到待插入位置:满足完全二叉树的特点,依次插入
(2)插入之后判断是否满足二叉堆的性质,不满足那就调整
(3)1<–>6交换,发现不满足,1<–>4交换,满足即停止。
对于我们的优先级队列就是这样的一种数据结构,因此我们在插入的时候保证了数据的有序性。
OK。到这基本上我们能够体会到优先级队列的思想了。来一个小结:
优先级队列使用二叉堆的特点,可以使得插入的数据自动排序(升序或者是降序)。
现在我们知道了这些,还没讲源码。从源码的角度来体会一下:
二、源码分析(基于jdk1.8)
源码分析一般的顺序都是先类属性、构造方法、普通方法。在编译器中鼠标定位到这个PriorityQueue上,ctrl+鼠标左键就可以进入到这个集合的源码里面。
1、属性
2、构造方法
(1)默认构造方法:PriorityQueue()
使用默认的初始容量(11)创建一个 PriorityQueue,并根据其自然顺序对元素进行排序。
(2)包含集合元素:PriorityQueue(Collection c)
创建包含指定 collection 中元素的 PriorityQueue。
(3)指定初始容量:PriorityQueue(int initialCapacity)
使用指定的初始容量创建一个 PriorityQueue,并根据其自然顺序对元素进行排序。
(4)指定初始容量和比较器:PriorityQueue(int initialCapacity, Comparator comparator)
使用指定的初始容量创建一个 PriorityQueue,并根据指定的比较器对元素进行排序。
(5)包含优先级元素:PriorityQueue(PriorityQueue c)
创建包含指定优先级队列元素的 PriorityQueue。
(6)包含set元素:PriorityQueue(SortedSet c)
创建包含指定有序 set 元素的 PriorityQueue。
3、普通方法
PriorityQueue中常用的方法很多。来看几个常用的。
(1)add:插入一个元素,不成功会抛出异常
public boolean add(E e) { return offer(e);}
我们看到add方法其实是通过调用offer方法实现的。我们直接看offer方法
(2)offer:插入一个元素,不能被立即执行的情况下会返回一个特殊的值(true 或者 false)
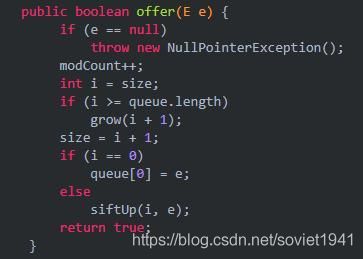
注意,优先级队列插入的元素不能为空,这一点在文章一开始提到过。步骤是这样的:
首先把modCount数量加1,如果容量不够把当前队列的尺寸加1,最后在i的位置上使用siftUp方法把e添加进来。此时真正插入的操作又落到了siftUp方法身上,我们接着看。
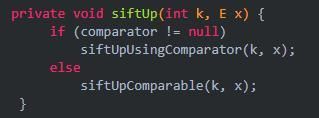
尼玛,这里也没有实现真正的插入操作,而是先判断是否使用了自己的比较器。我们直接来看自己的比较器不为空,如何插入。

这里就是真正的插入操作了。一个正常的数据插入过程。没什么特别的。
(3)remove:删除一个元素,如果不成功会返回false。
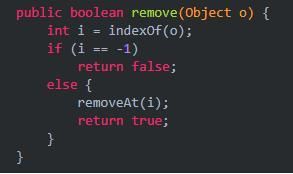
这里会发现真正实现删除操作的是removeAt方法。我们跟进去看看
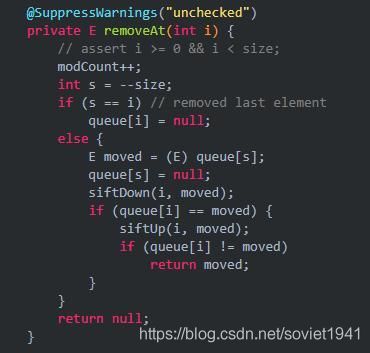
这个删除操作主要是两部分,if里面判断删除的是否是最后一个,否则的话就是用siftDown方法进行“向下沉”删除。不成功那就使用“向上浮”。

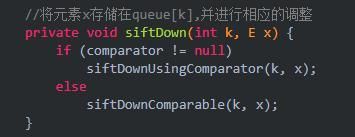
删除的时候同样需要进行判断比较器。
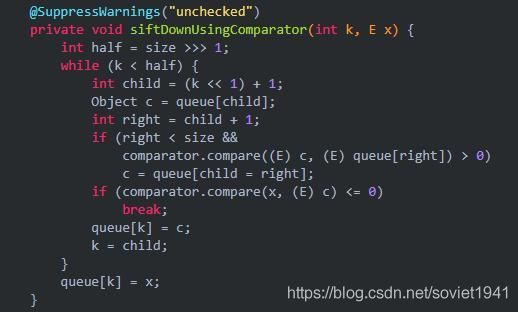
OK。删除操作就是这么多。基本思路是向上浮还是向下沉。
(4)poll:删除一个元素,并返回删除的元素

又回到了siftDown删除操作,就不赘述了。
(5)peek:查询队顶元素
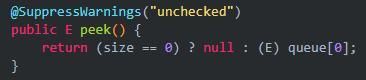
(6)indexOf(Object o):查询对象o的索引
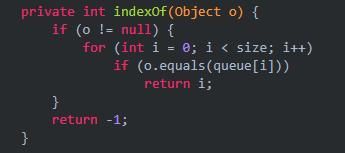
(7)contain(Object o):判断是否容纳了元素

实现原理很简单和上面的一样。
