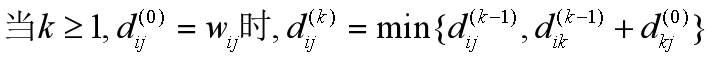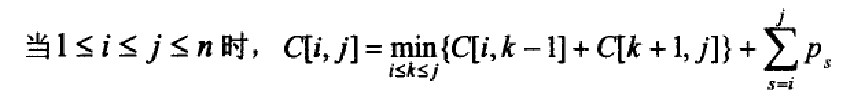算法学习之动态规划(Dynamic programming)
动态规划(Dynamic programming)
文章目录
- 动态规划(Dynamic programming)
- 基本思路
- 与分治法比较
- 斐波那契
- 计算二项式系数
- 时间效率分析
- Warshall算法
- 定义
- Floyd算法
- 最优二叉查找树
- 二叉查找树(Binary Search Tree)
- 背包问题
- 记忆功能
基本思路
- 解决若干个(交叠)子问题
- 将子问题的解用表格记录下来,避免子问题的重复计算
- 上述表格的最终状态即为(包含)最终解
与分治法比较
- 都将问题划分为若干个子问题
- 分治法中各子问题相互独立,而动态规划中各子问题允许相互交叠
斐波那契
当n>1时,F(n)=F(n-1)+F(n-2)
F(0)=0,F(1)=1
算法 Fib(n)
F[0] = 0, F[1] = 1
for i=2 to n do
F[i] =F[i-1] + F[i-2]
return F[n]
计算二项式系数
递推式
C(n, k) = C(n-1, k-1) + C(n-1, k), 当n > k >0
C(n, 0) = C(n, n) = 1
动态规划算法
- 把二项式系数记录在一张n+1行k+1列的表中
Binomial(n,k)
//用动态规划算法计算C(n,k)
//输入:—对非负整数n>=k>=0
//输出:C(n,k)的值
for i← 0 to n do
for j ← 0 to min(i,k) do
if j=0 or j=i
C[i,j] ← 1
else C[i,j] ←C[i-1,j-1]+C[i-1,j]
return C[n,k]
时间效率分析
基本操作:加法
Warshall算法
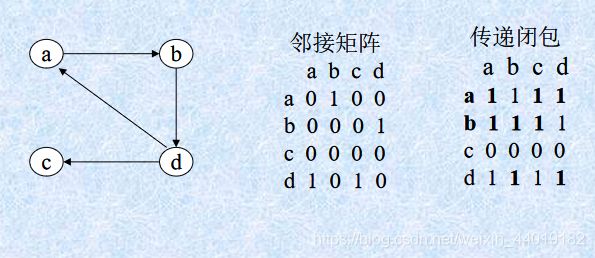
- Warshall 算法用于计算有向图传递闭包
定义
一个n顶点有向图的传递闭包可以定义为一个n阶布尔矩阵T={tij},如果从第i个到顶点到第j个顶点之间存在一条有效的有向路径,矩阵第i行(1≤i≤n)第j列(1≤j≤n)的元素为1;否则,tij为 0
-
Warshall算法思想:通过一系列n阶布尔矩阵来构造一个给定的n个顶点有向图的传递闭包:
R(0), …, R(k-1), R(k) , …, R(n)如何从R(k-1)得到R(k)?
R(k) : rij(k) = 1 , 当且仅当
存在从 i 到 j的边; 或
存在经过顶点1的从 i到 j的边; 或
存在经过顶点1和(或)2的从i 到 j的边; 或
…
存在经过顶点1和(或)2和(或)…和(或)k的从 i到 j的边
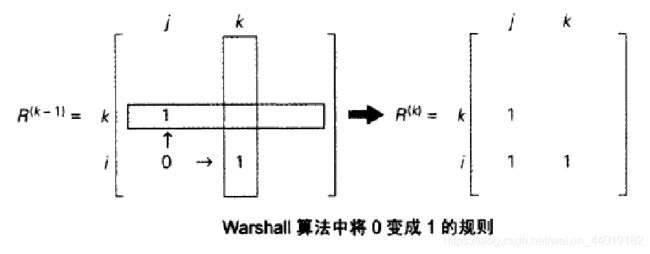
从R(k-1)得到R(k)的规则为
如果一个元素rij在R(k-1)中是1,它在R(k)中仍然是1
如果一个元素rij在R(k-1)中是0,当且仅当矩阵R(k-1)中第i行第k列的元素和第k行第j列的元素都是1,该元素在R(k)中才能变成1
Floyd算法
完全最短路径问题:找到从每个顶点到其他所有顶点之间的距离(最短路径的长度)
Floyd算法思想:通过一系列n阶矩阵来计算一个n顶点加权图的距离矩阵

矩阵D(k)的第i行第j列的元素dij (k)等于从第i个顶点到第j个顶点之间所有路径中一条最短路径的长度,并且路径的每一个中间顶点(如果有的话)的编号不大于k 。
可得递推式
最优二叉查找树
最优二叉查找树:它在查找中的平均键值比较次数是最低的(已知集合中元素的查找概率)
例:考虑分别以概率0.1,0.2,0.4,0.3来查找4个键A,B,C,D, 已下是两个非最优二叉查找树的例子
二叉查找树(Binary Search Tree)
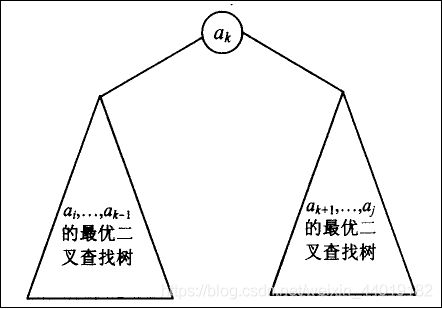
设a1,……an是从小到大排列的互不相等的键,p1,……pn是它们的查找概率。Tij是由键ai,……aj构成的二叉树,C[i,j]是在这棵树中成功查找的最小的平均查找次数,其中i,j是一些整数下标,1 ≤ i ≤ j ≤ n。
其中Tik-1 , Tk+1j 是两棵最优二叉查找子树
递推关系
注意:C[i, i-1]=0 表示空树的比较次数
C[i, i]=pi 表示单节点二叉树的比较次数
注意:C[i, i-1]=0, 表示空树的比较次数
C[i, i]=pi, 表示单节点二叉树的比较次数
我们所描述的算法是用来计算C[1,n]的,也就是最优二叉树中成功查找的平均比较次数。如果还想得到最优二叉树本身,需要维护另一个二维表来记录C[i, j]达到最小时的k值。这张表的形式和上表一样,并且也从单元R[i,j]=i(1 ≤ i ≤ n)开始,以同样的方式填充。当表格填满的时候,它的单元格指出了最优子树的根的下标,这使得我们可以对整个给定集合重新构造一棵最优树。
算法 OptimalBST(P[1..n])
// 用动态规划算法求最优二叉查找树
//输入:一个n个键的有序列表的查找概率数组P[1..n]
//输出:在最优BST中成功查找的平均比较次数,以及最优BST中子树的根表R
for i←1 to n do
C[i,i-1]←0
C[i,i]←P[i]
R[i,i]←i
C[n+1,n]←0
for d←1 to n-1 do //对角线计数
for i←1 to n-d do
j←i+d
minval←∞
for k←i to j do
if C[i,k-1]+C[k+1,j] < minval
minval←C[i,k-1]+C[k+1,j];kmin←k
R[i,j]←k
sum←P[i]; for s←i+1 to j do sum←sum+P[s]
C[i,j]←minval + sum
Return C[1,n],R
背包问题
背包问题:给定n个重量为w1,….wn、价值为vl,……,vn的物品和—个承重量为W的背包,求这些物品中最有价值的一个子集,并且要能够装到背包中
递推关系:
- 考虑一个由前i个物品(1≤i≤n)定义的实例,物品的重量分别为w1,…,wi、价价值分别为v1,…,vi,背包的承重量为j (1≤j≤W)。设V[I,j]为该实例的最优解的物品总价值
- 分成两类子集:
- 根据定义,在不包括第i个物品的子集中,最优子集的价值是V[i-1,j]
- 在包括第i个物品的子集中(因此,j-w≥0),最优子集是由该物品和前i-1个物品中能够放进承重量为 i wj的背包的最优子集组成。这种最忧子集的总价值等于vi+V[i-1,j-wi]
- 从而得到递推式
记忆功能
以记忆功能为基础的算法:用自顶向下的方式对给定的问题求解,另外维护一个类似自底向上动态规划算法使用的表格
算法 MFKnapsack(I,j)
//对背包问题实现记忆功能方法
//输入:一个非负整数f指出先考虑的物品数量,一个非负整数J指出了背包的承重量
//输出:前i个物品的最伏可行子集的价值
//注意:我们把输入数组 Weights[1…n],Values[1…n]和表格V[0..n,0..W]作为全局变量,除了行0和列0用0初始化以外,V的所有单元都用-1做初始化。
if V[I,j]<01
if j<Weights[i]
valueMFKnapsack(i-1,j)
else
valuemax(MFKnapsack(i-1),j),
Value[i]+MFKnapsack(i-1,j-Weights[i]))
V[I,j]value
return V[I,j]