暴力枚举法总结
#一 简单枚举
对于这道题目,枚举没必要从a到j都枚举一遍,因为已经知道n了,所以根据fghij的值可以求出abcde的值,这样的话枚举次数就少了很多,所以枚举也是需要思考的枚举.
import java.util.Arrays;
public class Test14 {
public static void main(String[] args) {
int n = 62;
int f,g,h,i,j;
for (f = 0; f < 10; f++) {
for (g = 0; g < 10; g++) {
if (g == f) {
continue;
}
for (h = 0; h < 10; h++) {
if (h ==g || h == f) {
continue;
}
for (i = 0; i < 10; i++) {
if (i == h|| i == g || i == f) {
continue;
}
for (j = 0; j < 10; j++) {
if (j == i || j == h|| j == g || j==f) {
continue;
}
int dvisor = f*10000+g*1000+h*100+i*10+j;
int dividend = dvisor*n;
//判断是否符合
if (dividend > 99999) {
continue;
}
isCheck(dvisor, dividend);//判断是否符合
}
}
}
}
}
}
private static boolean isCheck(int dvisor,int dividend){
String temp1 = String.valueOf(dvisor);
String temp2 = String.valueOf(dividend);
if (temp1.length() == 4) {//不够5位的前面补0
temp1 = "0"+temp1;
}
if (temp2.length() == 4) {
temp2 = "0"+temp2;
}
String str = temp1+temp2;
char[] arr = str.toCharArray();
Arrays.sort(arr);
for (int i = 0; i < arr.length; i++) {//通过字符数组来进行比较
if (arr[i] != '0'+i) {
return false;
}
}
return true;
}
}
对于这道题,因为是连续的子序列,所以枚举只需要考虑起点和终点位置.
public class Test15 {
public static void main(String[] args) {
long max = 0;
int n = 5;
long[] arr = {2,5,-1,2,-1};
//两个循环嵌套,正好对应着起点和终点
for (int i = 0; i < arr.length; i++) {
long sum = 1;
for (int j = i; j < arr.length; j++) {
sum = sum * arr[j];
if (max < sum) {
max = sum;
}
}
}
System.out.println(max);
}
}
这道题最大的疑问就是没给范围,所以需要自己来找出枚举的范围,由题目可知,1/x <= 1/y,所以替换题目中的等式,也就是2k>=y,所以y的范围就是1-2k之间,同理根据第一题的经验,可以通过k来求出x的值.
public class Test16 {
public static void main(String[] args) {
int k = 12;
for (int y = 1; y <= 2*k; y++) {
if (y != k) {
int x = k*y/(y-k);
if (x>=y) {//根据条件判断
if (x*y == (k*y + k*x)) {//这里排除小数情况
System.out.println("1/"+k+"=1/"+x+"+1/"+y);
}
}
}
}
}
}
直接暴力从S+1开始判断,这里需要了解Java中进制转换函数,都在Integer这个类中.
public class Test17 {
public static void main(String[] args) {
int n = 1600000;
for (int i = n+1; i < 10000000; i++) {
if (isCheck(i)) {
break;
}
}
}
private static boolean isCheck(int num){
int ischeck = 0;
for (int i = 2; i < 11; i++) {
String str = Integer.toString(num,i);//十进制转换为任意进制类型
// String str = Integer.parseInt(s, radix);//字符串转换为任意进制类型
StringBuilder builder = new StringBuilder(str);
if (builder.reverse().toString().equals(str)) {
ischeck++;
if (ischeck == 2) {
System.out.println(num);
return true;
}
}
}
return false;
}
}
#二.枚举排列
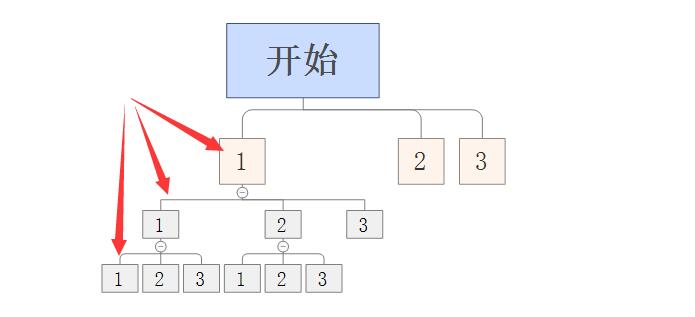
全排列问题,如果是已经知道长度的话,最好直接用循环嵌套,简单效率高,对于不知道长度的就需要递归来解决了,本质和循环嵌套差不多,相当于多个for循环轮流扫输入的数
全排列问题本身就可以理解为字典树那种形式,一个一个遍历
import java.util.Arrays;
public class Test18 {
public static void main(String[] args) {
int n = 3;
int[] A = new int[3];
printPermutation(n, A, 0);
}
/**
* 循环找到序列
* @param n 输入的n,也就是数组A的长度
* @param A 小于n的所有数
* @param cur 当前循环到的位置
*/
private static void printPermutation(int n,int[] A,int cur){
//递归边界
if (cur == n) {
System.out.println(Arrays.toString(A));
}else {
//开始填充
for (int i = 1; i <= A.length; i++) {
//先判断该数有没有在A中已经填过
boolean ischeck = true;
//用cur来控制检查次数
for (int j = 0; j < cur; j++) {
if (A[j]==i) {
ischeck = false;
break;
}
}
if (ischeck) {//如果可以填充
A[cur] = i;
//递归到下一个位置,这样就保证每个位置下都能取到所有的值
printPermutation(n, A, cur+1);
}
}
}
}
}
##2.可重集的排列
接着上一题,把题目改为输入一个数组p,你要对这个p数组中的元素进行全排列,p数组本身是可以有重复的元素的,所以要想办法去掉重复的元素排列,例如p=[1,1,1],此时输出结果只有一个1,1,1而不是27个重复的1,1,1
去重的方法是先对p进行排列,当p[i]!=p[i-1]的时候再进行递归.同时其他代码也需要修改,枚举元素换成了p,所以赋值的语句需要一定修改,具体看代码吧
import java.util.Arrays;
public class Test19 {
public static void main(String[] args) {
int[] p = {1,1,1};
int[] A = new int[p.length];
Arrays.sort(p);
printPermutation(p, A, 0);
}
/**
* 循环找到序列
* @param n 输入的n,也就是数组A的长度
* @param A 小于n的所有数
* @param cur 当前循环到的位置
*/
private static void printPermutation(int[] p,int[] A,int cur){
//递归边界
if (cur == p.length) {
System.out.println(Arrays.toString(A));
}else {
//开始填充
for (int i = 0; i < A.length; i++) {
//首先去重,因为已经排序过了,所以只需要检查当前位和其之前的位
if (i==0 || p[i] != p[i-1]) {
//先判断该数有没有在A中已经填过
int c1 = 0;
int c2 = 0;
//用cur来控制检查次数
for (int j = 0; j < p.length; j++) {
if (p[j] == p[i]) {
c1++;
}
}
for (int j = 0; j < cur; j++) {
if (A[j] == p[i]) {
c2++;
}
}
if (c2 < c1) {//如果可以填充
A[cur] = p[i];
//递归到下一个位置,这样就保证每个位置下都能取到所有的值
printPermutation(p, A, cur+1);
}
}
}
}
}
}
##3.子集生成
这样的话,只需要枚举二进制对应的序列,1,10,11…..
这里需要注意,1和10在显示的时候是一致的序列,所以当以0结尾的话,都会重复的
public class Test20 {
public static void main(String[] args) {
int[] A = {1,2,3,4};
for (int i = 1; i < 1<##4.回溯法
所谓的回溯,也就是说当发现情况已经不符合想要的那种就终止递归,返回上一层调用,这个过程成为回溯,回溯的目的是减少不必要的递归,增加程序性能