UPC 2020年春混合个人训练第十九场

问题 A: 新的世界
时间限制: 1 Sec 内存限制: 128 MB

题目描述
小学五六年级的乔猫是一个喜欢不务正业写游戏的孩纸……他曾经模仿著名的沙盒游戏《Minecraft》做过一个自己的游戏“NEWorld”。这两个游戏有着相同的规则，都是通过在一个满是方块组成的3D世界中，放置不同的方块来建造各种各样的东西。对了，游戏中还有一个独特的“近似全局光照”的亮度系统……为了简单，我们只考虑二维的情况吧。
在一个N行M列的网格中，第i行j列的格子有一个可变的“亮度” Lij（初始时都为0）和一个固定的“不透光度”Aij。现在在r行c列放入一个亮度为l的光源，NEWorld游戏引擎会根据以下逻辑，让光源逐步“照亮”附近的方格：
先将光源所在方格的亮度Lrc赋值为l。而对于i行j列一个不是光源的方格，它的亮度由Aij和四周方格的亮度所确定。定义F(i,j)=max{Li-1,j,Li+1,j,Li,j-1,Li,j+1,Aij}-Aij（此处当1≤i’≤N不成立或1≤j’≤M不成立时，Li’j’被看作是0），我们称方格(i,j)的亮度 Lij是“有效”的，当且仅当 Lij=F(i,j)。显然初始时所有亮度都是“有效”的，而放入光源后则可能存在亮度“无效”的方格。
现在引擎会循环执行操作，每一步找出当前所有亮度“无效”（不包括光源）的方格中，行数i最小的那一个（如果有多个行数i最小的，就选择其中列数j最小的方格），然后计算F(i,j)的值，将其赋值给Lij。操作会不停地执行，直到所有亮度都“有效”为止（请参考样例，循环一定会在有限步操作后结束）。请问最后p行q列的方格亮度值Lpq是多少？
注：max{a,b,c,d,e}表示取a,b,c,d,e中最大的值。

输入
第一行两个正整数N,M，表示网格大小为N行M列。
接下来的N行，每行M个正整数，其中第i行j列的正整数为Aij。
最后一行包含五个正整数r,c,l,p,q，表示在r行c列放入亮度为l的光源，需要查询的是亮度计算完成后p行q列的亮度值。

输出
包含一行一个正整数，表示最后Lpq的值。
样例输入 Copy
4 4
1 1 1 1
1 4 4 1
1 1 4 1
1 1 1 1
3 2 4 1 1
样例输出 Copy
1
提示
这张图展示了亮度重新计算的过程。数字表示方格亮度Lij，白色方格为光源，灰色方格的灰度表示该方格的不透光度Aij（浅灰为1深灰为4），绿色方格是亮度“无效”的方格，其中深绿色是即将被重新计算亮度的方格。

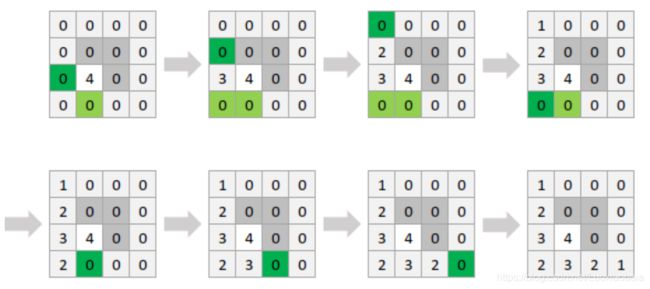
对于60% 的数据：N,M≤100。
对于100% 的数据：N,M≤500，1≤Aij,l≤109，1≤r,p≤N，1≤c,q≤M。

猜测出题人的本意是让我们用 Dijkstra 来做，然鹅，剑走偏锋…

// A: 新的世界 (DFS+SPFA)

#include
using namespace std;

#define in inline
#define re register
#define rep(i,a,b) for(re int i=a;i<=b;i++)
#define repd(i,a,b) for(re int i=a;i>=b;i--)
#define For(i,a,b) for(re int i=a;i
#define _(d) while(d(isdigit(ch=getchar())))

template<class T>in void g(T&t)
{
    T x,f=1;
    char ch;
    _(!)ch=='-'?f=-1:f;
    x=ch-48;
    _()x=x*10+ch-48;
    t=f*x;
}

const int N=504;
int a[N][N],c[N][N],n,m,R,C;
bool vis[N][N];
typedef pair<int,int>P;
typedef pair<int,P>PP;
priority_queue<PP>q;

#define mk(a,b) make_pair(a,b)
#define fi first
#define se second

const int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};

in void bfs()
{
	priority_queue<PP>q;
	q.push(mk(0,mk(R,C)));
	while(!q.empty())
	{
		PP now=q.top();
		q.pop();
		P tt=now.se;
		int x=tt.fi,y=tt.se;
		if(vis[x][y]) continue;
		vis[x][y]=1;
		For(i,0,4)
		{
			int tx=x+dx[i],ty=y+dy[i];
			if(tx>n||tx<1||ty>m||ty<1) continue;
			if(c[tx][ty]<c[x][y]-a[tx][ty])
			{
				c[tx][ty]=c[x][y]-a[tx][ty];
				q.push(mk(c[tx][ty],mk(tx,ty)));
			}
		}
	}
}

int main()
{
	g(n),g(m);
	rep(i,1,n) rep(j,1,m) g(a[i][j]);
	g(R),g(C);
	g(c[R][C]);
	bfs();
	int ax,ay;
	g(ax),g(ay);
	
	/*rep(i,1,n){
		rep(j,1,m) cout<
	printf("%d\n",c[ax][ay]);
	return 0;
}

问题 D: 扫雷游戏
时间限制: 1 Sec 内存限制: 128 MB

题目描述
Geobiyye是个喜欢玩扫雷的女孩子。
现在Geobiyye给了你一个n行m列的雷区，并且告诉你每个格子是否有雷，她想要知道每一个非地雷格中的数字应该是多少。
一个非地雷格中的数字应是与它相邻的8个格子（边角不足8个）所含有的地雷的数目。
由于Geobiyye沉迷于玩扫雷，于是她将问题抛给了你。

输入
第一行2个正整数n,m，分别表示雷区的行数和列数。
接下来n行，每行m个字符，字符’#‘表示相应格子是地雷，字符’?'表示相应格子不是地雷。

输出
输出包括n行，每行m个字符。若相应格子是地雷，你应该输出字符’#’，否则你应该输出一个正整数表示该格子周围的地雷数。
样例输入 Copy
3 3
#??
???
?#?
样例输出 Copy
#10
221
1#1
提示
对于100%的数据：n,m≤100。

出现不少次了，这次小白直接记录、判断、输出来写了。

// D.扫雷游戏 

#include 
using namespace std;

int main()
{
	int sn,sm,i,j,m[1003][1003];
	cin>>sn>>sm;
	char a[1003][1003];
	
	for(i=1;i<=sn;i++)  scanf("%s",a[i]);
	
	for(i=1;i<=sn;i++)
	{
		for(j=0;j<sm;j++)
		{
	    	if(a[i][j]=='#')
			{
	    		m[i-1][j-1]++;
	    		m[i][j-1]++;
	    		m[i+1][j-1]++;
	    		m[i-1][j]++;
	    		m[i+1][j]++;
	    		m[i-1][j+1]++;
	    		m[i][j+1]++;
	    		m[i+1][j+1]++;
			}
		}
	}
	
	for(i=1;i<=sn;i++)
	{
        for(j=0;j<sm;j++)
		{
            if(a[i][j]=='#')   cout<<"#";
            else cout<<m[i][j];
        }
        cout<<endl;
    }
    
	return 0;
}

问题 E: 音乐
时间限制: 1 Sec 内存限制: 128 MB

题目描述
Geobiyye是一个喜欢听音乐的女孩子。
Geobiyye有 段喜欢的旋律，每段旋律可以用一个仅由小写字母构成的字符串表示。每段旋律有一个愉悦值w，表示Geobiyye对这段旋律的喜爱程度。
一首歌曲也可以用一个仅由小写字母构成的字符串表示。定义一段旋律在一首歌曲中的价值为w×cnt，其中cnt表示这段旋律在歌曲中的出现次数。定义Geobiyye对于一首歌曲的喜爱程度为Geobiyye所有喜欢的旋律的价值之和。
现在Geobiyye想知道自己对一首歌曲的喜爱程度是多少。

输入
第一行一个正整数n，含义见题目描述。
接下来n行，每行一个字符串ai和一个正整数wi，分别表示Geobiyye喜欢的一段旋律和这段旋律的愉悦值。
最后一行一个字符串S，表示一首歌曲。

输出
一行一个正整数，表示Geobiyye对这首歌曲的喜爱程度。
样例输入 Copy
3
ana 2
a 3
ba 1
banana
样例输出 Copy
14
提示
样例解释：
第一段旋律ana在歌曲中出现了2次，价值为22=4；
第二段旋律a在歌曲中出现了3次，价值为33=9；
第三段旋律ba在歌曲中出现了1次，价值为1*1=1；
喜爱程度为4+9+1=14。

【数据范围】
对于100%的数据：n≤10，|S|≤100，Σ|ai|≤100,1≤w≤100。
其中|S|表示字符串S的长度。

题解：定义一个 string数组,表示有多个子串要输入，每个子串对应输入各自的愉悦值，查找每一个子串出现的次数，与对应的愉悦值相乘即为每个的价值，将之累加。

// E.字符串子串的查找

#include 
#define ll long long 
using namespace std;

int main()
{
	string s[1010],s1; 
	int n,a[1010],sum=0;
	cin>>n;
	for(int i=1;i<=n;i++) cin>>s[i]>>a[i];
	cin>>s1;
	for(int i=1;i<=n;i++)
	{
		int weizhi=0,count=0;
        while(1)
        {
            weizhi = s1.find(s[i],weizhi);
            weizhi++;
            if(0==weizhi)    break;
            else    count++;    
        }
        sum+=count*a[i];
	}
	cout<<sum;
	return 0;
}

问题 F: 切西瓜
时间限制: 1 Sec 内存限制: 128 MB

题目描述
LHY和他的小伙伴们有一个西瓜，他们想要吃西瓜。
但LHY的小伙伴们太多了，因此一个人独吞整个西瓜会被认为是不道德的。
在ob的帮助下，LHY获得了一把没有厚度而锋利的西瓜刀，他每次能用这把刀把西瓜完整而不弯曲地切一刀。假如LHY刀法很好，能把西瓜切得足够薄，他想知道这样切孮刀以后，最多能有多少西瓜馕。
输入
一行一个整数n，表示切的次数。
输出
一行一个整数，表示最多能切出多少西瓜馕。
样例输入 Copy
2
样例输出 Copy
4
提示
样例解释

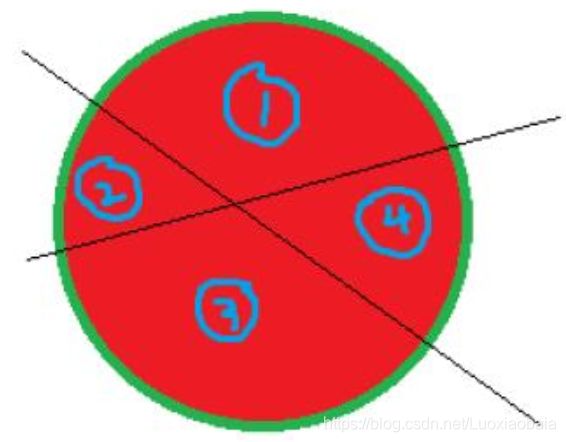
对于30%的数据满足n≤3。
对于另外40%的数据满足n≤500。
对于另外30%的数据满足n≤1,000,000,000。

题解：第一刀可以把它切成2块，然后第二刀成4块，第三刀成7块，第四刀成11块，第五刀成16块 第一刀可随便切，切成2块 第二刀只要与第一刀的切痕相交，即可切出4块，否则，只能切出3块 第三刀要与前面两刀的切痕相交，且不能通过前面两条切痕的交点和切痕的端点，这样可切出7块 … 若想第N 刀能切出最多的块数，需使这一刀的切痕与前面的 N-1个切痕都相交，并且不能通过切痕的交点和端点。第 N 刀把其与前 N-1刀切痕相交的 N-1 半段切痕相邻的N部分一分为二 我们设数列﹛an﹜来表示切出块数 a1=2，表示第一刀能分两块 则根据 “第 N 刀把其与前 N-1 刀切痕相交的 N-1 半段切痕相邻的 N 部分一分为二” 可得出递推式： a[n] = a[n-1]+n ，可归纳出通项公式：a[n] = (n*n+n+2)/2。

// F.找规律 +归纳通项公式 
 
#include 
#define ll long long 
using namespace std;

ll n,ansa;

int main()
{
	scanf("%lld",&n);
	ansa=(n*n+n+2)/2;
	cout<<ansa;
	return 0;
}

问题 G: 玩游戏
时间限制: 1 Sec 内存限制: 128 MB

题目描述
LHY有一个机器人。它正在进行测试。
机器人现站在n行m列网格中的某一个格子里，我们用字母a来表示它的位置。在接下来的测试中，LHY会给它发送一个字符串，表示机器人将要行进的路线。
机器人将会一个字符一个字符地扫描字符串，而字符串中每一个字符都有特定的含义：
• a:向左移动一个格子。
• d:向右移动一个格子。
• w:向上移动一个格子。
• s:向下移动一个格子。
当然，机器人也有自我保护措施。如果它面前有障碍，或者要越过整张网格了，它就会在这一步停止移动。
同时，LHY也设定了一个终点b。现在他想知道机器人最后会经过多少个格子（包括机器人的起点和终点），以及它会不会走过终点b。
输入
第一行两个数n，m，分别表示矩形的行数和列数。
接下来n行，每行m个字符，具体内容参考题目描述。
输出
第一行一个整数，表示总共经过了多少格子。
第二行YES或NO，表示经过了终点或没有经过终点。
样例输入 Copy
8 8
.a…
.…
….
…
…
…b..
…
…
asssssdddd
样例输出 Copy
11
YES
提示
样例解释：
用加号来表示机器人的路线。

100%的数据满足n≤2000,m≤2000;操作数不超过5000。

暂时还没有AC，感觉是单人游戏的SG函数，有机会补上。